2538

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования

«Нижегородский государственный архитектурно-строительный университет»

В.В. Драгунова , Г.П. Опалева , Л.С. Сенниковская

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Учебно-методическое пособие по подготовке к лекционным и практическим занятиям

по дисциплине «Математика» для обучающихся по направлению подготовки 20.03.01_Техносферная безопасность, профиль Безопасность технологических процессов

Нижний Новгород

2016

0

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования

«Нижегородский государственный архитектурно-строительный университет»

В.В. Драгунова , Г.П. Опалева , Л.С. Сенниковская

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Учебно-методическое пособие по подготовке к лекционным и практическим занятиям

по дисциплине«Математика» для обучающихся по направлению подготовки 20.03.01_Техносферная безопасность, профиль Безопасность технологических процессов

Нижний Новгород ННГАСУ

2016

1

УДК 517.9

Драгунова В.В. Определенный интеграл [Электронный ресурс]: учеб.-метод. пос. / В.В. Драгунова , Г.П. Опалева , Л.С. Сенниковская; Нижегор. гос. архитектур. - строит. ун - т – Н. Новгород: ННГАСУ, 2016. – 48 с;ил. 1 электрон. опт. диск (CD-RW)

В пособии приводятся необходимые формулы, подробно разбираются решения типовых задач, предоставляются задачи для самостоятельного решения.

Предназначено обучающимся в ННГАСУ при изучении раздела «Определенный интеграл» курса высшей математики по направлению подготовки 20.03.01_Техносферная безопасность, профиль Безопасность технологических процессов

т

©В.В. Драгунова , Г.П. Опалева , Л.С. Сенниковская, 2016

©ННГАСУ, 2016

2

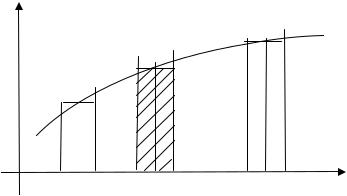
1. Понятие определенного интеграла

Пусть на отрезке [a,b] определена непрерывная функ-

ция y=f(x):

y

•

•

число, получаемое следующим образом:

1)промежуток [a,b] разбивается на n элементарных

2)внутри каждого элементарного промежутка выби-

рается произвольная точка ξi , xi−1 ≤ ξi ≤ xi , в

каждой из которых вычисляется значение функции;

3)значения функции f (ξi ) умножаются на длины

соответствующих промежутков xi = xi − xi−1 ; 3

4)все полученные произведения f (ξi )Dxi суммиру-

ются

Sn = f (ξ1 )× Dx1 + f (ξ2 )× Dx2 + ...

n

+ f (ξn )× Dxn = ∑ f (ξi ) × D xi .

i=1

Полученная сумма называется интегральной суммой для функции f(x) на отрезке [a,b];

5)вычисляется предел полученной суммы

Если этот предел существует и не зависит от выбора xi и ξi, то он называется определенным интегралом и обозначается

b

∫ f (x)dx ,

a

где f (x) – подынтегральная функция, x - переменная интегрирования,

a и b – границыизмененияпеременной х, a ≤ x ≤ b, a – нижний предел интегрирования,

b – верхний предел интегрирования.

Таким образом

4

2. Задачи, приводящие к определенному интегралу

К операции интегрирования функции на отрезке

приводят задачи различного характера.

1. Задача о вычислении работы

Пусть под действием силы F материальная точка движется по прямой от точки x1=a до точки x2=b. Вычислим работу, производимую этой силой на заданном промежутке.

Если сила есть функция координаты х, т.е. F=F(x), непрерывная на [a,b], то разбив отрезок на n произвольных частей Dx1, Dx2 ,...Dxn и выбрав в каждом частичном

отрезке произвольную точку ξi, будем считать F(x) в пределах этого отрезка постоянной и равной F(ξi). Вычислим

работы силы F на промежутке [a,b].

Если предел этой суммы существует и не зависит от выбора точек xi и ξi, то

b

A = ∫ F (x)dx

a

2. Задача о вычислении площади криволинейной

трапеции

Пусть на плоскости хОу дана фигура, ограниченная отрезком [a,b] оси Ох, прямыми x=a, x=b и графиком непрерывной и неотрицательной функции y=f (x) на [a,b]. Такую фигуру называют криволинейной трапецией.

5

у

Рис.2.

Вычислим площадь этой криволинейной трапеции. Разобьем промежуток [a,b] на n элементарных промежутков, тогда площадь прямоугольника, построенного на Dxi = xi - xi−1 , равна Si = f (ξi )× Dxi , где xi−1 £ ξi £ xi . А приближенное значение площади S под кривой равно суммарной площади этих прямоугольников

Точное значение площади получим, вычислив

Таким образом:

b

S = ∫ f (x) dx

6

π

Пример № 2. Вычислить ∫(2x +1) ×cos x dx . 2

0

Так как подынтегральная функция представлена в виде произведения степенной функции (2х +1) и тригономет-

рической cos x , то полагая

2

где f (x) - непрерывная функция, a ≤ x ≤ b ,

x=φ(t) - монотонная функция, имеющая непрерывную производную, dx = ϕ ′(t)dt, α ≤ t ≤ β , где φ(α) =а и ϕ (β ) = b .

8

4.Несобственные интегралы

4.1.Интегралы с бесконечными пределами

Если функция f (x) определена и непрерывна на промежутке [a, ∞), то по определению:

+∞ b

∫ f (x) dx = blim→∞ ∫ f (x) dx .

a a

Если существует конечный предел, то интеграл называют сходящимся, если предел бесконечный или не суще-

ствует, то - расходящимся.

9