
2532
.pdf
5.3.1. Если плоская кривая АВ задана уравнением y = f (x) , где f (x) – непрерывная на [a,b] функция, то длина дуги выражается формулой
хB |
|
||
L = ∫ |
1 + (y′)2 |
dx |
(12) |
хA |
|
||
Тогда площадь поверхности, образованной вращением этой дуги АВ вокруг оси Ох вычисляется по формуле:
хB |
|
||
Px = 2π ∫ y(x) |
1 + (y′)2 |
dx |
(13) |
хA |
|
||
Если поверхность получается вращением дуги АВ, заданной уравнением x = ϕ ( y) вокруг оси Оу, то применяется формула:
уB |
|
Py = 2π ∫ x(y) 1 + (x′)2 dy |
(14) |
уA
5.3.2.Если кривая АВ задана параметрическими
уравнениями x= x (t), |
y= y (t), то длина дуги выражает- |
|||
ся формулой |
|
|
|
|
|
|
|
|
|
|
tB |
|
|
|
|
L = ∫ |
(xt′ )2 + (yt′ )2 dt |
(15) |
|
|
t A |
|
|
|
|
|
|
|
|
|
|
20 |
|
|
5.3.3. При вычислении длины дуги в случае, когда кривая АВ задана в полярных координатах уравнением ρ = ρ (φ), тогда формула принимает вид:
ϕB |
|
||
L = ∫ |
ρ 2 (ϕ) + ρ ′2 (ϕ) |
dϕ |
(16) |
ϕ A |
|
||
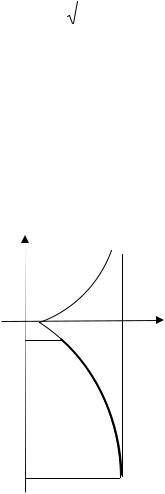
Задача № 4 Вычислить длину дуги полукубической параболы y2 = (x −1)3 , заключенной между точками А (2,-1)
и В (5,-8).
у
-1 |
• |
׀ |
׀ ׀ ׀ ׀ |
5 |
х |
|
– |
1 |
А• |
2 |
|
||
|
– |
|
|
|
|
|
|
– |
|
|
|
|
|
|
– |
|
|
|
|
|
|
– |
|
|
|
|
|
|
– |
|
|
|
|
|
|
– |
|
|
|
|
|
-8 |
– |
|
|
• |
В |
|
Рис.13.
Решение: Выразим из уравнения кривой у:
21

3
у = ±(х −1)2 .
Функция у (х) определена для x ≥ 1. Поскольку данные точки лежат в четвертой четверти, то
3
y = − (x −1) 2 .
Отсюда
1
у′ = − 3 (х −1)2 . 2
Подставляя в формулу (12) у′ , хА = 2, хВ = 5, получим
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
(x |
− 1) dx |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
9 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
LAB = ∫ 1 + |
|
= |
∫ 9x − 5 dx |
= |
|||||||||||||||||||||||||||
4 |
|
2 |
|||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
5 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
5 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
1 |
|
∫(9x − 5)2 d (9x − 5) = |
1 |
(9x − 5)2 |
|
= |
||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
18 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
− 13 |
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
40 |
40 |
13 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
|
|
|
40 2 |
− 13 2 |
= |
|
|
|
|
|
|
|
|
|
|
|
≈ 7,63 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
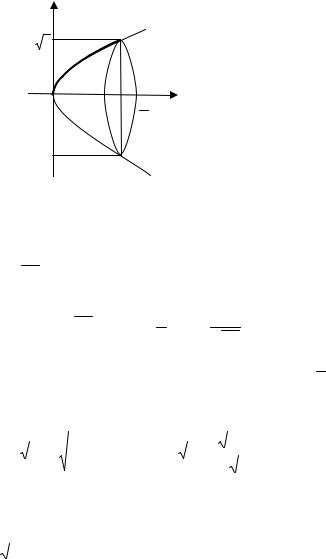
Задача № 5 Найти площадь поверхности, образован-
ной вращением вокруг оси Ох дуги параболы у2 = 2х, заключенной между ее вершиной и точкой пересечения с пря-
мой 2х = 3.
Решение: Построим линии в системе координат хОу
(рис.14).
22
у
|
|
В |
3 |
|
• |
– |
|
|
А |
|
|
0• |
׀ |
3 х |
|
||
– |
|
2 |
Рис. 14
Искомая площадь поверхности образована вращением дуги АВ параболы вокруг оси ох. Из уравнения у2 = 2х
находим у = ±
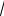 2х . Поскольку дуга АВ лежит в первой четверти, то
2х . Поскольку дуга АВ лежит в первой четверти, то
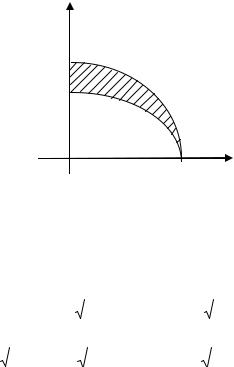
y = 
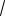 2x , 0 £ x £ 3 , y¢ = 1 . 2
2x , 0 £ x £ 3 , y¢ = 1 . 2 
 2x
2x
Подставляя у и у' в формулу (13), при хА = 0, хВ = 3 2
получим
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
|
|
|
|
2 |
x + |
1 |
|
||||||||||||||
Px = 2π ∫ |
|
× 1 + |
|
|
dx = 2π ∫ |
|
× |
|
dx = |
||||||||||||||||||
2x |
2x |
||||||||||||||||||||||||||
|
2x |
|
|
|
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= 2π ∫ |
|
dx = |
∫(2x + 1) 2 d (2x + 1) = |
||||||||||||||||||||||||
2x + 1 |
|||||||||||||||||||||||||||
2 |
|
||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
23
|
(2x + 1) |
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|||||
|
|
|
|
2π |
|
|
|
14 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
2 |
|
|
||||||||
= 2π |
|
|
|
|
|
|
= |
|
|
4 |
|
− 1 |
= |
|
|
π . |
3 |
|
|
|
|
|
3 |
|
3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
5.4. Статические моменты. Центр тяжести
Для плоской фигуры, ограниченной кривыми
y = f1 (x) , y = f2 (x) ( f1 (x) ≤ f2 (x))
и прямыми
х= а, x=b (a ≤ x ≤ b),
ипредполагая, что по этой фигуре равномерно распределена масса так, что её поверхностная плотность ρ постоянна и для простоты положим её равной единице (ρ = 1), тогда масса фигуры будет измеряться её площадью.
Тогда статические моменты относительно координатных осей Ох и Оу выражаются формулами
|
|
|
b |
|
|
|
M x = |
1 |
∫(f22 (x) − f12 (x))dx |
; |
(17) |
2 |
|||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
M y = ∫ x( f2 (x) − f1 (x))dx |
. |
(18) |
||
|
|
a |
|
|
|
|
|
|
|
|
|
Центр тяжести плоской фигуры имеет координаты
xc |
= |
M y |
, yc = |
M |
x |
|
, |
(19) |
|
|
|
||||||
S |
S |
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
где S - площадь фигуры.
24
Задача № 6. Найти центр тяжести фигуры, ограни-
ченной эллипсом 4х2 + 9 у2 = 36 и окружностью x2 + y 2 = 9 и расположенной в первом квадранте.
Решение: Построим фигуру, ограниченную указанными линиями (рис.15).
у |
|
3 – |
x2 + y2 = 9 |
2 –
– 4x2 + 9y2 = 36
׀ |
׀ |
׀ |
|
0 |
|
3 |
х |
Рис.15.
Вычислим сначала статические моменты. Из уравнений окружности и эллипса имеем
|
|
|
|
|
|
|
|
(x) = |
|
|
|
|
, f1 (x) = |
2 |
|
|
|
, |
|||||||||||||
|
|
|
|
|
f2 |
9 − x2 |
9 − x2 |
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||
|
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
M y = ∫ x 9 |
− x |
|
− |
|
|
|
9 − x |
|
|
|
dx |
= |
|
|
|
∫ x 9 − x |
|
dx = |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
0 |
|
|
|
|
|
|
|
||||
|
|
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
= − |
1 |
∫(9 − x2 )2 |
d (9 − x2 )= − |
(9 − x2 )2 |
|
3 = 3, |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
6 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|||
M x |
= |
1 |
∫ |
(9 - x2 )- |
4 |
(9 - x2 ) dx = |
1 |
× |
5 |
× ∫(9 - x2 )dx = |
||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
0 |
|
|
9 |
|
2 9 0 |
|||||
|
5 |
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||
= |
|
|
|
|
9x - |
|
|
=5. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
|
18 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||
Площадь четверти круга радиуса R = 3 равна 9π , а 4
площадь четверти эллипса с полуосями а = 3 и b = 2 вычислим по формуле (6):
3 |
3 |
Sэл = ∫ 23 
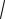 9 - x2 dx = 23 ∫
9 - x2 dx = 23 ∫
 9 - x2 dx =
9 - x2 dx =
0 0
|
2 |
x |
|
|
|
|
9 |
|
x |
|
3 |
|
3 |
π . |
|
|
|
|
2 |
|
|
||||||||||
= |
|
|
|
|
9 - x |
|
+ |
|
arcsin |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|||||||||
|
3 |
2 |
|
|
|
|
2 |
3 |
|
0 |
|
2 |
|
||
Поэтому площадь рассматриваемой фигуры равна
S = Sокр - Sэл = 9π - 3π = 3π . 4 2 4
Таким образом,
xc |
= |
M y |
= |
4 |
; |
yc = |
M |
x |
= |
20 |
. |
S |
π |
S |
|
3π |
|||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
26 |
|
|
|
|
|

Задание № 1
Вычислить определенные интегралы:
π
4
1.01. ∫ x tg 2 2x dx
0
π
4
1.02. ∫ x cos2 2x dx
0
1
1.03. ∫ x 2e−2 x dx
0 |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
4 |
|
x dx |
|||||
1.04. ∫ |
|
||||||
|
|
|
|
|
|
||
|
sin 2 3x |
||||||
π |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
4 |
|
x dx |
|||||
1.05. ∫ |
|||||||
|
|
|
|
||||
cos2 x |
|||||||
0 |
|
|
|
|
|
|
|
е |
(1 + ln x)2 dx |
||||||
1.06. ∫ |
|||||||
1 |
|
|
|
|
|
|
|
0 |
|
− |
x |
|
|||
1.07. ∫ x2e 2 dx
−2
π
1 x2 dx
1.09. ∫ ( )2
0 1 + x2
e2
1.10. ∫ lnxx dx
1
π
1.11. ∫(π - x)×sin x dx
0
π
2
1.12. ∫(x -1)×cos x dx
0
0
1.13. ∫(2x + 3)e−x dx
−1
3 e
e
1.14. ∫ x2 ln x dx
1
a
1.15. ∫ x2 ln(x + a)dx
0
2 |
x cos x |
|
2 |
|
|
1.16. ∫(x + 2)ln(x + 3)dx |
|||
1.08. ∫ |
|
|
dx |
|
sin3 |
x |
|||
π |
|
|
|
−2 |
4 |
|
|
|
|
|
|
|
|
27 |

2 |
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
|||||
1.17. ∫ x ln 1 |
+ |
|
|
dx |
||||||
|
|
|||||||||
1 |
|
|
|
|
х |
|
||||
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
1.18. ∫ x2 2− x dx |
|
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
x arcsin x |
|
|
|
|||||
1.19. ∫ |
|
|
|
|
|
|
dx |
|||
|
|
|
|
|
|
|
||||
|
|
|
3 |
|
||||||
0 |
|
|
(1 - x2 ) |
|
|
|
||||
1
1.20. ∫ x2 arctg x3dx
0
3
ln x dx
1.21. ∫2 (1- x)2
3
1.22. ∫ x2 3−x dx
1
1
1.23. ∫ln(x2 + x +1)dx
0
e−1
1.24. ∫ln(x +1)dx
0
π
∫π -
1.25.x cos 3x dx
22
0
π
∫π -
1.26.x sin 2x dx
22
0 |
|
|
|
1 |
− |
1 |
|
1.27. ∫(2x +1)×e |
|
x dx |
|
2 |
|||
0 |
|
|
|
1 |
|
|
|
1.28. ∫ x2 arctg x dx
0
2
1.29. ∫(3x -1)e2 x dx
1
π
4
1.30. ∫(x sin x)2 dx
0
28
Задание № 2
Вычислить определенные интегралы:
4
dx
2.01. ∫1+ 
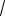 x
x
0
1
2.02. ∫
 4 - x2 dx
4 - x2 dx
0
9
 x dx
x dx
2.03. ∫ x -1
4
4
dx
2.04. ∫1+ 
 2x +1
2x +1
0
293 (x - 2)2 dx
2.05.∫3 3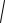 (x - 2)2 + 3
(x - 2)2 + 3
ln 2
2.06. ∫ 
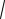 e x -1 dx
e x -1 dx
0
π
1
∫ 1 - x2
2.09. dx x2
 2
2
2
ln 5
2.10. ∫ e x e x -1 dx e x + 3
0
2 |
|
x2 |
-1 |
|
|
2.11. ∫ |
|
dx |
|||
|
x |
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
dx |
||
2.12. ∫ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2x + |
|
3x +1 |
|||
0 |
|
||||
|
|
|
|
|
|
1x2 dx
2.13.∫ (x +1)4
0 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
x3 dx |
|
|
|
2.14. ∫ |
|
|
|
||
|
|
|
|
||
|
|
2 |
|
||
0 |
3 |
(x2 +1) |
|
||
2 |
|
|
e |
|
|
|
|
|||
|
|
|
|
|
|
|||||
2.07. ∫ |
dx |
|
2.15. ∫ |
ln x × 4 1 |
+ ln x |
dx |
||||
3 + 2 cos x |
|
x |
|
|
||||||
0 |
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
π |
|
|
|
|
|
|
|
|
|
|
4 |
dx |
3 |
|
|
|
|
|
|
||
2.08. ∫ |
2.16. ∫ x2 9 - x2 dx |
|||||||||
|
||||||||||
1 + a 2 sin 2 x |
||||||||||
0 |
|
|
−3 |
|
|
|
||||
29
