
2526
.pdf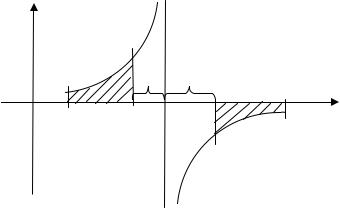
Аналогично
|
b |
|
b |
|
|
∫ |
f (x) dx = |
lim |
f (x) dx , |
|
|
a→− ∞ ∫ |
|
|
|
−∞ |
|
a |
|
тогда |
|
|
|
|
∞ |
|
c |
|
∞ |
∫ f (x) dx = ∫ f (x) dx + ∫ f (x)dx . |
||||
−∞ |
|
−∞ |
|
c |
4.2. Интегралы от неограниченных функций
Пусть функция у = f(x) определена и непрерывна во все точках промежутка [a,b], за исключением точки c [a,b], в окрестности которой она не ограничена:
lim f (x) = ∞ (см. рис.3.)
x→c
у
|
ε |
δ |
b |
|
|
с+δ |
|
а |
с-ε |
с |
х |
Рис.3
10
По определению:
b |
b−ε |
|
∫ f (x) dx = εlim→+0 ∫ f (x) dx , |
при c = b, |
|
a |
a |
|
b |
b |
|
∫ f (x) dx = δlim→+0 ∫ f (x) dx , |
при с = а, |
|
a |
a+δ |
|
b |
c−ε |
b |
∫ f (x) dx = εlim→+0 |
∫ f (x) dx + δlim→+0 ∫ f (x) dx , |
|
a |
a |
c+δ |
при a < c < b.
Если пределы, стоящие в правых частях этих формул существуют и конечны, то соответствующие интегралы называют сходящимися, в противном случае – расходящи-
мися.
+∞ |
− |
|
x |
|
|
|
Пример № 4. Вычислить ∫е |
|
|
|
|
|
|
|
3 dx . |
|
|
|||
0 |
|
|
|
|
|
|
Это несобственный интеграл с бесконечным верхним |
||||||
|
|
f (x) = е− |
x |
|
||
|
|
|
|
|||
пределом интегрирования. Функция |
|
3 |
непрерывна |
|||
на [0, + ∞).
11
+∞ − |
x |
|
|
|
|
|
|
b |
− |
x |
|
|
|
|
|
|
b |
− |
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∫е 3 dx = |
|
lim |
∫е |
3 |
dx = −3 lim |
∫ |
е 3 |
d |
− |
|
|
= |
|||||||||||||
|
|
||||||||||||||||||||||||
0 |
|
|
b→+∞ |
0 |
|
|
|
|
|
b→+∞ |
0 |
|
|
|
|
|
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
− |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
= −3 lim е |
|
3 |
|
|
= −3 lim |
|
|
|
− |
|
|
= 3. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
b→+∞ |
|
|
|
|
0 |
|
|
b→+∞ |
|
b |
|
|
е0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
е3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Предел существует, значит несобственный интеграл сходится.
|
|
|
|
|
|
|
|
|
|
|
5 |
|
dx |
|
|
|
|
|
|
|
|||
Пример № 5. Вычислить |
∫ |
|
|
|
. |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
(x − 2)7 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Подынтегральная функция |
f (x) = |
|
1 |
|
|
имеет |
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
(x − 2)7 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
разрыв при х=2, поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5 |
|
dx |
|
5 |
|
|
|
dx |
|
|
|
|
|
|
|
(x − 2)−7+1 |
|
5 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
= lim |
|
|
|
|
= |
|||||
|
|
|
|
|
|
|
|
(x − 2)7 |
|
|
|
||||||||||||
∫2 (x − 2)7 |
ε →0 2∫+ε |
|
ε →0 |
|
− 7 + 1 |
|
2+ε |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
= − |
lim |
|
|
− |
|
|
|
|
|
= ∞. |
|
|
|||||||||||
|
|
6 |
|
|
|
|
|
6 |
|
|
|
||||||||||||
|
|
|
|
(5 − 2) |
|
(2 + |
ε − 2) |
|
|
|
|
|
|
|
|||||||||
|
|
6 ε →0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Предел бесконечный, значит несобственный интеграл расходится.
12
5.Приложения определенного интеграла
5.1.Площадь плоской фигуры
5.1.1. Площадь криволинейной трапеции (рис.2),
ограниченной сверху графиком непрерывной |
функции |
||
y = f (x) ³ 0 находится по формуле |
|
||
|
|
|
|
|
b |
|
|
|
S = ∫ f (x) dx |
|
(6) |
|
a |
|
|
|
|
|
|
5.1.2. Площадь криволинейной трапеции, ограниченной сверху кривой, заданной параметрическими уравнениями
|
x = x(t) |
|
||
|
|
, t [α , β ], |
|
|
|
y = |
y(t) |
|
|
вычисляется по формуле |
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
SD = ∫ y(t) x′(t) dt . |
|
(7) |
|
|
α |
|
|
|
5.1.3. Площадь плоской фигуры, ограниченной прямыми x= a, x=b, двумя кривыми у1 = ун(х), y2 = yв(х) ( ун (х) ≤ ув (х) при всех значениях х [a, b] )
13

|
|
y |
|
|
|
|
yв (x) |
|
|
|
|
D |
|
|
a |
|
• |
b |
|
|
yн(x) |
|
|
|
|
|
Рис.4. |
|
|
вычисляется по формуле |
|
|||
|
|
|
|
|
|
|
b |
|
|
|
|
SD = ∫[yв (х) − ун (х)]dx . |
(8) |
|
|
|
a |
|
|
|
|
|
|
|
В отдельных случаях границы могут быть в точках пересечения кривых. Тогда а и b равны абсциссам точек пересечения указанных кривых.
5.1.4. Площадь криволинейного сектора, ограниченного лучами φ=α, φ = β и кривой ρ = ρ(φ)
|
|
|
|
|
|
|
|
ρ=ρ(φ) |
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β α |
|
|
|||
|
|
|
|
|
||||
|
|
|
|
|||||
|
• |
|
|
|||||
вычис- |
|
|
Рис.5. |
|
ляется |
|||
по |
|
|
|
|
|
|
|
форму- |
ле |
|
|
|
|
|
|
|
|
|
14 |
|
|
|||||
2 |
β |
|
|
|
∫ |
|
|
||
SD = |
1 |
|
ρ 2 (ϕ) dϕ |
(9) |
|
α |
|||
|
|
|
|
|
|
|
|
|
|
Задача № 1. Найти площадь фигуры, ограниченной линиями у = 4 - х2 и у = х2 - 2х.
Решение: Построим кривые (рис.6.).
|
y |
|
|
|
|
|
|
|
• 4 |
|
|
|
|
2 |
-2x |
|
|
|
|
|
|
y=x |
|
|
А• • 3 |
|
|
|
|
|
|
• |
• |
• |
1 |
• |
В |
x |
|
|
-1 |
|
|
2 |
|||
y=4 - x2
Рис.6.
Из рисунка 6 видно, что пределами интегрирования являются абсциссы точек пересечения этих кривых. Найдем их. Для этого решим систему уравнений.
y = 4 - x22
y = x - 2x,
в результате получим х1 = -1, х2 = 2 .
Так как 4 - х2 ³ х2 - 2х при − 1 ≤ х ≤ 2 , то искомая площадь S равна
15
S = ∫2 [(4 − x 2 )− (x 2 − 2x)]dx =∫2 (4 + 2х − 2х2 )dx =
|
−1 |
|
|
|
|
|
−1 |
|
|
|
x 2 |
x3 |
|
|
|
|
|
2 |
|||||
= |
4x |
+ 2 |
|
− 2 |
|
|
= 9 |
|
|
||||||
|
|
|
2 |
|
3 |
|
−1 |
|
|
|
|
|
|||
Задача № 2. Вычислить площадь, ограниченную кривой ρ = 2(1 + sin ϕ ).
Решение: Построим по данному уравнению кривую. Это будет кардиоида (рис.7.)
• 4
• |
׀ ׀ |
ρ |
0 |
2 |
Рис.7.
Так как область симметрична относительно луча ϕ = π , то
2
по формуле (9) будем иметь:
16
|
|
|
|
π |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
S = 2 × |
1 |
× ∫ |
[2 |
(1 + sin ϕ )]2 dϕ = 4 × ∫ |
(1 + 2 sin ϕ + |
|||||||||
|
||||||||||||||
|
|
2 |
−π |
|
|
|
−π |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
sin 2ϕ |
|
π |
|||
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
2 |
||||||
+ sin |
|
ϕ) dϕ = 4 × ϕ - 2 cosϕ + |
|
- |
|
|
|
|
|
=6π |
||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|
4 |
|
− |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
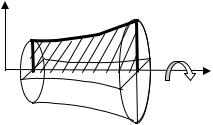
5.2. Объем тела вращения
При вращении криволинейной трапеции вокруг оси
Ох (рис.8) получается тело вращения,
y |
|
|
|
|
||
|
|
y = y(x) |
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
b |
x |
||
|
|
Рис.8. |
|
|
|
|
|
|
|
|
|
|
|
объем которого выражается интегралом |
|
|||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
Vx = π ∫ y2 (x) dx . |
|
(10) |
||
|
|
a |
|
|
|
|
|
|
|
|
|
||
Если криволинейная трапеция |
0 ≤ х ≤ х(у) |
c ≤ y ≤ d враща- |
||||
ется вокруг оси Оу (рис.9), |
|
|
|
|
||
17
y
d
х=x(y) |
|
c |
|
x |
|
Рис.9. |
|
то объем тела вращения выражается интегралом |
|
d |
|
Vy = π ∫ x2 ( y) dy |
(11) |
c |
|
Задача № 3. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями:
y = 2 1 − |
x2 |
, x = −2 , x = 1, y = 0 . |
|
||
9 |
|
|
Решение: Построим фигуру, ограниченную указанными линиями (рис.10).
y = 2 |
1 − |
x2 |
|
- верхняя половина эллипса |
x 2 |
+ |
y 2 |
= 1 , |
|
9 |
|
9 |
4 |
|
|||
где |
a=3, |
b=2 – полуоси эллипса; |
|
|
|
|||
|
х = -2, |
х = 1 – прямые, параллельные оси Оу; |
||||||
|
у = 0 – |
уравнение оси Ох. |
|
|
|
|||
18
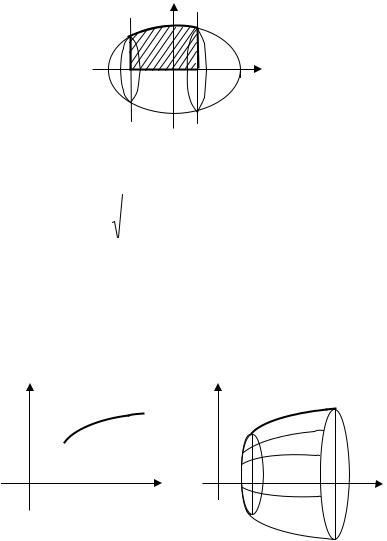
|
у |
|
|
-2 |
0 |
1 |
х |
|
|
|
|
|
х = -2 |
|
х = 1 |
|
Рис.10. |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
x |
2 |
|
|
|||||||||
Vx |
= π |
∫ |
|
2 1 − |
|
|
|
|
dx = 4π |
∫ |
1 |
− |
|
|
|
dx = |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
||||||
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x3 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
8 |
|
|
|
|
32π |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= 4π x − |
|
|
|
|
|
|
= |
|
4π 1 |
− |
|
+ 2 − |
|
|
|
|
|
= |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
− 2 |
|
|
|
|
|
|
27 |
|
|
|
27 |
|
3 |
|||||||
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
5.3. Длина дуги кривой. Площадь поверхности, полученной вращением дуги вокруг осей
у |
|
у |
|
В |
• B |
||
• |
|||
А |
|
A• |
|
• |
|
|
х х
х
Рис.11. Рис.12.
19
