2520
.pdf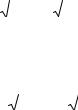
|
|
x = 2 cost |
||||||||
6.25. |
|
y = 2sin t |
||||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= 2 (y £ 2 ) |
|||||||||
|
y |
|||||||||
|
x = 6 cos t |
|||||||||
6.26. |
|
= 4sin t |
||||||||
y |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= 2 3 (y ³ 2 3 ) |
|||||||||
|
y |
|||||||||
|
x = t - sin t |
|||||||||
|
|
=1- cost |
||||||||
6.27. |
y |
|||||||||
|
= 1(y ³1) |
|||||||||
|
y |
|||||||||
|
|
< t < 2π |
||||||||
|
0 |
|||||||||
6.28. |
ρ = 4sin 3ϕ |
|||||||||
6.29. |
ρ = 2 cos 3ϕ |
|||||||||
6.30. |
ρ |
= 2sinϕ |
||||||||
|
= 1 |
|
|
|
|
|
|
|
||
|
ρ |
|
|
|
|
|
|
|
||
40
Задание № 7
Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями:
xy = 4
=
x 1
x = 4
=
y 0
y = 2x − x2
7.02
y = 0
y = sin x
7.03 y = 0
0 ≤ x ≤ π
(y − a)2 = ax
7.04 x = 0y = 2a
y = sin x |
|||
7.05 |
2 |
|
|
y = |
|
x |
|
π |
|||
|
|
||
y = cos x |
|||
|
9 |
|
|
7.06 y = |
|
x2 |
|
|
|
|
|
2π |
2 |
|
|
|
|
|
|
у = ах − х2
( > )
7.07 а 0y = 0
|
|
2 |
= |
3 |
|
|
|
7.08 y |
|
|
x |
||||
|
2 |
||||||
|
2 |
+ y |
2 |
= 1, x > 0 |
|||
x |
|
|
|
|
|||
y = −x2 + 4x
y = 0
y = 2x − x2
y = −x + 2
41
y = 1− x2
7.11 x = 0
x = 
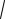y − 2
=x 1
2x − x2 − y = 0
2x2 − 4x + y = 0
7.13x2 + (y − 2)2 = 1
y = ln x
7.14 x = 2
y = 0
7.15(y − 3)2 + 3x = 0x = −3
Вычислить объём тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями:
y = sin x
7.16 x = 0y = 1
y = x3
7.17 y = 0x = 2
x2 − y 2 = 4
7.18
y = ±2
y = sin x |
|||
7.22 |
2 |
|
|
y = |
|
x |
|
π |
|||
|
|
||
|
y 2 = x3 |
|
7.19 |
|
y = 0 |
|
||
|
|
x = 1 |
|
|
|
7.20 |
y 2 = 4 − x |
|
|
|
|
|
x = 0 |
|
y = e x
7.21x = 0
x = 1
=
y 0
7.27y = x28x = y 2
42
y = 
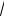x −1y = 0
7.23 |
y = 1 |
||
|
|
1 |
|
|
x = |
|
|
|
2 |
||
|
|
|
|
|
y = arcsin x |
||
7.24 |
|
|
|
y = arccos x |
|||
|
|
|
|
|
y = 0 |
||
|
y = 2x − x2 |
||
7.25 |
|
|
|
y = −x + 2 |
|||
|
x = 0 |
||
|
|
|
|
|
y = x2 − 2x +1 |
||
7.26 |
|
|
|
x = 2 |
|||
y = 0
y = (x −1)2
y = 1
y 2 = x − 2
=
y 0
y = x3
=
y 1
y = arccos x
7.30 y = arcsin x
x = 0
43
|
|
|
Задание № 8 |
Вычислить длину дуги: |
|||
|
y = |
|
|
8.01. |
2 − x2 |
от т. В(-1;1) до т. А(1;1). |
|
8.02. |
2 y = x2 − 2 |
между точками пересечения с осью Ох. |
|
8.03.y = e x , между точками, для которых х = 0 и х =1.
8.04. y = 1 (e x + e− x ) между точками, для которых x = −1 ; 2
х = 0 (цепная линия).
x = 3(t − sin t ) |
|
|
− cost ) |
8.05. y = 3(1 |
|
π≤ t ≤ 2π
x = 4 cos3 t
y = 4 sin 3 t
0 ≤ t ≤ π
4
(циклоида).
(астроида).
|
2 |
(2 − x) |
3 |
|
|
|
16 |
|
|
2 |
|
|
8.07. y = |
2 |
|
− 2; |
|
||||||||
|
|
между точками |
A |
|
|
и |
B 1; |
|
. |
|||
|
|
|
|
|||||||||
|
3 |
|
|
|
|
|
3 |
|
|
3 |
|
|
8.08.y = 4 − x 2 междуточками пересечениякривой с осью Ох.
8.09.Длину дуги кардиоиды ρ = 3(1+ cosϕ ).
8.10.Длину дуги окружности ρ = 2
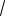3 cosϕ между точка-
ми, для которых ϕ = 0, ϕ = π
4
44
Вычислитьплощадьповерхности, образованнойвращением вокругоси Ох:
8.11.Дуги кривой y 2 = 1 - x , отсеченной прямой x = −3 .
8.12.Дуги кривой y = e− x от х = 0 до х = + ∞.
8.13.Одной полуволны кривой y = sin x вокруг оси Ох.
x = 3(t - sin t ) |
|||
|
- cost ) (циклоида). |
||
8.14. Дуги кривой y = 3(1 |
|||
π £ t £ 2π |
|||
8.15. Дуги кривой y = |
x3 |
|
от х = -2 до х = 2 |
|
|
||
3 |
|
|
|
Вычислить площадь поверхности, образованной вращением вокругоси Оу:
8.16.Дуги кривой x2 = 4 + y , отсеченной прямой у = 2
8.17.Всей кривой x = a ×cos3 t , y = a ×sin 3 t .
8.18.Дуги кривой x2 = 4 y , отсечённой прямой у = 4
8.19.Дуги кривой у = х2 , отсеченной прямой у = 3
4
8.20. Дуги кривой x2 + y 2 = 4 , ограниченной прямыми
у = -1; у = 1
45
Найти координаты центра тяжести плоской фигуры, ограниченной линиями:
|
y = 2x + 4 |
|||||
8.21. |
|
|
|
|
|
|
x = 0 (x ≤ 0) |
||||||
|
|
|
|
|
|
|
|
y = 0 |
|||||
|
y = 4 + x2 |
|||||
|
|
|
|
|
|
|
8.22. |
y = 0 |
|||||
|
|
|
|
|
|
|
|
x = 0 |
|||||
|
|
|
|
|
|
|
|
x = 2 |
|||||
|
|
|
x |
3 |
|
|
|
|
|
|
|
||
|
y = |
|
|
|
||
|
|
|
|
|
||
|
|
3 |
|
|
||
8.23. |
|
y = 0 |
||||
|
|
x = 0 |
||||
|
|
|
|
|
|
|
|
x = 2 |
|||||
|
|
у = |
|
|
||
|
4 + х |
|||||
8.24. |
|
|
|
|
|
|
у = 0 |
|
|
|
|||
|
|
х = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
4 у = 3х2 |
|||||
8.25. |
|
|
|
|
|
|
х = 2 |
||||||
|
|
у = 0 |
||||
|
|
|
|
|
|
|
y = sin 2x
8.26. x = 0
y = 1
y = cos x
y = 0
= π
8.27.x
6
π
|
x = |
|
2 |
|
х2 + 4 у −16 = 0 |
8.28. |
у = 0 |
|
у2 = 5х
8.29. х = 5у = 0 (у > 0)
2x + 3y −12 = 0
=
y 0
x = 1
=
x 4
46
Литература
1. Важдаев, В.П. 64 лекции по математике . Книга 1/ В.П .
Важдаев, М.М . Коган , М.И. Лиогонький , Л.А. Про тасова– Н. Новгород,: ННГАСУ, 2012г.-284с.
2. Данко, П.Е. Высшая математика в упражнениях и за-
дачах. Ч.1/ П.Е. Данко, А.Г. Попов, Т.Я Кожевникова.
—М.: Высшая школа, 1986. — 304 c.
3.Минорский, В.П. Сборник задач по высшей матема тике/В.П. Минорский. - М.: Наука, 2004г. - 336 с.
4.Пискунов, Н.С. Дифференциальное и интегральное исчисление. Т.1/Н.С. Пискунов. — М.: Наука, 1972.
—456 c.
47
Оглавление |
|
1. Понятие определенного интеграла................................... |
0 |
2. Задачи, приводящие к определенному интегралу........... |
5 |
3. Вычисление определенного интеграла............................ |
7 |
3.1.Формула Ньютона-Лейбница.......................................... |
7 |
3.2.Формула интегрирования по частям.............................. |
7 |
3.3.Формула замены переменной ......................................... |
8 |
4. Несобственные интегралы................................................. |
9 |
4.1. Интегралы с бесконечными пределами........................ |
9 |
4.2. Интегралы от неограниченных функций.................... |
10 |
5. Приложения определенного интеграла......................... |
13 |
5.1. Площадь плоской фигуры............................................ |
13 |
5.2. Объем тела вращения ................................................... |
17 |
5.3. Длина дуги кривой. Площадь поверхности, |
|
полученной вращением дуги вокруг осей ......................... |
19 |
5.4. Статические моменты................................................... |
24 |
Задание № 1 ............................................................................. |
27 |
Задание № 2 ............................................................................. |
29 |
Задание № 3 ............................................................................. |
31 |
Задание № 4 ............................................................................. |
33 |
Задание № 5 ............................................................................. |
35 |
Задание № 6 ............................................................................. |
38 |
Задание № 7 ............................................................................. |
41 |
Задание № 8 ............................................................................. |
44 |
Литература.............................................................................. |
47 |
48
Драгунова Валерия Викторовна Опалева Галина Павловна Сенниковская Людмила Семеновна
Определенный интеграл
Учебно-методическое пособие по подготовке к лекционным и практическим занятиям по
дисциплине «Математика» для обучающихся по направлению подготовки 13.03.01_Теплоэнергетика и теплотехника, профиль Промышленная теплоэнергетика
Федеральное государственное бюджетное образовательное учреждение высшего образования «Нижегородский государственный архитектурностроительный университет»
603950, Нижний Новгород, ул. Ильинская, 65. http://www. nngasu.ru, srec@nngasu.ru
49