8

Министерство образования Российской Федерации

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени А.Н. Туполева

Кафедра общей физики

ЛАБОРАТОРНАЯ РАБОТА № 63КК

ИЗУЧЕНИЕ ДИФРАКЦИИ ФРАУНГОФЕРА

ОТ ОДНОЙ ЩЕЛИ

Казань 2002

ИЗУЧЕНИЕ ДИФРАКЦИИ ФРАУНГОФЕРА

ОТ ОДНОЙ ЩЕЛИ

Цель работы: получить дифракционную картину от узкой щели и определить длину волны.

Содержание работы

Дифракцией света называют явления, наблюдаемые при распространении света в среде с неоднородностями, в которых происходит отклонение от законов геометрической оптики: огибание светом препятствий и проникновение его в область геометрической тени. Дифракция Фраунгофера наблюдается в параллельных лучах, получаемых с помощью линз. Если использовать лазер, то можно обойтись без линз, так как излучаемые им световые пучки являются параллельными.

Пусть параллельный пучок монохроматического света с длиной волны  падает нормально на преграду с бесконечно длинной щелью шириной АВ = в (рис. 1)

Согласно принципу Гюйгенса, каждая точка плоскости щели, до которой дошел фронт волны, является источником вторичных волн распространяющихся во все стороны. Таким образом, за преградой световые волны проникают в область геометрической тени. Дифрагированные пучки являются когерентными и могут интерферировать при наложении на экране. Если экран находится на большом расстоянии l от щели ( l = в² /  ), то лучи, идущие в точку Р от краев щели, будут практически параллельными, то есть будет соблюдаться условие дифракции Фраунгофера. Так, как лучи АР и ВР почти параллельны, то их разность хода КВ =  равна  = в sin  .

Для расчета дифракционной картины, получаемой на экране, воспользуемся методом зон Френеля. Пусть в некотором направлении разность хода  от краев щели равна  к  , где к = 1, 2, 3, ... Тогда щель АВ можно разбить на 2 к равных по ширине зон , причем разность хода соседних зон равна /2 (рис. 2).

Все зоны в заданном направлении излучают свет совершенно одинаково. При интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как эти зоны вызывают колебания с одинаковыми амплитудами, но противоположными фазами. В другом направлении разность хода может быть равна  = (2 к + 1) и число зон, на которые разобьется щель АВ, будет нечетным. Действие одной из зон окажется некомпенсированным и в этом направлении будет наблюдаться максимум интенсивности. Поэтому результат интерференции света в точке определяется тем, сколько зон Френеля укладывается в щели.

Если число зон четное, то наблюдается дифракционный минимум (полная темнота). Следовательно, условием минимума является

(1)

Если число зон нечетное, наблюдается дифракционный максимум. Следовательно, условием максимума является

(2)

В зависимости от величины угла  в щели может укладываться четное или нечетное число зон Френеля. Поэтому на экране наблюдается периодическое распределение интенсивности излучения с максимумами и минимумами (рис. 3). Величина к называется порядком дифракционного максимума.

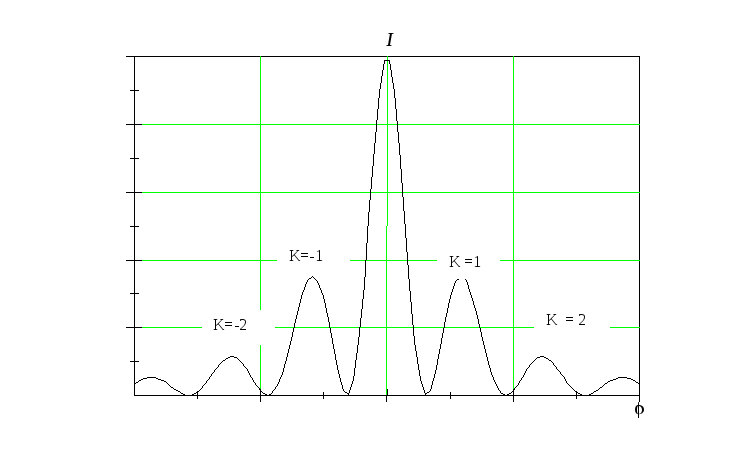
Рис.3

В направлении  = 0 наблюдается самый интенсивный центральный максимум нулевого порядка: здесь колебания, вызываемые всеми участками щели, совершаются в одной фазе. При постепенном увеличении угла  по обе стороны от центральной полосы будут наблюдаться чередующиеся темные и светлые полосы. В направлениях, определяемых условием (2), будут располагаться светлые полосы: при к = 1 - максимумы первого порядка, при к = 2 - максимумы второго порядка, и т.д.

Рассмотренный выше расчет дифракционной картины методом зон Френеля является приближенным. Точное решение этой задачи осуществляется путем разбиения щели на бесконечное число одинаковых узких полос. Приведем без вывода формулы для амплитуды А_ и интенсивности света I_ в различных точках экрана

, (3)

, (4)

где  =(b/) sin, А₀ и I₀ - амплитуда и интенсивность света в середине дифракционной картины (при  = 0) , и I_ - амплитуда и интенсивность света в точке, положение которой определяется углом  .

Из формулы (4) и рис. 3 видно, что центральный максимум значительно превосходит по интенсивности остальные максимумы:

I₀ : I₁ : I₂ = 1 : 0,045 : 0,016. Наблюдаемость дифракционной картины Фраунгофера зависит от ширины щели, а также от расстояния l от щели до экрана. Если невелико, то есть щель очень узка, то наблюдающиеся максимумы очень широки и дифракционная картина мало контрастна. Наоборот, если велико (широкая щель), то центральный максимум очень узкий и яркий. Выведем формулу для определения длины волны с использованием условия (1). На рис.4 линия О₁О проходит через центр щели перпендикулярно линии АВ. Угол ВАК равен углу . Поэтому треугольники АВК и ОРО₁ подобны. Из подобия следует

или

(5).

Из (1) и (5) следует

С учетом того, что y m значительно меньше l, можем принять О₁Рl. Тогда получим

и

(6).

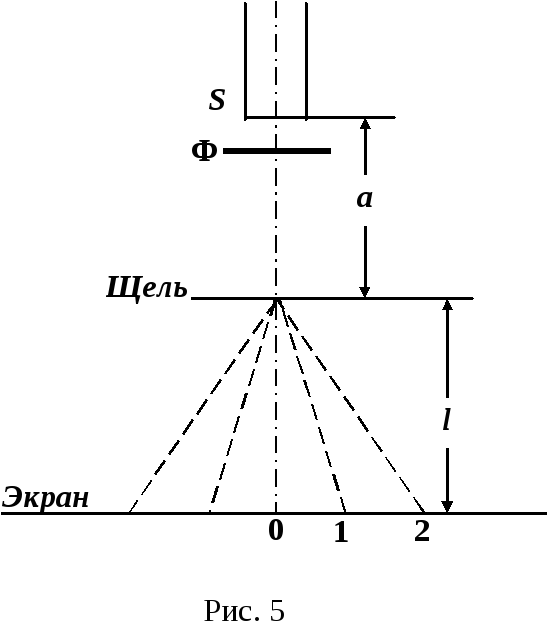
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

Установка собирается по схеме рис. 4 Приборы и принадлежности: источник плоских волн белого света S, щель регулируемая, экран светофильтр Ф. Расстояние от щели до экрана l= 1,15 м. Цифры 1 и 2 условно показывают положения максимумов первого и второго порядков.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Начертить в тетради таблицу 1.

Таблица 1

№ экс.	k	j	yз	y1	b	1	цвет	
1	3	1
2	3	1
3	3	1
4	3	1
5	3	1
6	3	1
7	3	1
8	3	1

2. Включить компьютер.

3. Запустить программу 63К.ЕХЕ. Для этого указать курсором на 63К и щелкнуть левой кнопкой мышки (в дальнейшем эту команду обозначим L ' на 63К). Изучить информацию на экране. В левой части экрана расположены шкала окуляра, дифракционные полосы, ползунок для перемещения дифракционных полос, ползунок для установки ширины щели, справа- панель управления. Совместить центр дифракционных полос с точкой 0 шкалы окуляра путем перемещения дифракционных полос с помощью ползунка. ОК.

4. Установить ширину щели путем перемещения ползунка и записать ее значение в таб.1. В данных опытах она может находиться в пределах от 0,00001 до 0,00004 м.

Опыт 1

5. L' на Опыт 1. ОК.

6. Записать значения у₁, у_з и цвет дифракционной картины в таб.1.

Опыт 2

7. L' на Опыт 2. ОК.

8. Повторить пункт 6.

Опыт 3

9. L' на Опыт 3. ОК.

10.Повторить пункт 6.

Опыт 4

10. L' на Опыт 4. ОК.

11. Повторить пункт 6.

Опыт 5

12. L' на Опыт 5. ОК.

13. Повторить пункт 6.

Опыт 6

14. L' на Опыт 6. ОК.

15. Повторить пункт 6.

Опыт 7

1б. L' на Опыт 7.ОК.

17. Повторить пункт 6.

Опыт 8

18. L' на Опыт 8. ОК.

18. Повторить пункт 6.

19. L' на Калькулятор. По формуле (6) рассчитать длину волны и записать в таб.1.

20. Таблицу 1 переписать в тетрадь.

Контрольные вопросы

1. Что называется дифракцией света?

2. При каких условиях наблюдается дифракция Фраунгофера?

3. Вывести условие максимума и минимума света при дифракции от одной щели.

4. Как влияет ширина щели на дифракционную картину?

Литература

1. Савельев И.В. Курс общей физики. Т.З.М., Наука, 1971.

2. Яворский Б.М., Детлаф А.А. Курс физики. Т.3. М. Высшая школа, 1972.

3. Поль Р.В. Оптика и атомная физика, М., Наука, 1966.

4. Лабораторный практикум по физике. Под ред. А. С. Ахматова, М., Высшая школа. 1980.