Зарядка конденсатора.

При полной разрядке конденсатора (при нулевом показании вольтметра, измеряющего напряжение на конденсаторе) мгновенно переключим переключатель Пв положение 1 (см. рис. 1).

По второму закону Кирхгофа можно записать:

U_R+U_C=. (7)

Из (7) получим:

.

Преобразуем это уравнение к следующему виду:

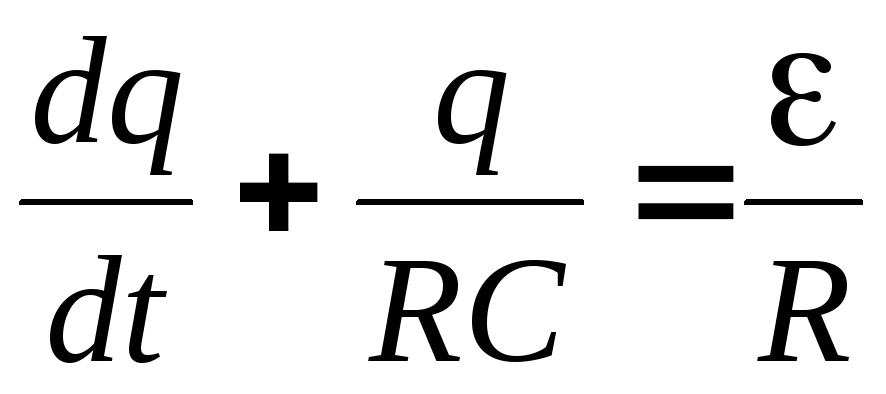. (8)

Уравнение (8) представляет собой линейное неоднородное дифференциальное уравнение 1-го порядка. Как известно из теории дифференциальных уравнений, общее решение линейного неоднородного дифференциального уравнения можно получить, прибавив любое его частное решение к общему решению соответствующего однородного уравнения.

Уравнение (5) дает общее решение однородного уравнения. Частное решение получим из условия, что конденсатор заряжается до напряжения U_C =  при бесконечно большом времени зарядки. Поэтому

q_частн= ·С.(9)

Сложив (5) и (9), получим

. (10)

Найдем const из начального условия приt= 0, U_C=0, q=0.

, const =   C.

С учетом этого из (10) находим

.

Разделив это уравнение на С, с учетом (2), запишем:

. (11)

Время релаксации.

Из уравнений (6) и (11) следует, что напряжение на емкости изменяется по экспоненциальному закону. Напряжение уменьшается или возрастает тем медленнее, чем больше произведение RC. Поэтому произведение RCназываютпостоянной времении обозначают буквой(тау).

 = RC.(12)

Выясним физический смысл постоянной времени . В соответствии с (6) можем записать

.

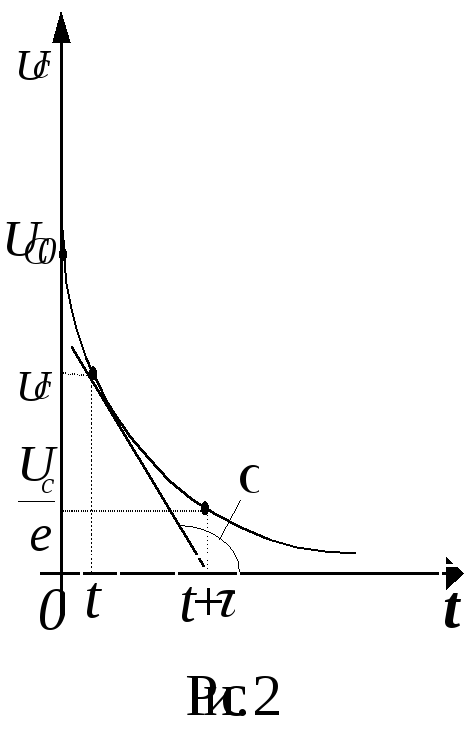
Следовательно, - это время, за которое напряжение на конденсаторе уменьшится ве раз.

Постоянную времени называют также временем релаксации.

Найдем уравнение касательной графика функции (6) с учетом (12).

.

Из рис. 2 следует, что - это время, за которое напряжение на конденсаторе достигло бы установившегося значенияU_C=0, если с моментаtскорость изменения напряжения на конденсаторе не изменялась бы.

Описание лабораторной установки

Принципиальная электрическая схема лабораторной установки представлена на рис. 1. Все элементы схемы собраны в одной установке. В установке также имеется вольтметр, измеряющий напряжение на конденсаторе (на рис. 1 не показан). Используется высокоомный вольтметр, поэтому через него проходит очень небольшой ток и вольтметр практически не влияет на результаты эксперимента.

Методика проведения эксперимента

1. Начертить в тетради таблицу 1.

Таблица 1

напряжения Uс, В	Время изменения напряжения t, с			Среднее время tср , с
	1-й опыт	2-й опыт	3-й опыт
Зарядка конденсатора
0,1
0,2
0,3
0,4
0,5
0,6
Разрядка конденсатора
0,6
0,5
0,4
0,3
0,2
0,1

2. Включить компьютер.

3. Запустить программу 26К.ЕХЕ. Для этого указать курсором на 26К.ЕХЕ и щелкнуть левой кнопкой мышки (в дальнейшем эту команду обозначим L’ на 26К.ЕХЕ). Изучить информацию на экране.

Предварительный опыт –наблюдение процессов зарядки и разрядки

4. Установить значение сопротивления Rпутем перемещения ползунка, расположенного надR. Для этогоL’ на ползунке и при нажатой левой кнопке мышкой перемещать курсор в нужном направлении.

5. Установить значение С. Для этого удалить ненужное значениеСс помощью командыDeleteи записать желаемое значениеС. Диапазон измененияСот 222 до 999 мкФ .

6. L’на командеПуски наблюдать процесс зарядки до значения напряжения 0,8 В иL’на командеПауза.

7. L’на командеЗавершить.

8. L’на командеПуски наблюдать процесс разрядки. ПриU_с= 0,1 В L’на командеПауза.

9. L’на командеЗавершить.