
книги / Сопротивление материалов.-1
.pdf
Сечение |
Значение изгибающего момента |
|
Участок В |
|
МΣ = –300 – 19,84 = –319,84 Н м |
Участок ВЕ |
Е |
МΣ = –319,84 Н м |
Участок ЕD |
Е |
МΣ = 300 – 19,84 = 280,16 Н м |
Участок ЕD |
D |
МΣ = 280,16 Н м |
Участок DK |
D |
МΣ = –100 – 19,84 = –119,84 Н м |
Участок DK |
K |
МΣ = –119,84 Н м |
Участок KС |
K |
МΣ = –19,84 Н м |
Участок KС |
С |
МΣ = –19,84 Н м |
2. Деформационная проверка решения.
Умножая суммарную эпюру крутящих моментов (МΣ) на эпюру M1 по правилу Верещагина, определяем угол закручива-
ния сечения С относительно В, который по условию закрепления должен быть равен нулю.
ϕ |
= Σ |
li |
(M |
Σc |
M |
1i |
) = |
319,84 0,5l1 1 |
− |
280,16 0,5l1 1 |
− |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
C −B |
|
|
GJi |
|
|
|
|
|
|
GJP1 |
|
|
|
|
|
|
|
|
GJP1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
− |
280,16 l2 1 |
+ |
119,84 0,5l3 1 |
+ |
19,84 0,5l3 1 |
= |
|
|
||||||||||||||||||||
|
|
|
|
GJP2 |
|
|
|
|
|
GJP3 |
|
|
|
|
GJP3 |
|
|
|
|
|
|||||||||
= |
l |
2 |
|
|
|
|
−280,16 − |
280,16 |
|
+ |
119,84 |
+ |
19,84 |
= |
|
||||||||||||||
|
|
319,84 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
GJP1 |
|
|
|
|
|
|
|
|
2,07 |
|
|
|
1, 46 |
|
|
1, 46 |
|
|
||||||||||
|
|
|
= |
|
l2 |
|
(414,9 −415,19) = |
|
|
0, 29l2 |
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
GJP1 |
|
|
|
|
|
|
|
|
|
GJP1 |
|
|
|
|
|
|
|
||||||
Погрешность составляет 0,07 %.
3. Расчет размеров поперечного сечения вала.
Принять [τ] = 80 МПа. Опасные сечения будут на участке ВЕ, так как здесь наблюдается наибольший крутящий момент при наименьшем диаметре вала.
Из условия прочности
τmax = | MΣ |max ≤[τ],
Wρ1
171
|
|
πd3 |
|
|
|
где W |
= |
1 |
, |
|
|
|
|
|
|||
ρ1 |
|
16 |
|
|
|
|
|
|
|
|
|
определяем диаметр |
|
|
|||
|
|
|
d1 ≥ 3 |
319,84 16 |
= 2,73 см. |
|
|
|
|
3,14 80 |
|
Принимаем диаметр d1 = 28 мм, d2 = 32 мм, d3 = 30 мм. 4. Определение угла закручивания сечения А.
Для определения угла закручивания сечения А приложим в основном состоянии единичный скручивающий момент Mк1 =1
в этомсечении ипостроим эпюру Mк (см. рис. 8.33, ж).
Перемножая эпюру МΣ и эпюру Mк по правилу Верещагина, определим угол закручивания сечения А.
ϕ |
A |
= 319,84 0,5l1 1 − 280,16 0,5l1 1 =15,872 = |
||||||||||||
|
|
|
|
GJρ1 |
|
|
GJρ1 |
|
|
GJρ1 |
|
|||
|
|
|
|
|
|
|
|
|||||||
|
|
= |
|
|
|
15,872 32 |
|
|
=3,3 |
10−3 |
рад; |
|||
|
|
|
|
10 |
4 |
10 |
−8 |
|||||||
|
|
8 |
10 |
3,14 2,8 |
|
|
|
|
|
|
||||
или
ϕA =3,3 10−3 180o = 0,19o . 3,14
Расчет статически неопределимых систем при растяжении-сжатии
Пример
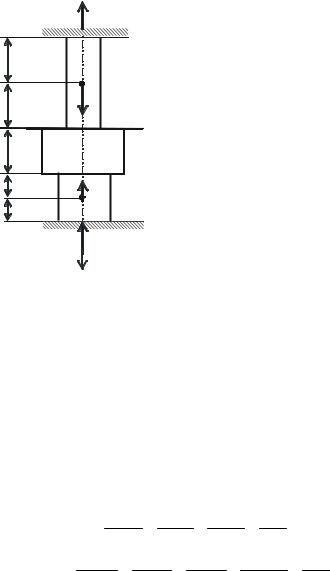
Для стержня, показанного на рис. 8.34, определить:
а) диаметр на различных участках из условия прочности; б) перемещение сечения 1-1 стержня.
172
RВ |
Материал стержня – сталь (чу- |
Вгун). Модуль продольной упругости:
|
|
|
|
|
для стали Е = 2 105 МПа, для чугуна |
|||
l |
|
А1 |
K |
|
Е = 1,2 105 МПа). Предел текучести |
|||
|
|
|
для стали 30, σТ = 300 МПа, предел |
|||||
l |
|
|
|
|
прочности |
для |
чугуна |
СЧ28-48 |
1 |
F1 |
C |
|
1 σпч+ =280 МПа, σпч– |
= 1000 МПа. |
|||
l |
А2 |
|
|
|
l = 0,5 м; А1 = А; А2 = 3А; |
|||
|
|
|
А3 = 2А; F1 = 120 кН; F2 = 80 кН. |
|||||
|
|
|
|
|
||||
1 |
А3 |
F2 |
|
D |
1. Раскрыть статическую неоп- |
|||
2 l |
L |
|||||||
1 l |
|
|
|
ределимость |
системы с помощью |
|||
2 |
|
|
|
|
канонических уравнений |
метода |
||
|
|
A |
RA |
|
сил. |
|
|
|
|
|
|
Задача один раз статически не- |
|||||
|
|
|
z |
|
||||
|
|
|
|
определима, т.к. уравнение статики |
||||
Рис. 8.34. |
может быть записано одно ΣFZ = 0, |
|
а неизвестных реакций две (RA, RB), |
||
|
рис. 8.34.
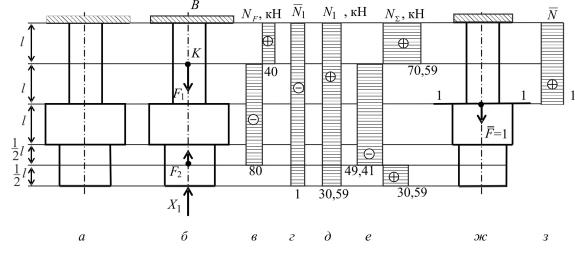
Основная система может быть выбрана путем отбрасывания связи А или В (рис. 8.35, а).
Загружая основную систему силами F1, F2 и неизвестной силой Х1, получаем эквивалентную систему (см. рис. 8.35, б).
Неизвестная сила Х1 определяется из канонического уравнения:
δ11Х1 + ∆1F = 0.
Коэффициент δ11 и свободный член уравнения ∆1F определяем по способу Верещагина.
δ11 =1E2lА1 + E1 l31А + E1 l21А = 617EАl ;
∆1F = − 40EАl 1 + 80EАl 1 + 803ElА1 + 802E0,5А l = 5206EАl ; X1 = −30,59 кН.
173
174
Рис. 8.35.
174
Строим эпюру N 1 = N1 X1 (см. рис. 8.35, д).
2. Построить суммарную эпюру продольных сил. На основании принципа независимости действия сил NΣi = NFi + NX1i .
Сечение |
Значение изгибающего момента |
А |
NΣ = 30,59 кН |
L (участок AL) |
NΣ = 30,59 кН |
L, K (участки LD, DC, CK) |
NΣ = –80 + 30,59 = –49,41 кН |
K (участок KВ) |
NΣ = 40 + 30,59 = 70,59 кН |
Эпюра продольных сил (NΣ) приведена на рис. 8.35, е.
3. Деформационная проверка решения.
Перемножая по правилу Верещагина эпюру NΣ и эпюру N1, определяем перемещение сечения А, которое по условию наложенной связи должно быть равно нулю.
n |
|
|
|
|
30,59 0,5l |
|
49, 41 0,5l |
|
49, 41l |
|
49, 41l |
|
|
ω M |
|
|
|
|
|
|
|||||||
∆A = ∑ |
i |
i |
= − |
|
+ |
|
+ |
|
+ |
|
− |
||
E |
А |
2EА |
2EА |
3EА |
EА |
||||||||
i=1 |
|
|
i |
|
|
|
|
|
|
|
|
||
−70,59EА l = ElА(−7,65 +12,35 +16, 47 + 49, 41−70,59) =
=ElА(−78, 24 + 78, 23) ≈ 0,E01А .
Погрешность составляет: ε = 78,0,0123 100 % ≈ 0,013 % .
4. Рассчитать размеры поперечного сечения стержня
σmax = NmaxА ≤[σ].
Наиболее опасными сечениями являются сечения на участке ВK. На этом участке наибольшая продольная сила N = 70,59 кН при наименьшем сечении стержня. Принимая коэффициент запаса n = 1,5, определяем допускаемое напряжение
[σ]= σnT = 3001,5 = 200 МПа в случае стального стержня (сталь 30).
Определяем диаметр d1 на 1-м участке.
175
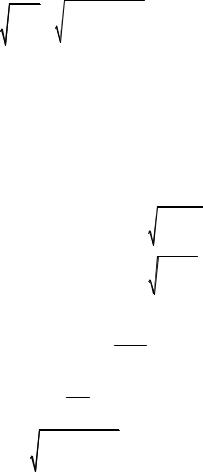
d ≥ |
4N |
= |
4 70,59 103 |
= 21,2 мм. |
|
π[σ] |
3,14 200 |
||||
1 |
|
|
Принимаемпонормальномурядулинейныхразмеровd1 = 22 мм.
|
πd |
2 |
|
3,14 222 |
= 380 мм2 . |
А = |
1 |
= |
|
||
|
|
||||
1 |
4 |
|
|
4 |
|
|
|
|
|
||
Напряжение в этом случае будет равно
σmax = |
70,59 103 4 |
=186 |
МПа. |
||||||
3,14 222 |
|||||||||
|
|
|
|
|
|
|
|||
А = 3A = 380 3 =1140 |
мм2 ; |
d |
2 |
≥ |
4 1140 |
= 38,1 мм; |
|||
|
|
||||||||
2 |
|
|
|
|
3,14 |
|
|
||
|
|
|
|
|
|
|
|
||
А = 2 A = 380 2 = 760 |
мм2 ; |
d |
3 |
≥ |
4 760 |
= 31,1 мм. |
|||
|
|||||||||
3 |
|
|
|
|
3,14 |
|
|
||
|
|
|
|
|
|
|
|
||
σ+
Для чугунного стержня [σ]+ = [пчn] ; n = 2,5;
[σ]+ = 2802,5 =112 МПа.
|
|
d |
≥ |
|
4 70,59 103 |
= 28,3 мм. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
3,14 112 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
πd 2 |
|
|
|
|
3,14 282 |
|
|
Принимаем d1 |
= |
28 мм. Площадь |
А = |
1 |
|
= |
|
|
= |
||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= 615, 4 мм2 . Напряжение в этом случае |
на |
|
|
участке ВK |
|||||||||||
σmax+ = |
70,59 103 |
=114,7 МПа. Перенапряжение ε |
= |
114,7 −112 |
× |
||||||||||
|
|
|
112 |
|
|||||||||||
615, 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
×100 % = 2, 4 % , что допустимо.
176
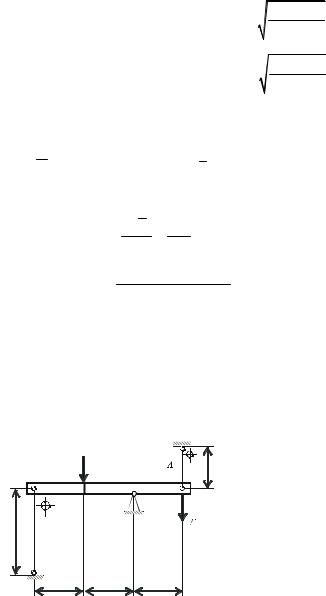
А = 3A = 615,4 3 =1846,2 |
мм2 ; |
d |
2 |
= |
4 1846,2 |
= 48,5 мм. |
||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3,14 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
А = 2 A = 615,4 2 =1230,8 |
мм2 ; |
d |
3 |
= |
4 1230,8 |
= 39,6 мм. |
||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,14 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. Определить перемещения сечения 1-1 стального стержня. |
||||||||||||||||||||
Для определения перемещения 1-1 в стержне АВ необходимо |
||||||||||||||||||||
в основной системе (см. рис. 8.35, ж) приложить единичную |
||||||||||||||||||||
силу F = 1, построить эпюру N (см. рис. 8.35, з) и затем пере- |
||||||||||||||||||||
множить эту эпюру и эпюру NΣ по правилу Верещагина. |
||||||||||||||||||||
|
|
n |
|
ω N |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆l1−1 = ∑ EFi |
i |
= |
EF (70,59 l 1−49,41 l 1) = |
. |
|
|||||||||||||
|
|
i=1 |
i |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
= |
0,5 21,18 103 103 |
= 0,14 |
мм. |
|
|
|
|
|||||||||||
|
|
|
|
11 |
|
380 10 |
−6 |
|
|
|
|
|||||||||
|
|
|
|
2 10 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Сечение 1-1 перемещается вниз на 0,14 мм. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
Пример |
|
|
|
|
|
|
|
|
|
||
Абсолютно жесткий брус А-В шарнирно поддерживается |
||||||||||||||||||||
стальными стержнями, крепится посредством опорных уст- |
||||||||||||||||||||
ройств (рис. 8.36) и нагружен силами F1 и F2. Произвести проек- |
||||||||||||||||||||
тировочный расчет, принимая коэффициент запаса n = 2, предел |
||||||||||||||||||||
|
|
|
|
|
|
|
K |
|
|
|
текучести |
σт |
= |
380 МПа, |
||||||
|
|
F1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
l |
|
F1 |
= 2F2, F2 |
= |
|
200 кН, |
||||||
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
А |
|
|
|
|
|
|
|
|
B |
|
A1 = 2A, A2 = A. Брус АВ |
|||||||||
|
|
|
C |
|
|
|
|
|
|
|
принять недеформируемым. |
|||||||||
|
|
|
|
|
|
|
|
|
|
Устойчивость |
|
стержней |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2l 2l |
A1 |
|
|
|
|
|
|
|
2 |
|
обеспечена. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Определить |
степень |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
статической |
неопределимо- |
||||||||
D |
l |
l |
|
|
|
l |
|
|
|
|
сти. |
Неизвестных усилий 4 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Рис. 8.36. |
|
|
|
|
|
|
(два на опоре С и по одно- |
|||||||||||
|
|
|
|
|
|
|
|
му в 1-м и 2-м стержнях). |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
177 |
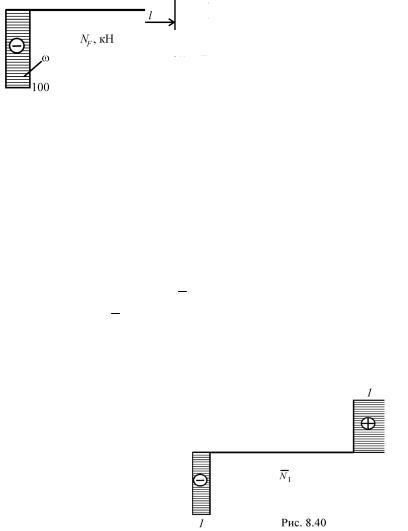
Уравнений статики, свойственных для данной системы, можно записать 3. Следовательно, задача один раз статически неопределима.
2. Раскрыть статическую неопределимость системы.
Рис. 8.37. |
Рис. 8.38. |
Выбирается основная система путем отбрасывания связи K или D (рис. 8.37). Основная система превращается в эквивалентную систему (рис. 8.38). Коэффициенты канонического уравнения δ11Х1 + ∆1F = 0 определяются способом Верещагина. На рис. 8.39, 8.40 приведены эпюры продольных сил в основном
состоянии от сил F1, F2 и X1 =1. Усилия в стержнях от заданных сил F1, F2 и X1 =1 определяются из уравнения статики
ΣМС = 0; N |
2l + F l − F l = 0 ; |
N |
= −F1 + F2 |
= −100 |
кН. |
|
1 |
1 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
Стержень 1 – сжимается.
Рис. 8.39. |
Рис. 8.40. |
|
|
178
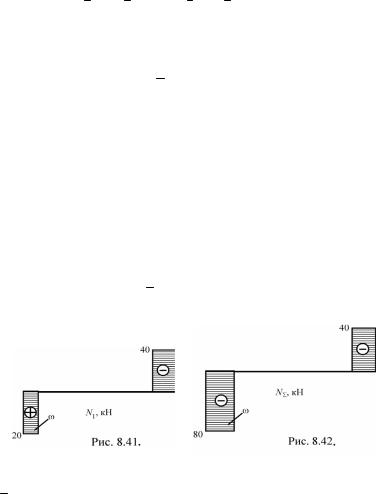
X1 l +N1 2l =0; X1 =1; N1 = − 0,5.
От единичной силы |
|
|
1 =1 первый стержень также сжи- |
|||||||||||
X |
||||||||||||||
мается. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n ω N |
|
|
|
|
0,5 2l 0,5 |
|
||||||
δ11 = ∑ |
EAi Ci |
= |
|
EA |
+ |
|||||||||
|
|
i=1 |
|
|
|
|
i |
|
|
1 |
|
|||
|
|
+ |
1 l 1 |
= |
1, 25l |
. |
|
|||||||
|
|
|
EA |
|
|
EA |
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
n |
|
|
|
|
|
100 2l 0,5 |
|
|||||
|
|
ω N |
|
|
||||||||||
∆1F = ∑ |
|
EAi Ci = |
|
2EA |
= |
|||||||||
|
|
i=1 |
|
|
|
|
i |
|
|
|
|
|
||
= |
50l |
, X1 = − |
|
50 |
|
= −40 кН. |
|
|||||||
EA |
|
|
|
|
||||||||||
|
|
1,25 |
|
|
|
|||||||||
Учитывая, что N1 = = N1 X1 и NΣi = NFi +N1 , строим эпюры
N1 (рис. 8.41) и NΣ (рис. 8.42).
3. Деформационная проверка.
Перемножая по правилу Верещагина эпюру NΣ и эпюру N1 , определяем перемещение связи K, которое по условию равно нулю.
n |
ω |
|
|
|
80 2l 0,5 |
|
40 l 1 |
|
N |
|
|
||||||
∆K =∑ |
i i |
= |
2EA |
− |
EA |
=0. |
||
EA |
||||||||
i=1 |
|
i |
|
|
|
|
||
179
4.Определить диаметры стержней из условия прочности
σ= NA =[σ]. Напряжение в первом и втором равны по величине
σI = |
|
80 |
|
|
|
|
σII = |
|
40 |
|
. Допускаемое |
напряжение |
[σ]= |
σT |
= |
|||||||||||||
|
|
; |
|
|
|
|
||||||||||||||||||||||
|
2 A |
|
A |
|
n |
|||||||||||||||||||||||
= |
|
380 |
|
=190 |
|
|
МПа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A ≥ |
40 103 |
|
= 210,5 мм2 ; |
d2 = |
A2 4 |
= |
210,5 4 =16,4 |
мм. |
||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
190 |
|
|
|
|
|
|
|
3,14 |
|
3,14 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
πd 2 |
|
|
|
|
|
|
Принимаем |
диаметр |
d2 = 17 |
мм. |
Тогда |
A |
= |
|
|
2 |
|
= |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
3,14 172 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|
|
2 |
d = |
|
A1 4 |
= |
|||||||||||||
= |
|
|
|
|
|
|
=226,9 мм , |
|
A =2A =2 226,9 =453,8 мм , |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
1 |
|
|
3,14 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
|
453,8 4 |
|
= 24,04 |
мм. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3,14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Вопросы для самопроверки
1.Что называется статически неопределимыми системами?
2.Как определяется степень статической неопределимости?
3.Что понимается под заданной, основной и эквивалентной системами?
4.Какой физический смысл заложен в канонических уравнениях метода сил?
5.Какие упругие стержневые системы называются симметричными и кососимметричными с точки зрения нагружения?
6.Что дает использование свойств симметрии при раскрытии статической неопределимости?
7.Для чего проводится деформационная проверка при раскрытии статической неопределимости?
Для лучшего усвоения материала рекомендуется изучить источники [1] (гл. 6, § 6.1–6.6); [2] (гл. 7, § 22–24).
180
