книги / Физика для бакалавра. Ч. 2-1

Применение интерферометров очень многообразно. Кроме перечисленного, они применяются для изучения качества изготовления оптических деталей, измерения углов, исследования быстропротекающих процессов, происходящих в воздухе, обтекающем летательные аппараты, и т.д. Применяя интерферометр, Майкельсон впервые провел сравнение международного эталона метра с длиной стандарта световой волны. С помощью интерферометров исследовалось также распространение света в движущихся телах, что привело к фундаментальным изменениям представлений о пространстве и времени.

23.7. Многолучевая интерференция

При наложении двух когерентных световых пучков образуются интерференционные полосы, в которых распределение

интенсивности описывается функцией I cos2 k 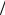2, где –

разность хода пучков. Максимумы и минимумы интенсивности, т.е. светлые и темные полосы, в двухлучевой интерференционной картине имеют одинаковую ширину. При наложении большого числа пучков распределение интенсивности в интерференционной картине существенно иное. Изменение характера интерференционных полос при увеличении числа n пучков качественно можно предсказать на основе закона сохранения энергии. Амплитуда световых колебаний в максимумах интенсивности, где сложение колебаний происходит в одинаковой фазе, в n раз больше, а интенсивность в n2 раз больше, чем от одного пучка (при условии, что когерентные пучки имеют одинаковую или почти одинаковую интенсивность). Но полная энергия, приходящаяся на одну интерференционную полосу, лишь в n раз больше, чем в одном пучке. Увеличение интенсивности в максимумах в n2 раз возможно только в случае существенного перераспределения потока энергии в пространстве: при прежнем расстоянии между светлыми полосами их ширина должна быть примерно в n раз меньше этого расстояния. Благо-

141

даря образованию узких максимумов, т.е. резких светлых полос, разделенных широкими темными промежутками, многолучевая интерференция получила важное практическое применение. Большое число когерентных световых пучков может возникнуть в результате дифракции при прохождении плоской волны через экран с одинаковыми регулярно расположенными отверстиями (метод деления волнового фронта). Распределение интенсивности в такой многолучевой интерференционной картине будет рассмотрено на примере дифракционной решетки. Здесь мы изучим интерференцию при многократных отражениях света от двух параллельных поверхностей (метод деления амплитуды).

В заключение главы приведем основные законы и соотношения величин интерференции света:

Вопросы для самоконтроля

1.Каковы основные положения и выводы корпускулярной

иволновой теорий света? Почему возникло представление

одвойственной корпускулярно-волновой природе света?

2.Каковы условия возникновения интерференции?

3.Какую величину называют временем когерентности? длиной когерентности? Какова связь между ними?

4.Для чего вводятся понятия временной и пространственной когерентностей?

5.Что такое оптическая длина пути? оптическая разность

хода?

143

6.Каковы условия возникновения интерференционного максимума и минимума?

7.Почему интерференцию можно наблюдать от двух лазеров и нельзя от двух электродов?

8.Каковы условия максимума и минимума интерференции

втонких пленках?

9.Что такое полосы равной толщины и равного наклона? Где они локализованы?

10.Почему центр колец Ньютона, наблюдаемых в проходящем свете, обычно светлый?

11.Что называется интерферометром и для каких целей они

служат?

12.Каковы особенности многолучевой интерференции?

Проверочные тесты

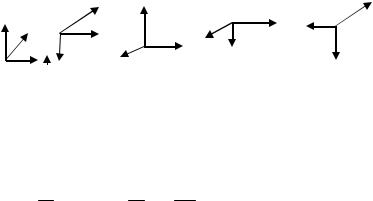
1. Явление интерференции света говорит о его волновой природе. В световой волне, являющейся электромагнитной, век-

торы E,H,v взаимно перпендикулярны и расположены определенным образом. На каком из рисунков (1–5) правильно изображено взаимное расположение векторов E,H,v ?

2. Сколько длин волн монохроматического света с частотой ν уложитсянапутиl,взятомвсредеcпоказателемпреломленияn?

1) cnl ; 2) сl n ; 3) lcn ; 4) l cn ; 5) l cn .

144

3. Два когерентных луча приходят в некоторую точку экрана с разностью фаз колебаний вектора E, равной δ. Выберите те δ, при значении которых в этой точке экрана будет темнота.

1) δ = 2; 2) δ = π; 3) δ = 32 π; 4) δ = 2π; 5) δ = 3π.

4.Два точечных когерентных источника света находятся

вспирте (n = 1,4) на расстоянии 6,4 см друг от друга. Определите оптическую разность хода лучей, пришедших в точку, лежащую на расстоянии 20 см от одного источника, отсчитанном по перпендикуляру к прямой, соединяющей источники.

1) 0,72 см; 2) 1,0 см; 3) 1,4 см; 4) 2,8 см; 5) 3,2 см.

5.На рисунке изображена схема для наблюдения колец Ньютона. Выберите из нижеприведенных те изменения условий наблюдения, при которых диаметры колец увеличиваются. Плосковыпуклая линза большого радиуса прижимается выпуклой стороной к плоской стеклянной пластинке так, что между ними образуется воздушный клин.

rk

1)линзу берут с меньшим радиусом кривизны;

2)линзу берут с большим радиусом кривизны;

3)длину волны света увеличивают;

4)клин между линзой и пластинкой заполнен жидкостью.

6. Выберите из нижеприведенных выражений разности фаз колебаний вектора E в двух лучах, пришедших в некоторую

145

точку экрана, то, которое представляет собой условие максимума света в этой точке.

1)δ = k π; 2) δ = (k + 1) π; 3) δ = (2k + 1) π; 4) δ = 2k π; 5) δ =

=(2k + 1) 2.

Здесь k = 0, 1, 2, 3 …

7. Оптическая разность хода двух лучей, пришедших в некоторую точку экрана от двух когерентных источников, составляет 1,5λ. Чему равна соответствующая разность фаз коле-

баний вектора E в этой точке? 1) π/3; 2) π/2; 3) π; 4) 2π; 5) 3π.

8.На пути световой волны, идущей в воздухе, поставили стеклянную пластинку (n = 1,55) толщиной h = 2,0 мм. На сколько изменится оптическая длина пути луча, если волна падает на пластинку нормально?

1) на 3,1 мм; 2) на 0,050 мм; 3) на 1,1 мм; 4) на 3,5 мм; 5) на 0,55 мм.

9.Определите расстояние между мнимыми источниками

вопыте с зеркалами Френеля, если расстояние между темными полосами на экране равно 3,0 мм, а расстояние от мнимых источников до экрана – 2,0 м. Длина световой волны монохроматического света 0,600 мкм.

1) 0,10 мм; 2) 0,20 мм; 3) 0,30 мм; 4) 0,40 мм; 5) 0,50 мм.

10.На рисунке изображена установка для наблюдения колец Ньютона. Плосковыпуклая линза большого радиуса прижимается выпуклой стороной к плоской стеклянной пластинке так, что между ними образуется воздушный клин. Выберите из нижеприведенных те изменения условий наблюдения, при которых диаметры колец Ньютона уменьшаются.

146

rk

1)пространство между линзой и пластинкой заполняют жидкостью;

2)линзу заменяет надругую, сменьшим радиусомкривизны;

3)линзу заменяютна другую, сбольшимрадиусомкривизны;

4)длину волны падающего света уменьшают;

5)длину волны падающего света увеличивают.

11. Два когерентных луча приходят в некоторую точку

экрана с разностью фаз колебаний вектора E , равной δ. Выберите те δ, при которых в этой точке экрана будет свет (необязательно максимальный по интенсивности).

1) δ = 2; 2) δ = π; 3) δ = 32 π; 4) δ = 2π; 5) δ = 3π.

12. Какой путь пройдет фронт волны монохроматического света в вакууме за то же время, за которое он проходит 2,0 м в стекле (п = 1,5)?

1) 1,3 м; 2) 3,0 м; 3) 3,2 м; 4) 3,5 м; 5) задача неопределенна,

так как не задана длина волны света.

13. Свет от источника S приходит в точку Р, отразившись от дна стеклянного сосуда (пст = 1,5) и от границы раздела воздуха с водой (nв = 1,33) (рисунок). С какой оптической разностью хода лучи приходят в точку Р?

1) нуль; 2) 2а; 3) 4а; 4) λВ/2; 5) λ0/2 (λв и λ0 – соответственно длины волн в воде и вакууме).

147

a a S P

aa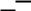

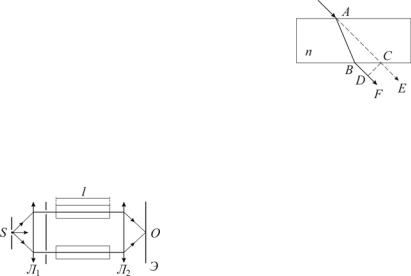
14.В опыте Юнга (рисунок) расстояние между щелями d =

=0,10 мм, расстояние от источников до экрана L = 2,0 м. Найдите длину волны монохроматического излучения, если расстояние от третьего интерференционного максимума до центральной полосы АО = 3,0 см.

1) 7,5·10–5 см; 2) 6,2·10–5 см; 3) 5,8·10–5 см; 4) 5,0·10–5 см; 5) 4,5·10–5 см.

15. Выберите из нижеприведенных выражений оптической разности хода двух лучей, пришедших в некоторую точку экрана от двух когерентных источников, те, при которых в данной точке экрана будет темнота.

148

16.На пути светового луча, идущего

ввоздухе по направлению АСЕ (рисунок), поставили плоскопараллельную пластинку с показателем преломления п, в результате чего луч пошел по направлению ABDF. На сколько изменилась при этом оптическая длина пути?

1) на ABn + BD – ACn; 2) на АBn – АС; 3) на ABn + BD – AC; 4) нa ABn + ВD + λ/2 – АС; 5) на ABn + BD + λ/2 – ACn.

17.Для измерения показателя преломления жидкости используют интерферометр Рэлея (рисунок). Узкая щель S освещается светом длиной волны λ = 0,550 мкм. Две одинаковые кюветы 1 и 2 длиной l = 2,0 см

были заполнены дистиллированной водой (п = 1,33018). На экране Э наблюдалась интерференционная картина. Когда воду в одной из кювет заменили раствором спирта, то интерференционная картина сменилась на 24 полосы. Определите показатель преломления раствора спирта.

1) 1,33084; 2) 1,34015; 3) 1,35120; 4) 1,38206; 5) 1,39101.

18. Изменится ли, если да, то как и во сколько раз, расстояние между соседними интерференционными полосами на экране

вопыте Юнга, если зеленый светофильтр заменить красным? (λзел = 500 нм, λкрасн = 700 нм).

1)не изменится; 2) уменьшится в 1,40 раза; 3) увеличится

в1,40 раза; 4) задача неопределенна, так как не задано расстояние между щелями и расстояние от щелей до экрана.

149

20. Из приведенных ниже выражений оптической разности хода двух лучей от двух когерентных источников, пришедших в некоторую точку экрана, выберите то, которое представляет собой условие максимума света в этой точке.

5)= 2(k + 1) 2. Здесь k = 0, 1, 2, 3 …

21.Для просветления линзы на нее наносят тонкую пленку

толщиной d с показателем преломления nпл, меньшим показателя преломления стекла пст. Какое из приведенных ниже условий должно выполняться для просветления линзы? Толщина пленки при этом должна быть минимальной.

1) 2dnпл = λ0; 2) 2dnпл = λ0/2; 3) dnпл = λ0; 4) 2dnст = λ0/2;

5)2d(nст – nпл) = λ0/2.

Здесь λ0 – длина волны желтого света, к которому глаз

наиболее чувствителен, λ0 = 0,55 мкм.

22. Щели в опыте Юнга освещают белым светом. Граничные длины волн спектров, получающихся на экране, λкр = 690 нм, λф = 420 нм. Сколько не перекрывающихся спектров можно наблюдать по одну сторону от центрального максимума?

1) один; 2) два; 3) три; 4) четыре; 5) пять.

150