
книги / Элементы прикладной теории надежности
..pdf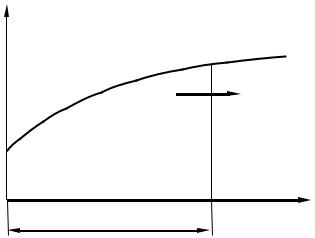
Отказ возникает, когда значение хотя бы одного параметра, характеризующего работоспособность, выходит за пределы установленного допуска. Поэтому условие неработоспособного состояния ТО может быть задано односторонним неравенством
yi > yiTT , i = 1,... m,
где yi – i-й параметр состояния ТО, характеризующий работоспособность; yiTT – технические требования к i-му параметру состояния ТО; m – число параметров состояния, установленных документацией.
Для примера (рис. 1) рассмотрим один из параметров, характеризующих работоспособность аксиально-плунжерного насоса, – зазор в сопряженной паре гильза-плунжер y (t ) .
y
y(t)
yTT |
|
|
|
|
отказ |
||
|
|
||
|
y(t) < yTT |
y(t) > yTT |
|
yн |
|
|
|
0 |
T – наработка до отказа |
|
t |
|
|
||
|
|
|
|
|
Рис. 1 |
|
|
Увеличение зазора приводит к росту утечек, снижению подачи насоса и КПД и в конечном итоге к отказу, критерий которого мо-
жет быть выражен неравенством y (t ) > yТТ, где yТТ – предельно допустимое значение зазора, установленное в документации.
11
Физически отказ является результатом процессов, происходящих в ТО под действием различных причин. Эти причины можно разделить на четыре группы:
1.Нарушение норм проектирования, технологии изготовления, правил и условий эксплуатации.
2.Скрытые дефекты, выявление которых требует специальных исследований.
3.Внешние воздействия (удары, вибрация, температура и т.п.), значения которых превышают расчетные.
4.Естественное старение и износ материалов.
2.2. Виды отказов
Различают следующие виды отказов (ГОСТ 27.002–2015). Полный отказ – работоспособность ТО утрачена полностью
(по всем параметрам технического состояния в соответствии с критерием отказа).
Частичный отказ – частичная потеря работоспособности по одному или нескольким параметрам технического состояния в соответствии с критерием отказа.
Зависимый отказ – отказ, обусловленный другими отказами. Независимый отказ – отказ, не обусловленный другими отка-
зами.
Внезапный отказ – отказ, характеризующийся скачкообразным изменением значений одного или нескольких параметров объекта.
Постепенный отказ – отказ, возникающий в результате постепенного изменения одного или нескольких параметров объекта.
Перемежающийся отказ – многократно возникающий самоустраняющийся отказ одного и того же характера.
Систематический отказ – отказ, однозначно вызванный определенной причиной, которая может быть устранена только модификацией проекта или производственного процесса, правил эксплуатации и документации.
Ресурсный отказ – отказ, в результате которого объект достигает предельного состояния.
12
Явный отказ – отказ, обнаруживаемый визуально или штатными методами и средствами контроля и диагностирования при подготовке объекта к применению или в процессе применения по назначению.
Скрытый отказ – отказ, не обнаруживаемый штатными методами и средствами контроля и диагностики, но выявляемый при проведении технического обслуживания или специальными методами диагностики.
Деградационный отказ – отказ, обусловленный естественным процессом старения, изнашивания, коррозии и усталости при соблюдении всех установленных правил и норм проектирования, изготовления и эксплуатации.
Конструктивный отказ – отказ, возникший по причине, связанной с несовершенством или нарушением установленных правил и норм проектирования и конструирования.
Производственный отказ – отказ, возникший по причине, связанной с несовершенством или нарушением установленных правил и норм производства (изготовления).
Эксплуатационный отказ – отказ, возникший по причине, связанной с нарушением установленных правил и условий эксплуатации.
2.3. Отказ как случайное событие
Понятие события
Событие – это исход опыта, испытания или наблюдения. Примером события может служить отказ фильтра. Возможны две причины отказа фильтра: 1. засорение фильтрующего элемента; 2. разрыв фильтрующего элемента. Продолжительность безотказной работы фильтра также считается событием, так как является исходом наблюдений или испытаний.
Событие, которое нельзя заранее предсказать, называется слу-
чайным событием.
Отказ фильтра – событие случайное, так как невозможно заранее предсказать время его появления. Это связано с тем, что в про-
13
цессе эксплуатации фильтр подвержен действию большого числа факторов, влияющих на его работоспособность: чистота рабочей жидкости (РЖ), давление, скорость, температура РЖ, механические воздействия и т.п. При этом они характеризуются достаточно большой степенью неопределенности.
Событие называется достоверным в данном опыте, если оно неизбежно происходит.
Например, при неограниченном времени эксплуатации фильтра в гидросистеме он когда-нибудь засорится, т.е. возникнет отказ – неработоспособное состояние. В данном опыте отказ – событие достоверное.
Событие называется невозможным в данном опыте, если оно заведомо не происходит.
Например, если через фильтр не протекает РЖ (таковы условия опыта), то он никогда не засорится.
Существует алгебра событий, в соответствии с которой события можно складывать и перемножать.
|
|
|
|
|
Произведение и сумма событий |
|
||||
|
|
Рассмотрим произведение и сумму двух событий. Пусть даны |
||||||||
событие A и событие B. |
|
|
|
|||||||
|
|
Произведением двух |
событий A B называется |
событие, со- |
||||||
стоящее в одновременном появлении как события A, |
так и собы- |
|||||||||
тия B. В этом случае события A и B являются совместными. |
||||||||||
ФУ |
|
|
|
|
|
|
Пример. Рассмотрим фильтрующее |
|||
|
Ф1 |
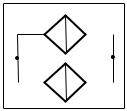
устройство (ФУ), состоящее из двух па- |
||||||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
раллельно соединенных фильтров (Ф1 и |
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Ф2) (рис. 2). |
|
|
|
|
|
Ф2 |
|
|
|||||
|
|
|
Пусть событие |
A – отказ (засоре- |
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
ние) Ф1; событие B – отказ (засорение) |
||
|
|
|
|
|
|
|
|
Ф2. Тогда событие |
A B |
– отказ ФУ |
|
|
|
Рис. 2 |
в целом. |
|
|
||||
14
События A и B называются несовместными в данном опыте, если появление одного из них исключает появление другого, а их произведение есть событие невозможное.
Под суммой двух событий A + B понимается событие, которое имеет место тогда, когда произошло хотя бы одно из них, т.е. произошло событие A или событие B, или события A и B одновременно.
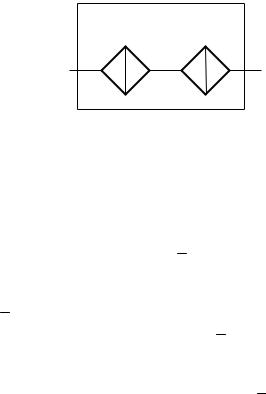
Пример. Рассмотрим фильтрующее устройство (ФУ), состоящее из двух последовательно соединенных фильтров (Ф1 и Ф2) (рис. 3).
ФУ
Ф1 Ф2
Рис. 3
Пусть событие A – отказ (засорение) Ф1; событие B – отказ (засорение) Ф2.
Тогда событие A + B в соответствии с определением – отказ Ф1 или Ф2, или Ф1 и Ф2 одновременно. Это отказ ФУ в целом.
Важное значение имеет понятие противоположного события.
Пусть дано событие A . Событие A , происходящее тогда, когда не происходит событие A , называется противоположным последнему.
Например, работоспособное состояние A и неработоспособное состояние A ТО являются противоположными событиями.
Сумма противоположных событий A + A – событие достоверное. ТО находится в одном из состояний: либо работоспособно, либо неработоспособно (иных состояний нет).
Произведение противоположных событий A A – событие невозможное. Одновременно находиться в работоспособном и неработоспособном состояниях ТО не может.
15

Вероятность случайного события
Пусть A – случайное событие. Для определения меры достоверности этого события вводят понятие вероятности наступления события:
вер( A) = P( A) .
Предполагается, что вероятность любого события заключается в диапазоне
0 ≤ P( A) ≤1.
Вероятность невозможного события равна нулю. Вероятность достоверного события равна единице.
В настоящее время формального определения вероятности не дается. Это понятие является первичным и не определяется.
При пояснении этого понятия его связывают с частотой события. Частота случайного события A в данной серии опытов – это отношение числа опытов, в которых появилось событие, к числу
произведенных опытов:
P ( A) = MnА ,
где n – число произведенных опытов; M А – число опытов, в кото-
рых событие A появилось.
Частота – характеристика опытная. Очевидно, что
0 ≤ P ( A) ≤1.
P ( A) =0 – событие A ни в одном опыте не появилось, событие невозможное.
P ( A) =1 – событие A появилось во всех опытах, событие достоверное.
При увеличении числа опытов n →∞ частота P ( A) колеблется около постоянного числа p , которое называется вероятностью события A в статистическом смысле.
16
Если известна вероятность появления события A в статистическом смысле p , то среднее число появления события A в n опытах
A = np .
Пример. Опытным путем установлено, что статистическая вероятность отказов насосов при наработке 500 ч
p = 0,05.
Можно утверждать, что из партии таких насосов в 2000 штук за 500 ч работы откажут в среднем
А = np = 2000 0,05 = 100 шт.
Произведение и сумма вероятностей событий
Поскольку случайные события можно умножать, складывать, то можно умножать и складывать вероятности этих событий.
Предварительно рассмотрим следующие определения.
1.Два события A и B называются независимыми, если вероятность каждого из них не зависит от появления или непоявления другого. В противном случае события будут зависимыми.
2.Вероятность события A при условии, что произошло событие
B , называется условной вероятностью события A и обозначается
P( A | B) = PВ ( A) .
Произведение вероятностей
Вероятность произведения двух зависимых событий A и B (т.е. вероятность одновременного появления событий A и B) равна
произведению вероятности одного из них на условную вероятность другого, в предположении, что первое имеет место, т.е.
P( A B) = P( A)PА(В) = P(В)PВ ( А).
Вероятность произведения двух независимых событий A и B равна произведению вероятностей этих событий:
P( A B) = P( A)P(В) .
17

Сумма вероятностей
Вероятность суммы двух несовместных событий (т.е. вероятность появления хотя бы одного из них) равна сумме вероятностей этих событий:
P( А+ В) = P( А) + P(В) .
Вероятность суммы двух совместных событий
P( А+ В) = P( А) + P(В) − P( А В) .
Отметим ряд важных положений.
1. Группа несовместных событий А, В,... называется полной, если в результате опыта обязательно появится одно из них. Для полной группы событий
P( А) + P(В) +…=1 .
2. Противоположные события образуют полную группу событий.
Пример. Работоспособное состояние А и неработоспособное состояние А ТО являются противоположными событиями и образуют полную группу событий. Поэтому
P( А) + P (А) =1.
Отсюда следуют важные соотношения
P( А) =1− P (А) и P(А) =1− P( А) ,
позволяющие вычислять вероятность события через вероятность противоположного события.
В прил. 2 рассмотрены примеры применения правил умножения и сложения вероятностей для определения вероятности безотказной работы гидравлических устройств.
18
3. ПОКАЗАТЕЛИ НАДЕЖНОСТИ ТЕХНИЧЕСКИХ ОБЪЕКТОВ
3.1. Основные понятия и определения
Рассмотрим следующие понятия и определения (ГОСТ 27.002– 2015).
Показатель надежности – количественная характеристика одного или нескольких свойств, составляющих надежность ТО.
Единичный показатель надежности – показатель надежности,
характеризующий одно из свойств, составляющих надежность ТО.
Комплексный показатель надежности – показатель надежно-
сти, характеризующий несколько свойств, составляющих надежность ТО.
Восстановление – это процесс перевода ТО в работоспособное состояние из неработоспособного состояния. Восстановление включает в себя идентификацию отказа (определение его места и характера), наладку или замену отказавшего элемента, регулирование и контроль технического состояния элементов ТО и заключительную операцию контроля технического состояния ТО в целом.
Ремонт – процесс перевода ТО в работоспособное состояние из предельного состояния, при котором происходит восстановление ресурса ТО в целом. В ремонт входят разборка, дефектовка, замена или восстановление отдельных деталей, узлов, элементов.
Невосстанавливаемые ТО – это ТО, восстановление работоспособности которых не предусмотрено документацией. Невосстанавливаемый ТО (элемент) работает до отказа, а затем может заменяться таким же ТО (элементом). При этом считается, что восстановление в условиях эксплуатации невозможно.
Восстанавливаемые ТО – это ТО, восстановление работоспособности которых предусмотрено документацией.
Понятия невосстанавливаемый и восстанавливаемый объект – относительны. Многие объекты на этапе хранения являются восстанавливаемыми, а на этапе применения по назначению – невосста-
19

навливаемыми (например, аппаратура летательных аппаратов, спутников: на этапе хранения – восстанавливаемая, в полете – невосстанавливаемая.)
3.2. Показатели надежности ТО
Некоторые сведения о случайных величинах
Под случайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение.
Случайная величина (СВ) может быть дискретной или непрерывной. Примером дискретной СВ является число отказов в некоторой совокупности однотипных ТО за время τ. Примером непрерывной СВ может служить время работы ТО до отказа.
Исчерпывающее представление о СВ дает закон распределения случайной величины. Это правило, устанавливающее соответствие между значениями СВ и их вероятностями.
Различают интегральный и дифференциальный законы распределения.
Интегральный закон распределения СВ – это функция действи-
тельной переменной x, которая определяет вероятность события X < x , где X – случайная величина:
F (x) = p( X < x).
Интегральный закон распределения устанавливает вероятность того, что СВ X принимает значения меньше x.
Дифференциальный закон распределения СВ (плотность рас-
пределения вероятности СВ, кратко – плотность распределения СВ) – это производная F (x) по x:
f (x) = dF (x) . dx
20
