книги / Числовые и степенные ряды. Ряды Фурье

Вычислим коэффициенты:

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

(2n + 2)(2n +1)cn+1 + cn = 0,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Преобразуем выражения для найденных коэффициентов. Умножимчислительи знаменателькаждойдробина2, получим

. . . . . . . . . . . . . . . . . . .

61

y′′ = 2 c2 + 3 2 c3 x + ... + n(n − 1) cn xn− 2 +

n=0

63

Получили коэффициент при xn :

(2n + 2)(2n +1)cn+1 + cn = 0.

Выразим коэффициент cn +1 :

Получили рекуррентную формулу для вычисления коэффициентов разложения. Из начальных условий следует, что

При n =2,3,… найдём соответствующие коэффициенты.

64

ГЛАВА 3. РЯДЫ ФУРЬЕ

3.1. Основные понятия

Определение 8. Функциональный ряд вида

с общим периодом 2π .

можно представить тригонометрическим рядом, сходящемся к данной функции:

sin (nx) ≤ 1 . Рассмотрим числовой ряд, составленный их коэффициентов тригонометрического ряда:

Следовательно, ряд (35) мажорируемый, его можно почленно интегрировать на отрезке [–π;π] .

Если 2π – периодическую функцию f (x) можно представить в видетригонометрическогоряда(36), товозникаютследующиевопросы:

1)Каким условиям должна удовлетворять функция, чтобы её можно было разложить в тригонометрический ряд?

2)Как найти коэффициенты разложения в тригонометрический ряд?

Вначале ответим на второй вопрос.

3.2. Нахождение коэффициентов тригонометрического ряда

Пусть 2π – периодическая функция f (x) задана на отрезке [–π;π] , тогда коэффициенты разложения в тригонометрический ряд можно вычислить по формулам

мулам (39)–(41), называются коэффициентами Фурье для функции f (x), тригонометрический ряд (35) – рядом Фурье.

3.3. Достаточное условие разложимости функции в ряд Фурье

Пусть 2π – периодическая функция f (x), задана на отрезке

[–π;π] .

Теорема 14 (Теорема Дирихле). Пусть 2π – периодическая функция f (x), на отрезке [–π;π] удовлетворяет двум условиям:

66

1)функция f (x) кусочно-непрерывна, т.е. непрерывна или имеет конечное число точек разрыва 1-го рода;

2)функция f (x) кусочно-монотонна, т.е. монотонна на всём

отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна.

Тогда соответствующий функции f (x) ряд Фурье сходится на этом отрезке и при этом

1) в точках непрерывности функции сумма ряда S (x) совпадает с самой функцией: S (x) = f (x) ;

2) в каждой точке x0 разрыва функции сумма ряда равна среднему арифметическому односторонних пределов:

удовлетворяет условиям 1 и 2 теоремы Дирихле, то её можно разложить в ряд Фурье

с коэффициентами, определяемыми по формулам (39)–(41). Поскольку исходная функция f (x) и сумма ряда Фурье являются пе-

риодическими функциями, то полученное разложение может быть получено во всей области определения функции.

Замечание

1. Теорема Дирихле даёт достаточное условие разложимости функции, но не необходимое. Существуют функции, не удовлетво-

67

ряющие условиям теоремы Дирихле, но разложимы в тригонометрический ряд Фурье.

2. Функция f (x) имеет период 2π : f (x) = f (x + 2π) = = f (x + 2πk).

Коэффициенты ряда Фурье можно вычислить по любому промежутку длины периода функции, если на нём выполнены условия теоремы Дирихле:

a0 = π1 a+ 2π f (x)dx,

a

an = π1 a+ 2π f ( x) cos(nx)dx,

a

bn = π1 a+ 2π f ( x) sin (nx)dx.

a

3. При вычислении коэффициентов будем использовать тот факт, что

sin(nπ) = 0 , cos(nπ) = (−1)n .

Пример 41. Разложить в ряд Фурье функцию f (x) периода 2π , заданную на отрезке [–π;π]:

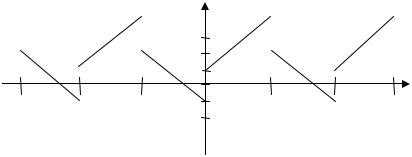
На рис. 1 изображен график функции.

Функция f (x) удовлетворяет условиям теоремы Дирихле. Найдём коэффициенты разложения:

68

Рис. 1

Вычислим неопределённый интеграл по частям:

69

=(x + 1) 1n sin (nx) − 1n sin (nx)dx =

=(x + 1) 1n sin (nx) − 1n sin (nx)dx =

=(x + 1) 1n sin (nx) + 1n 1n cos(nx) =

=1n (x + 1)sin (nx) + n12 cos(nx) + C.

Нашли неопределённый интеграл:

( x + 1) cos (nx)dx = 1n ( x + 1)sin (nx) + n12 cos (nx) + C.

Тогда

70