
книги / Численный расчёт стержневых систем
..pdf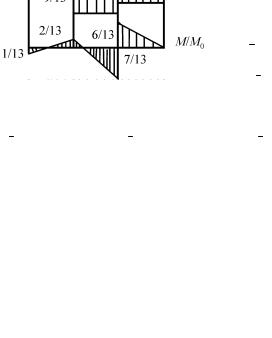
|
|
|
v5 |
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
= v(3) = v6 |
|
= |
M0l |
|
−4 . |
||
v |
||||||||||
|
|
|
||||||||
|
|
|
v |
|
|
26EJ |
0 |
|
||
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
2 |
||
|
|
|
8 |
|
|
|
|
|
|
|
Силы, действующие в концевых сечениях элементов, найдем по формуле P = kv:
P(1) |
|
|
|
3 |
|
P(2) |
|
|
|
−9 |
|
P(3) |
|
|
|
−6 |
||||||||||||||||
|
i y |
|
|
|
|
|
i y |
|
|
|
|
|
|
i y |
|
|
|
|
||||||||||||||
|
|
(1) |
|
|
|
l |
|
|
|
(2) |
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
||||||||
Mi z |
|
|
M0 |
|
Mi z |
|
|
M0 |
−2l |
|
Mi z |
|
|
M0 |
−6l |
|||||||||||||||||
|
|
|
|
|
= |
|
|
|
; |
|
|
|
|
) |
|
= |
|
|
9 |
|
; |
|
|
|
|
) |
|
= |
|
|
6 |
. |
|
1 |
|
13l |
2 |
13l |
3 |
13l |
|||||||||||||||||||||||||
|
( ) |
|
|
|
−3 |
|
|
( |
|
|
|
|
|
|
|
( |
|
|
|
|
|
|||||||||||
Pj |
|
|
|
|
|
|
|
|
Pj |
|
|
|
|
|
|
|
|
|
Pj |
|
|
|
|
|
|
|
|
|||||
y |
|
|
|
y |
|
|
|
−7l |
|
y |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||
M |
(1) |
|
|
|
|
|
|
M (2) |
|
|
|
|
|
|
|
M (3) |
|
|
|
|
|
|
||||||||||
|
|
j z |
|
|
|
|
|
|
|
|
|
j z |
|
|
|
|
|
|
|
|
|
|
j z |
|
|
|
|
|
|
|||
Рис. 4.4
Так как внеузловая нагрузка отсутствует, то в пределах каждого участка перерезывающие силы Q постоянны, а изгибающие моменты М изменяются по линейному закону. Эпюры Q и M представлены на рис. 4.4.
61
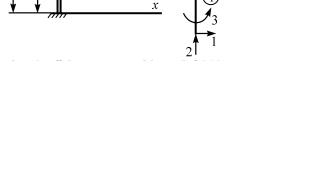
4.3. Расчет плоской рамы
Рассмотрим плоскую раму (рис. 4.5, а). Горизонтальный стержень нагружен равномерной нагрузкой q, а в середине вертикального действует сосредоточенная сила ql. Оба стержня имеют одина-
ковые площадь F и момент инерции J поперечного сечения относительно оси, перпендикулярной плоскости рамы. Схема нумерации и положительные направления узловых сил и перемещений показаны на рис. 4.5, б.
а б
Рис. 4.5
До сих пор при построении матрицы жесткости рамы учитывались осевые деформации стержней. Однако, как известно, влиянием осевых деформаций на перемещения в рамах можно пренебречь, если размеры поперечных сечений стержней достаточно малы по сравнению с их длинами. Полагая удлинения стержней равными нулю, можно упростить расчет, так как это позволяет снизить число неизвестных.
В самом деле, если считать стержни нерастяжимыми, то горизонтальное перемещение узла 2 следует приравнять к горизонтальному перемещению узла 3, а вертикальное – к вертикальному перемещению узла 1.
62
Так как узлы 1 и 3 неподвижны, то это равносильно требованию равенства нулю также и линейных перемещений узла 2. Таким образом, при использовании указанного упрощения неизвестным остается единственное перемещение v6 – угол поворота узла 2.
Следовательно, матрица неизвестных перемещений состоит из одного элемента: vα =[v6 ].
Поскольку внешний сосредоточенный момент в узле 2 отсутствует, то Pα =[P6 ] =[0] и равенство kααvα = Pα − P0α принимает вид
k66v6 = −P06.
Вычислим далее матрицы жесткости элементов 1 и 2 в местных
координатах, направив местную ось |
x |
|
в первом случае от узла 1 |
|||||||||||||||||
к узлу 2, а во втором – |
от узла 2 |
к узлу 3. |
По формулам (1.26) |
|||||||||||||||||
и (1.36) находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
(1) |
|
|
(2) |
= |
EF |
1 −1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
ka |
=k a |
l |
|
−1 |
|
; |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
12 |
|
6l |
|
−12 |
|
6l |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
6l |
|
4l |
2 |
|
−6l |
|
2l2 |
|
|
|
|
(1) |
|
|
(2) |
|
EJ |
|
|
|
|
|
||||||||
|
|
= |
|
|
|
|
. |
|||||||||||||
kb |
=kb |
l3 −12 −6l |
|
|
12 −6l |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
−6l |
|
4l2 |
|
|
|
|
|
|
|
|
|
|
|
|
6l |
|
2l |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матрицы P0 содержат уравновешивающие внеузловую нагрузку силы в направлении перемещений v: P0 ={P0a P0b}.
Подматрица P0a включает в себя силы, действующие вдоль
оси стержня. Так как внеузловые нагрузки вдоль осей x отсутствуют, то эти подматрицы для обоих стержней будут нулевыми.
Подматрицы P0b для рассматриваемых нагрузок определяются выражениями (2.4) и (2.5), где, учитывая направление нагрузок, следует сменить знаки на обратные и положить S = ql. В итоге имеем:
63
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
} |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
P |
0b |
|
= ql / 2 ql2 / 8 ql / 2 –ql2 / 8 , |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(2) |
|
|
|
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
} |
|
|
|
|
|
|
|
||||
|
|
|
|
P |
0b |
= |
|
|
|
ql / 2 |
|
ql2 /12 |
ql / 2 –ql2 /12 . |
|
|
|
|
|
|
||||||||||||||||||||||||||||
Координаты углов 1, 2 и 3 в общей системе координат равны |
|||||||||||||||||||||||||||||||||||||||||||||||
соответственно (0,0), |
|
(0,l ) |
и (l,l ). |
Пользуясь формулами (1.15), |
|||||||||||||||||||||||||||||||||||||||||||
находим матрицы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
λ |
(1) |
= |
|
λ |
|
|
λ |
|
|
|
(1) |
= |
[ |
0 1 ; |
|
λ |
(1) |
|
|
λ |
|
λ |
|
|
|
|
(1) |
= |
[ |
−1 0 |
] |
; |
|||||||||||||||
0 x |
|
xx |
xy |
|
|
|
|
0 y |
= |
yx |
|
yy |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
λ |
(2) |
= |
|
λ |
|
|
|
λ |
|
|
|
|
(2) |
= |
1 0 |
] |
; |
λ |
(2) |
= |
|
λ |
|
λ |
|
|
|
(2) |
= |
[ |
0 1 |
] |
. |
|
|||||||||||||
0 x |
|
xx |
xy |
|
|
0 y |
|
yx |
yy |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
[ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
В соответствии с (1.50) составляем матрицы преобразования |
|||||||||||||||||||||||||||||||||||||||||||||||
для каждого стержня: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
λ(a ) = |
|
0 1 |
|
| 0 | 0 0 |
| 0 |
|
|
; |
λ(a ) = |
|
1 0 | 0 | 0 0 | 0 |
; |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
| 0 | 0 1 |
| 0 |
|
|
|
|
|
|
|
|
|
| 1 0 | 0 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
|
0 0 | 0 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
−1 0 | 0 | |
|
0 0 | 0 |
|
|
|
|
0 1| 0 | |
|
0 0 | 0 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
λ(b1) = |
|
0 0 |
|
| 1| |
|
0 0 | 0 |
; |
λ(b2) = |
0 0 | 1| |
|
0 0 | |
0 . |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 0 | 0 | −1 0 | 0 |
|
|
|
|
0 0 | 0 | |
|
0 1| |
0 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 0 |
|
| 0 | |
|
1 0 | 1 |
|
|
|
|
|
|
0 0 | 0 |
| |
|
0 0 | 1 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По формуле (1.51) вычисляем матрицы жесткости элементов |
|||||||||||||||||||||||||||||||||||||||||||||||
в общей системе координат: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 0 −6l |
−12 0 6l |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ |
|
|
0 |
|
0 |
−γ |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
k(1) = |
|
EJ |
|
|
|
|
|
|
4l2 6l |
|
|
0 6l |
|
; |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
12 |
|
0 |
6l |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сим. |
|
|
|
|
γ |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4l |
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ 0 |
0 −γ |
0 |
0 |
|
|
|
|
|
|
|
12 |
6l 0 −12 6l |
|
|
||
|
|
|
|
|
|
||||
2 |
) = |
EJ |
|
|
4l2 0 −6l 2l2 |
||||
k( |
l3 |
|
|
γ |
0 |
0 |
|
. |
|
|
|
|
|
|
|
||||
|
|
|
сим. |
|
12 −6l |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4l |
2 |
|
|
|
|
|
|
|
|
|
|
|
здесь γ = Fl2 / J.
Наконец, согласно (2.3) находим:
(1) |
(1)т |
|
|
(1) |
|
(1)т |
|
|
|
(1) |
|
|
ql |
|
0 |
ql2 |
|
− |
ql |
0 – |
ql |
2 |
; |
||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
P0 |
= λa |
P0a |
+λb |
|
|
P0b = − |
2 |
|
8 |
|
2 |
8 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(2) |
(2)т |
|
(2) |
|
(2)т |
|
(2) |
= |
|
|
|
ql |
ql2 |
|
|
0 |
ql |
– |
ql2 |
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
P0 |
= λa |
|
P0a +λb |
|
|
P0b |
0 |
|
2 |
12 |
|
|
2 |
|
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|||||
Теперь имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
k66 = k66(1) +k66(2) = |
EJ3 (4l2 +4l2 ) |
= |
8EJ |
; |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
) |
= − |
ql |
2 |
ql2 |
= − |
ql2 |
. |
|
|
|
|
||||
|
|
|
|
P = P( ) |
|
+ P( |
|
+ |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
06 |
|
06 |
06 |
|
|
|
8 |
|
12 |
|
|
|
24 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляя |
k66 |
|
и |
|
P06 |
|
|
в уравнение |
|
k66v6 = −P06 , |
находим |
||||||||||||||||||
v6 = ql3 / (192EJ ).
Находим матрицы перемещений элементов 1 и 2:
– в общей системе координат:
v(1) = |
{ |
|
} |
; v(2) = |
{ |
|
|
|
/ (192EJ ) |
} |
||||
|
00000 ql3 / (192EJ ) |
|
00 ql3 |
000 ; |
||||||||||
– в местных координатах: |
|
|
|
{ |
|
|
} |
|||||||
|
|
(a1) |
a |
|
|
(b1) |
b |
|
|
|
|
|||
|
v |
= λ(1)v(1) ={00}; |
|
v |
= λ(1)v(1) |
= |
|
000 |
ql3 / (192EJ ) ; |
|||||
|
|
|
|
|
|
|
|
65 |
|
|
|
|
|
|
v(a2) = λ(a2)v(2) ={00}; v(b2) = λ(b2)v(2) ={ql3 / (192EJ ) 000}.
Узловые силы в местных координатах могут быть найдены по формуле (2.1), из которой следуют соотношения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pa = kava + P0a ; |
|
|
Pb = kbvb + P0b. |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
Отсюда имеем: |
|
( |
) |
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
={00}; |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pa |
|
|
= Pa |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
(1) |
|
|
|
|
(1) |
|
|
(1) |
|
|
|
(1) |
|
|
|
ql3 |
EJ |
{6l 2l2 |
−6l 4l2}+ |
ql ql2 |
ql |
|
ql2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
Pb |
−kb |
vb |
+ P0b |
= |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
− |
|
= |
|||||||||||||||||||||||||||||
|
192EJ |
|
l |
|
2 |
8 |
2 |
8 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
ql |
{51 13l 45 −10l }; |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
96 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
(2) |
|
|
(2) |
|
|
(2) |
|
|
(2) |
|
|
|
ql3 |
|
EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ql ql2 |
ql |
|
ql2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Pb |
−kb |
vb |
+ P0b |
= |
|
|
|
|
|
|
|
|
3 |
|
{6l |
4l2 |
−6l 2l2}+ |
|
|
|
− |
|
|
= |
|||||||||||||||||||||||||||
192EJ |
|
l |
|
2 |
12 |
2 |
12 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
ql |
{51 10l 45 −7l }. |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
96 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Напомним, что расположение элементов в матрицах Pb определяется соотношением Pb ={Pi y Mi z Pj y M j z }.
Далее вычисляем распределение изгибающих моментов и перерезывающих сил по длине каждого стержня и строим соответствующие эпюры (рис. 4.6).
(1) (2)
Матрицы Pa и Pa оказались нулевыми, т.е. в полученном
решении осевые силы в стержнях равны нулю вследствие принятого нами предположения о равенстве нулю вертикального и горизонтального смещений узла 2. Такое предположение равносильно наложению связей на узел 2 (рис. 4.7, а). Реакции наложенных опорных связей P4 и P5 (рис. 4.7, б) разгружают стержни, обеспечивая
равенство нулю их осевой деформации. Эти реакции можно найти из условий равновесия узла 2 (рис. 4.7, в):
66
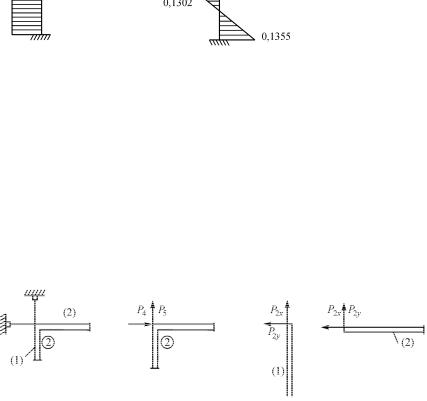
P4 = P2(x2) − P2(1y) = 0 − 9645 ql = −0, 469ql;
P5 =P2(1x) + P2(y2) = 0 + 9651 ql = 0,531ql.
Рис. 4.6
а |
б |
в |
Рис. 4.7
Поскольку в действительности силы P4 и P5 отсутствуют,
в узле 2 следует приложить равные им и противоположно направленные силы, которые вызовут появление осевых сил в стержнях рамы. Горизонтальная сила будет равна 0,469ql и вызовет сжатие
стержня 2, вертикальная сила составит 0,531ql и вызовет сжатие стержня 1.
67
Данные примеры рассмотрены с иллюстративной целью. Преимущества матричного метода перемещений выявляются при расчете сложных многократно статистически неопределимых систем. Эти преимущества обусловлены однообразием вычислений, которые могут быть эффективно выполнены с помощью вычислительной техники.
68
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Галлагер Р. Метод конечных элементов. Основы: пер.
сангл. – М.: Мир, 1984. – 428 с.
2.Зенкевич О., Чанг И. Метод конечных элементов в теории сооружений и механике сплошных сред: пер. с англ. – М.: Недра, 1974. – 295 с.
3.Зенкевич О. Метод конечных элементов в технике: пер.
сангл. – М.: Мир, 1975. – 541 с.
4.Зенкевич О., Морган К. Конечные элементы и аппроксима-
ция: пер. с англ. – М.: Мир, 1986. – 318 с.
5.Образцов И.Ф., Савельев Л.М., Хазанов Х.С. Метод конечных элементов в задачах строительной механики летательных аппаратов: учеб. пособие. – М.: Высшая школа, 1985. – 392 с.
6.Писаренко Г.С. Сопротивление материалов. – Киев: Выща школа, 1986. – 775 c.
7.Феодосьев В.И. Сопротивление материалов. – М.: Наука, 1986. – 612 с.
8.Дарков А.В., Шапошников Н.Н. Строительная механика. – М.: Высшая школа, 1989. – 607 с.
9.Мячников В.И. Расчет машиностроительных конструкций методом конечных элементов. – М.: Машиностроение, 1989. – 520 с.
69

Учебное издание
СУХОДОЕВА Алла Алексеевна
ЧИСЛЕННЫЙ РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ
Учебное пособие
Редактор и корректор Е.В. Копытина
Подписано в печать 23.08.13. Формат 60×90/16. Усл. печ. л. 4,5. Тираж 100 экз. Заказ № 179/2013.
Издательство Пермского национального исследовательского
политехнического университета.
Адрес: 614990, г. Пермь, Комсомольский пр., 29, к. 113.
Тел. (342) 219-80-33.
70
