
книги / Численный расчёт стержневых систем
..pdf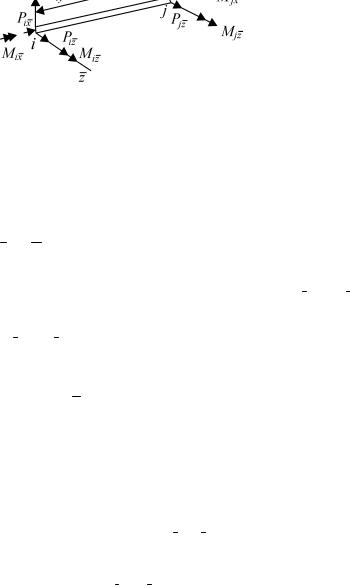
Рис. 1.8
узла j. Однако здесь удобнее расположить перемещения и силы
в матрицах v и P в ином порядке. При выбранной системе местных осей узловые силы распадаются на четыре группы, которые можно рассматривать независимо друг от друга. Силы Pi x и Pj x
вызывают только осевую деформацию бруса и определяются перемещениями vi x и vj x . Образуем из них соответствующие подмат-
рицы:
|
P |
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|||||
Pa = i x |
; va = i x |
|||||||||
|
Pj |
|
|
vj |
|
|
||||
|
x |
x |
||||||||
|
|
|
|
|
|
|
||||
.
Эти подматрицы связаны между собой равенством
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.21) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pa = kava , |
||||
где |
|
|
|
|
– некоторая квадратная матрица размером 2×2. |
||||||||||||||||
ka |
|||||||||||||||||||||
|
|
|
Силы Pi |
|
, Pi |
|
, а также моменты Mi z , Mi z вызывают изгиб бруса |
||||||||||||||
|
|
|
y |
y |
|||||||||||||||||
только |
в плоскости |
|
|
|
и |
определяются |
только перемещениями |
||||||||||||||
x |
y |
||||||||||||||||||||
vi |
|
, vj |
|
|
и углами поворота |
θi z , θj z . Составим из этих компонент |
|||||||||||||||
y |
y |
||||||||||||||||||||
подматрицы:
21
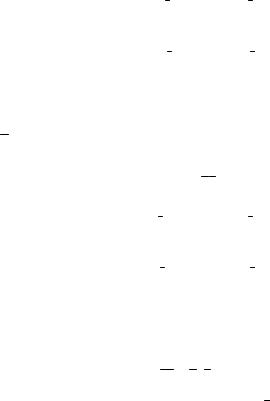
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
i y |
|
|
|
|
|
|
|
|
|
i y |
||||||||||
|
|
Mi z |
; |
|
|
|
|
|
|
θi z |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
Pb = |
P |
|
|
|
|
|
vb = |
v |
|
|
|
|
. |
|||||||||
|
|
|
j y |
|
|
|
|
|
|
|
|
|
|
j y |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M j z |
|
|
|
|
|
|
|
θj z |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Связь между ними снова представим в форме |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
P |
b = |
k |
b |
v |
b , |
|
|
(1.22) |
|||||||||||
где kb – квадратная матрица размером 4×4.
Аналогично образуем подматрицы сил и перемещений, опре-
деляющих изгиб бруса в плоскости xz :
|
P |
|
|
|
|
|
|
|
v |
|
|
|
|
|
||
|
|
i z |
|
|
|
|
|
|
|
|
i z |
|
|
|||
|
Mi |
|
|
|
|
|
|
|
θi |
|
|
|
|
|||
|
y |
; |
y |
|||||||||||||
|
|
|||||||||||||||
Pc = |
P |
|
|
|
|
vc = |
v |
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
j z |
||||||
|
j z |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M j |
|
|
|
|
|
θj |
|
|
|||||||
|
y |
|
y |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соответствующую матрицу жесткости обозначим kc , получим:
Pc = kc vc .
Наконец, кручение стержня вокруг оси матрицы:
|
M |
|
|
|
|
|
|
θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Pd = |
i x ; |
vd = |
i x |
||||||||||
|
M j |
|
|
|
θj |
|
|
||||||
|
x |
|
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.23)
x характеризуют под-
.
Они связаны соотношением
P |
d = |
k |
d |
v |
d . |
(1.24) |
22
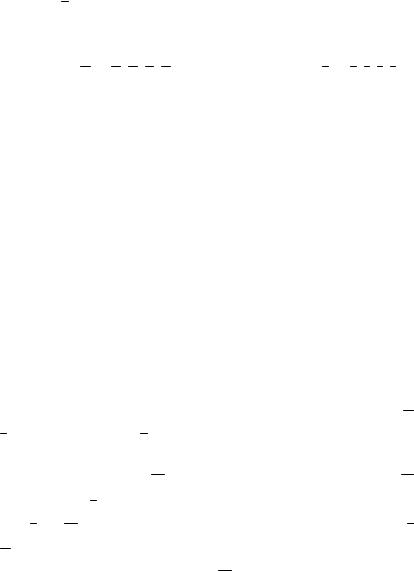
Здесь kd еще одна подлежащая отысканию матрица размером 2×2.
В совокупности формулы (1.21)–(1.24) дают связь между узловыми силами P = {Pa Pb Pc Pd }т и перемещениями v = {va vb vc vd }т
рассматриваемого конструктивного элемента. Объединим эти формулы общим равенством
|
|
a |
|
|
|
a 0 0 0 |
|
|
|
a |
|||||||||||||||
P |
k |
v |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Pb |
0 kb 0 0 |
vb |
|||||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Pc |
0 0 kc 0 |
vc |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Pd |
0 0 0 kd |
vd |
|||||||||||||||||||||||
Оно имеет стандартную форму |
|
|
= |
|
|
|
|
||||||||||||||||||
P |
kv. |
|
|||||||||||||||||||||||
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||||||||||||||
|
|
|
|
ka |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
kb |
|
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
k = |
|
|
|
|
|
|
|
|
|
|
|
. |
(1.25) |
||||||||||
|
|
|
|
|
kc |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
kd |
|
|||||||||||
Таким образом, при выбранном расположении компонент P
и v матрица жесткости k оказывается блочно-диагональной. Переходя к вычислению отдельных блоков матрицы жестко-
сти, начнем с матрицы ka . Эта подматрица связывает силы Pa и перемещения va равенством (1.21). Перемещения и силы в матрицах va и Pa расположены в том же порядке, что и в матрицах v
и P для ферменного элемента, и определяют они деформацию бру-
са вдоль оси. Поэтому подматрица ka совпадает с матрицей жесткости (1.14) ферменного элемента в местной системе координат:
23
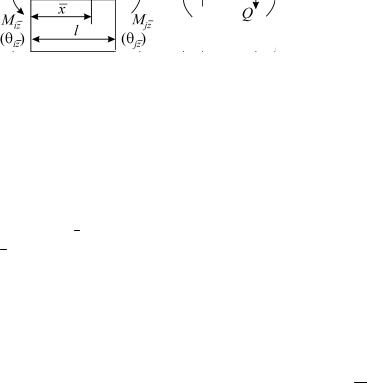
|
|
|
|
|
|
|
|
|
|
|
|
|
EF |
|
1−1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
ka = |
(1.26) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
l |
|
−1 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||
|
Для вычисления подматрицы |
|
|
необходимо рассмотреть из- |
||||||||||||||||||
|
kb |
|||||||||||||||||||||
гиб бруса в плоскости |
|
|
|
(рис. 1.9, а). Пусть u |
|
|
– прогиб бруса на |
|||||||||||||||
x |
y |
|||||||||||||||||||||
|
y |
|||||||||||||||||||||
расстоянии |
|
от левого конца. |
Введем безразмерную координату |
|||||||||||||||||||
x |
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||
ξ = |
2x |
−1, которая изменяется от –1 в узле i до +1 в узле j. |
||||||||||||||||||||
|
||||||||||||||||||||||
|
l |
|
|
|
|
|
|
|
|
|
||||||||||||
а |
б |
|
Рис. 1.9 |
Если на концах бруса заданы поперечные смещения и углы поворота, то изогнутая форма бруса будет однозначно определена. Другими словами, в соответствии с технической теорией изгиба балки прогиб uy однозначно определяется узловыми перемещения-
ми vb . В матричных обозначениях это означает существование равенства
|
|
(ξ) = N (ξ) |
|
b , |
(1.27) |
u |
|
v |
|||
y |
где N (ξ) – матрица-строка, четыре элемента которой являются функциями координаты ξ. Эта матрица будет в явной форме полу-
чена ниже, а сейчас перейдем к вычислению подматрицы kb , считая, что матрица N (ξ) известна.
24
Выпишем известные из курса сопротивления материалов дифференциальные соотношения для изгиба балки постоянной же-
сткости в плоскости xy:
|
d 2u |
|
|
|
dM |
|
d 3u y |
|
dQ |
|
d 4u |
|
|
|
|
|
|
|
|
|
y |
|
|
||||||
y |
|
|
|
|
||||||||||
M = EJz |
|
; |
Q = d x |
= EJz |
|
; |
q = d x |
= EJz |
|
|
, |
|||
dx 2 |
d x3 |
d x 4 |
|
|||||||||||
где Jz – момент инерции поперечного сечения относительно оси z;
М – изгибающий момент в сечении балки; Q – перерезывающая сила; q – погонная поперечная нагрузка.
Положительные направления Q и М показаны на рис. 1.9, б, а положительная нагрузка q действует по оси y. Такое правило зна-
ков для М, Q и q при выбранной системе координат определяет положительные знаки в записанных выше формулах.
Переходя к дифференцированию по ξ, перепишем данные соотношения в следующем виде:
M = |
4EJz |
u′′ |
(ξ) ; Q = |
8EJz |
u′′′(ξ) ; uIV (ξ) = |
ql4 |
. (1.28) |
||
|
l2 y |
|
|
l3 |
y |
y |
16EJ |
|
|
|
|
|
|
|
|
|
|
z |
|
На концах балки (при |
ξ = −1 |
и |
ξ =1) изгибающий момент |
||||||
и перерезывающая сила должны совпадать с их узловыми значениями. Учитывая направления сил и моментов, показанные на
рис. 1.9, запишем: |
|
Pi |
|
|
=Q(−1) ; |
Mi z = −M (−1) ; |
Pi |
|
= −Q(1) ; Mi z = |
|||||||||||||
|
y |
y |
||||||||||||||||||||
= M (1) . Подставим в эти равенства соотношения (1.28): |
||||||||||||||||||||||
Pi |
|
= |
8EJ |
z |
|
u |
′′′y (−1); |
Mi z |
= − |
|
4EJ |
z |
|
u′′y |
(−1); |
|||||||
y |
3 |
|
|
2 |
|
|||||||||||||||||
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
l |
|
|
|
(1.29) |
||||
|
|
|
|
|
8EJ |
|
|
|
|
|
|
4EJ |
|
|
|
|||||||
Pi |
|
= − |
|
z |
u |
′′′y (1); |
Mi z |
= − |
|
z |
|
u′′y |
(1). |
|||||||||
y |
|
3 |
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
25

С учетом (1.27) получаем отсюда следующую связь между узловыми силами и узловыми перемещениями:
|
|
|
|
|
|
|
= 8EJz |
N′′′(−1) |
|
|
; |
|
|
|
= − |
4EJz |
N′′(−1) |
|
b ; |
||||||||||||
|
|
|
|
P |
|
|
vb |
|
M |
|
v |
||||||||||||||||||||
|
|
|
i z |
l2 |
|
||||||||||||||||||||||||||
|
|
|
|
i y |
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.30) |
|||||
|
|
|
|
|
|
|
= −8EJz N′′′(1) |
|
|
|
|
|
|
|
|
4EJz |
|
N′′(1) |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
; |
|
|
|
= |
|
|
b. |
|
|||||||||||||||
|
|
|
|
P |
|
|
vb |
|
M |
i z |
v |
|
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
i y |
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
||||
|
|
В матричной записи эти формулы имеют стандартный вид |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Pb = kbvb , где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8N′′′(−1) |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
|
−4lN′′(−1) |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
kb = |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
−8N′′′(1) |
. |
|
|
|
|
|
|
|
(1.31) |
|||||||||
|
|
|
|
|
|
|
|
l |
3 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4lN′′(1) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Таким образом, |
для формирования матрицы |
|
|
необходимо |
|||||||||||||||||||||||||
|
|
kb |
|||||||||||||||||||||||||||||
определить матрицу-строку N (ξ) и воспользоваться формулой
(1.31).
Для отыскания матрицы N (ξ) обратимся к последнему соот-
ношению (1.28). Здесь рассматривается изгиб бруса под действием одних лишь узловых сил и моментов. В соответствии с этим пола-
гая q = 0, запишем: uyIV (ξ) = 0. Решение этого однородного дифференциального уравнения имеет вид
u |
|
(ξ) =C1 +C2ξ+C3ξ2 +C4ξ3 , |
(1.32) |
y |
где C1 , …, C4 – произвольные постоянные, подлежащие определению из граничных условий. Последние заключаются в том, что на левом конце балки прогиб uy должен равняться ui у , а угол поворо-
та |
duy |
= |
2 duy |
должен равняться |
θ |
|
|
|
; |
аналогичные соотношения |
|||
|
|
|
|
|
|
|
|||||||
d x |
l dξ |
i x |
|||||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
имеют место на правом конце. Таким образом, решение (1.32) необходимо подчинить следующим условиям:
u |
|
(−1) = vi |
|
; |
2 |
uy (−1) =θi z ; u |
|
(1) = vi |
|
; |
2 |
uy (1) = θi z . (1.33) |
|
|
|
|
|||||||||
y |
y |
y |
y |
|||||||||
|
|
|
|
|
l |
l |
||||||
Дифференцируя (1.32) по ξ, находим: u′y (ξ) =C2 +2C3ξ+3C4ξ2.
На основании (1.33) приходим к уравнениям:
C1 −C2 +C3 −C4 = vi |
|
; |
C1 +C2 +C3 +C4 = vi |
|
; |
|||||||||||
y |
y |
|||||||||||||||
|
|
−2C +3C |
|
= 1 |
θ |
|
|
|
|
|
+2C +3C |
|
= 1 |
|
|
(1.34) |
C |
2 |
4 |
|
|
; |
C |
2 |
4 |
θ . |
|||||||
|
3 |
2 |
|
i z |
|
|
3 |
2 |
i z |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Решая эту систему, находим:
C1 = 12 (vi y +vj y )+ 8l (θi z −θj z ); C2 = − 34 (vi y −vj y )− 8l (θi z +θj z ) ;
C3 = −8l (θi z −θj z );
C4 = 14 (vi y −vj y )+ 8l (θi z +θj z ) .
После подстановки постоянных в (1.32) получим уравнение изогнутой оси бруса:
uy = 14 (2 −3ξ+ξ3 )vi y + 8l (1−ξ−ξ2 +ξ3 )θi z + 14 (2 +3ξ−ξ3 )vj y −
−8l (1+ξ−ξ2 −ξ3 )θj z .
Вматричной форме это выражение имеет требуемый вид:
uy = N (ξ)vb ,
27

где
N (ξ) = 1 |
(2 −3ξ+ξ3 ) |
|
l |
(1−ξ−ξ2 |
+ξ3 ) → |
|||||
8 |
||||||||||
|
|
4 |
|
|
|
|
|
|||
→ |
1 |
(2 +3ξ−ξ3 ) |
l |
(−1−ξ+ξ2 +ξ3 ) . |
||||||
4 |
8 |
|
||||||||
|
|
|
|
|
|
|
|
|||
Дифференцируя последнее равенство, получим:
N ′′(ξ) = |
3 |
ξ 1 (−1+3ξ) |
− |
3 |
ξ |
|
|
1 (1 |
+3ξ) |
; |
||||||||
|
|
|
|
|
|
|||||||||||||
|
4 |
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
N ′′′(ξ) = |
3 |
|
3 |
l |
− |
3 |
|
3 |
l |
. |
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
4 |
|
2 |
|
|
4 |
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
По формуле (1.31) получаем искомую матрицу:
|
|
|
|
12 |
6l |
−12 |
6l |
|
|
|
|
|
|
|
6l |
4l2 −6l 2l2 |
|
|
|||
|
|
EJz |
|
|
||||||
kb = |
. |
|||||||||
l3 |
|
−12 |
−6l |
12 −6l |
|
|||||
|
|
|
||||||||
|
|
|
|
|
2l2 −6l |
4l2 |
|
|
||
|
|
|
6l |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
(1.35)
(1.36)
Далее рассмотрим изгиб бруса в плоскости xz (рис. 1.10). В этой плоскости положительные узловые моменты (а также углы поворота) направлены по сравнению с предыдущим случаем (см. рис. 1.9) в противоположную сторону. В остальном обе схемы идентичны.
Повторяя предыдущие выкладки, найдем подматрицу
|
|
|
|
|
12 |
−6l −12 −6l |
|
|
|||||
|
|
EJ |
|
|
|
−6l |
4l2 |
6l |
2l2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
y |
|
|
|||||||||
kc = |
, |
(1.37) |
|||||||||||
|
|
|
|
−12 |
|
|
|
|
|||||
l3 |
|
|
6l |
12 6l |
|||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
−6l |
2l2 |
|
4l2 |
|
|
|
|
|
|
|
|
|
|
6l |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где J y – момент инерции сечения бруса относительно оси y.
28
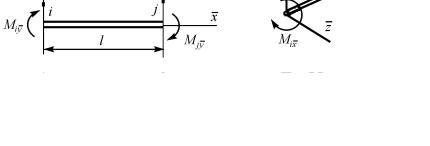
Рис. 1.10 |
|
|
Рис. 1.11 |
||
Рассмотрим, наконец, кручение бруса (рис. |
1.11). Сечение j |
||||
относительно сечения i закручивается на угол |
θj |
|
−θi |
|
. Из курса |
x |
x |
||||
сопротивления материалов известно, что крутящий момент в сечении бруса, необходимый для создания такого угла закручивания,
|
|
|
GJкр |
(θj |
|
|
|
|
|
|
|
) = |
|
GJкр |
|
|
|
|
|
θ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
M j |
|
= |
|
|
|
−θi |
|
|
[−11] |
i x , |
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
x |
x |
x |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
θj |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где GJкр – жесткость стержня на кручение. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Из уравнения равновесия имеем также: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
GJкр |
|
|
θ |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
M |
|
|
|
= −M |
|
|
|
|
= |
[1 −1] |
i x |
. |
|
|
|
|
|
||||||||||
|
|
i x |
j x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
l |
|
|
θj |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Объединяя эти соотношения в одно матричное равенство, получаем:
|
|
|
|
|
|
|
Pd = |
k |
d |
v |
d , |
(1.38) |
|
|
|
GJ |
кр |
|
1 |
−1 |
|
||||
где kd = |
|
|||||||||||
|
|
|
. |
|
||||||||
|
|
−1 |
|
|||||||||
|
|
|
l |
|
|
1 |
|
|||||
Формулами (1.25), (1.26), (1.36), (1.37) и (1.38) определяется матрица жесткости бруса постоянной жесткости в местной системе координат.
29
Теперь балочный элемент будем рассматривать в общей системе координат. В этой системе координат матрицу v(e) образуем, перечисляя, как обычно, сначала перемещения узла i, а затем – узла j. В свою очередь, в каждом узле условимся перечислять сначала
линейные смещения, а затем угловые. Обозначим матрицы линейных и угловых перемещений узла i:
|
|
|
|
|
|
|
|
|
v* = |
vvix |
; |
θ |
i |
= |
θθix . |
||
i |
|
iy |
|
|
|
|
iy |
|
|
v |
|
|
|
|
θ |
|
|
|
|
iz |
|
|
|
|
|
iz |
Тогда матрица перемещений узла i
v*
vi = i .
θi
Аналогичные обозначения введем для перемещений узла j.
Матрица узловых перемещений всего бруса в общей системе координат будет иметь следующую блочную форму:
vi* v(e) = vvi = θv*i .
j jθj
Подобным же образом составим матрицу узловых сил P(e) , перечисляя сначала силы и моменты в узле i:
Pix(e)
Pi* = Piy(e)
Piz(e)
|
|
M |
|
|
|
|
; |
Mi = M |
|
|
|
|
|
M |
|
|
|
(e) ix
(e) iy
(e) iz
;
P* |
|
Pi(e) = i |
. |
Mi |
|
|
|
Пользуясь подобными обозначениями для узла j, запишем:
30
