Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

книги / Теоретические основы автоматизированного управления.-1

.pdf

Скачиваний:

Добавлен:

20.11.2023

Размер:

696.22 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Разложим выражение (13.5) для Ψ(jω) на простые дроби:

( j )

где

i 1

( j ) .

Найдем функцию γ(t) вида

(t)

( j )e j t d .

Подставляя (13.7) в (13.9), получим

e j t d ,

(t)

причем

i 1

e j t d die j it .

2 j

Поэтому

(t) j die j it .

Введем в рассмотрение функцию

i 1

(t) 0,

t 0

(t) (t t0 ) jdie j i (t t0 ) , t

i 1

и вычислим соответствующее ей преобразование Фурье

(13.7)

(13.8)

(13.9)

(13.10)

(13.11)

	j t		j t	j i (t t0 )		di		j it0
B( j ) e		(t)dt e	jdie	dt			e		. (13.12)
B( j ) e		(t)dt e	jdie	dt		i	e		. (13.12)
0		0	i 1		i 1	i

Итак, если все полюсы Sm(ω) – простые, то определим ( j ) по формуле

			di		e j it0
	B( j )
			i
( j )		i 1				.	(13.13)
	( j )			di

i 1 i

Предположим теперь, что некоторые из полюсов функции Sm(ω) являются кратными.

Тогда каждому полюсу кратности χ в разложении функции Ψ(jω) на простые дроби будет соответствовать выражение

(13.14)

i 2

где

d 1

( j ) .

(

1)!

d 1

Соотношение для Bi(jω) имеет вид

( j ) a

e j it0 1

( jt0 )

(13.15)

( 1 )!

( i ) 1

Таким образом, каждый кратный полюс с кратностью χ дает член вида (13.15) в числителе выражения для оптимальной передаточной функции.

Если, например, все полюсы – простые, за исключением одного кратного полюса λi с кратностью χ, то

	a e j rt0	1	a e j it0 1 ( jt0 )			1	1

	r 1 r		1 i	0
( j )	r 1 r	r	1 i	0	( 1 )!		( i ) 1	.	(13.16)
( j )				( j )				.	(13.16)
				( j )

Минимальное среднее значение квадрата ошибки упреждения (показатель точности системы упреждения) определяется соотношением

min2	t0	2 (t)dt .

	0

Для полюса λi кратности χ определим γi(t). Имеем

(t)

j t 1

( 1)!

(13.17)

(13.18)

Решение типовых задач

Задача 13.1. Дано
		2	2
Sm	( )			.
Sm	( )	2 2	2 2	.
		2 2	2 2

Определить оптимальную передаточную функцию Φ(jω) прогнозирующего фильтра.

Решение. Запишем Sm(ω) в виде

				2	2
	Sm ( )
	Sm ( )		2	2 2 2	2 2 2 2
			2	2 2 2	2 2 2 2
Отсюда имеем
Sm ( )	2	2 2		2 2 2 2 2 2 2
Sm ( )		2 2 2 2 2 2 2 2
		2 2 2 2 2 2 2 2

или
2 2		2 2 2 2
Sm ( ) 2 2	2 2	2 2 2 2 .

Определим корни 1-го сомножителя в знаменателе Sm(ω). Имеем

Откуда получим		2 2 2 2 0 .
Откуда получим
		2 4 2 4 2 4 2
				j .
				j .
1,2		2
Следовательно		2
Следовательно	1 j ;		2 j .
	1 j ;		2 j .

Определим корни 2-го сомножителя в знаменателе Sm(ω). Имеем

2 2 2 2 0 .

Откуда получим
		2 4 2			4 2 4 2
3,4									j .
3,4					2				j .
Следовательно					2
Следовательно	3 j ;					4 j .
Введем обозначения	3 j ;					4 j .
Введем обозначения	j ;					2 j ;
1	j ;					2 j ;					(13.19)
Тогда
1 1;			3 2 ;			2 2 ;				4 1 .
Запишем Sm(ω) в виде
Sm ( )			2 2 2 2 2 2
Sm ( )			( 1 )( 3 )( 2 )( 4 )
или			( 1 )( 3 )( 2 )( 4 )
или
Sm ( )			2 2		2			2 2			2
Sm ( )		( 1 )( 2 )						( 1 )( 2 )
		( 1 )( 2 )						( 1 )( 2 )
Отсюда с учетом (13.4), (13.5) получим
	( j )					A1				,	(13.20)
где	( j )			( 1 )( 2 )						,	(13.20)
где
			A 2			2	2 .
		1

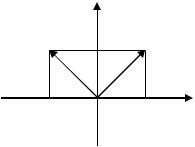
Ψ(jω) содержит полюсы в верхней полуплоскости. Действительно

λ1

jα

λ2

-β

Рис. 13.2

Представим Ψ(jω) в виде

( j )

(d1 d2 ) ( d1 2

d2 1 )

(13.21)

( 1 )( 2 )

Из (13.20), (13.21) получим

d1 d2 0;

d1 2 d2 1 A1.

Определим d1, d2 по правилу Крамера. Имеем

2 ;

A ;

;

d2 d1

Из (13.13) получим

e j 1t0

e j 2t0

( j )

или

e j 1t0

e j 2t0

( j )

Перепишем Φ(jω) в виде

( 1 )( 2 )

( j )

d1 ( 2 )e j 1t0

d2 ( 1 )e j 2t0 .

(13.22)

В экспоненты e j 1t0 , e j 2t0 подставим λ1 и λ2. С учетом (13.19) имеем

e j 1t0

e j( j )t0

e t0 cos t0 j sin t0 ;

e j 2t0

e j( j )t0

e t0

cos t0

j sin t0 .

Подставим полученные выражения в формулу (13.22). Получим

( j ) e t0

d1 ( 2 )(cos t0 j sin t0 ) d2 ( 1 )(cos t0

j sin t0 )

или

( j ) e t0

(d1 d2 ) (d1 2 d2 1 ) cos t0

( d1

d2 ) (d1 2

d2 1 ) jsin t0

Подставим в полученную формулу d1, d2, λ1, λ2. Имеем

( j ) e

sin t

( j )

cos t

или

( j ) e t0 a( j ) b ,

где

a1 sin t0 ;

bcos t0 sin t0 .

Задачи для самостоятельного решения
Задача 13.2. Дано			2Dm
		Sm ( )	2Dm			.
		Sm ( )	2	2		.
			2	2
Определить оптимальную передаточную функцию Φ(jω) прогнози-
рующего фильтра.
Задача 13.3. Дано
		1				1
Sm	( )						.
Sm	( )	2 ( )2			2 ( )2		.
		2 ( )2			2 ( )2

Определить оптимальную передаточную функцию Φ(jω) прогнозирующего фильтра.

Задача 13.4. Дано

Sm ( )		1		.
	4	2 2	4

Определить оптимальную передаточную функцию Φ(jω) прогнозирующего фильтра.

Указание. Представить знаменатель Sm(ω) в виде

4 2 2 4 ( j )4 2( j )2 4 ( j )2 A ( j ) 2 ( j )2 A ( j ) 2

( j )4 (4 A2 ) ( j )2 4
Определить А:
4 A2 2;						A2 6;				A 6.
Найти корни полинома ( j )2				6 ( j ) 2:
( j )2 6 ( j ) 2 0;
( j )1,2					3 j		;
( j )1,2					2		;
					2
( j )1			3 j			;	( j )2				3 j			.
( j )1						;	( j )2							.
Отсюда					2							2
Отсюда
	1 j			3	;			2	1 j			3	.
					;								.
1		2			1					2		2
		2								2

Записать Ψ(jω).

Задача 13.5. Дано

Sm ( ) 41 1.

Определить оптимальную передаточную функцию Φ(jω) прогнозирующего фильтра.

Указание. Представить знаменатель Sm(ω) в виде

4 1 ( j )4 1 ( j )2 A ( j ) 1 ( j )2 A ( j ) 1

( j )4 (2 A2 ) ( j )2 1

Определить А:

2 A2 0;

A2 2;

A 2.

Найти корни полинома ( j )2 2 ( j ) 1:


( j )2 2 ( j ) 1 0;
( j )1,2		1 j		;

2
( j )1	1 j		;	( j )2	1 j	.
					2
2

Отсюда

1 j			;	2	1 j	2	.
1	2	1		2	2	2
	2				2

Записать Ψ(jω).

Задача 13.6. Дано

Sm ( ) ( 2 1 1)2 .

Определить оптимальную передаточную функцию Φ(jω) прогнозирующего фильтра.

Указание. Использовать формулы (13.14), (13.15) при σ = 2.

Задача 13.7. Дано

Sm ( ) ( 2 1 1)3 .

Определить оптимальную передаточную функцию Φ(jω) прогнозирующего фильтра.

Указание. Использовать формулы (13.14), (13.15) при σ = 3.

Задача 13.8. Дано

Sm ( )	2(	2 2 )	,
	( )2 2	( )2 2

где λ ≥ β.

Определить оптимальную передаточную функцию Φ(jω) прогнозирующего фильтра.

Практическое занятие №14. Методы теории информации

Теоретические сведения

Любое сообщение, с которым мы имеем дело в теории информации, представляет собой совокупность сведений о некоторой физической системе. Например, на вход автоматизированной системы управления производственным цехом может быть передано сообщение о нормальном или повышенном проценте брака, о химическом составе сырья или температуре в печи.

Очевидно, если бы состояние физической системы было известно заранее, не было бы смысла передавать сообщение.

В качестве объекта, о котором передается информация, мы будем рассматривать некоторую физическую систему X , которая случайным образом может оказаться в том или ином состоянии, т.е. систему, которой заведомо присуща какая-то степень неопределенности. Очевидно, сведения,

полученные о системе, будут тем ценнее о содержательнее, чем больше была неопределенность системы до получения этих сведений. Возникает вопрос: что значит “большая” или “меньшая” степень неопределенности и чем можно ее измерить.

Степень неопределенности физической системы определяется не только числом ее возможных состояний, но и вероятностями состояний.

Рассмотрим некоторую систему X , которая может принимать конечное множество состояний: x1, x2 ,..., xn с вероятностями P1, P2 ,..., Pn , где

Pi P( X xi )

(14.1)

–вероятность того, что система X примет состояние xi .

Вкачестве меры неопределенности системы в теории информации применяется специальная характеристика, называемая энтропией. Понятие об энтропии является в теории информации основным.

Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифм этих вероятностей, взятая с обратным знаком:

H ( X ) Pi log2 Pi . (14.2)

i 1

Энтропия H (X ) обладает рядом свойств, оправдывающих ее выбор

H ( X ) n 1	log2 1 log2 1 log2 n .
n	n	(14.3)
	H (X ) log2 n,
в качестве характеристики степени неопределенности. Во-первых, она об-
ращается в нуль, когда одно из состояний системы достоверно, а другие –

невозможны. Во-вторых, при заданном числе состояний она обращается в максимум, когда эти состояния равновероятны, а при увеличении числа состояний – увеличивается.

Измерим энтропию системы X , которая имеет n равновероятностных состояний:

xi	x1	x2	….	x
				n
Pi	1	1	….	1
	n	n		n

Имеем:

или

т.е. энтропия системы с равновозможными состояниями равна логарифму числа состояний.

Вычисление энтропии по формуле (14.2) можно несколько упростить, если ввести в рассмотрение специальную функцию:

(P) Plog2 P.	(14.4)
Формула (14.2) принимает вид:
n
H ( X ) (Pi ).	(14.5)

i 1

Рассмотрим совместную энтропию статистически независимых источников сообщений. Пусть имеется два статистически независимых источника X и Y , причем множество состояний x1 ,.., xn принадлежит источ-

нику X , а y1,.., ym – источнику Y . При этом:

n	m
P(xi ) 1;	P( y j ) 1.
i 1	j 1
Если источники X и Y статистически не связаны между собой, то:
P X xi ,Y y j P(xi , y j ) P(xi )P( y j ).		(14.6)

Используя (14.2) и (14.3) для энтропии H (X ,Y ) системы с состояниями (xi , y j ), получим выражение:

H(X,Y) P(xi , yj )log2 P(xi , yj )
i	j
P(xi )P(yj )[log2 P(xi ) log2 P(yj )]
i	j
P(xi )log2		P(xi ) P(yj )log2 P(yj ) H(X) H(Y).
i		j

Следовательно, совместная энтропия статистически независимых источников равна сумме энтропий этих источников. Этот вывод распространяется и на большее число статистически независимых источников.

Рассмотрим условную энтропию статистически зависимых источников сообщений. Пусть имеется два статистически зависимых источника сообщений X и Y . Если источники X и Y коррелированны, то это означает, что между сигналами источников xi , y j существует взаимосвязь, при

которой любому значению, например xi , соответствует значения сигналов источника Y с условными вероятностями:

P( y1 / xi );...; P( y j / xi );...; P( ym / xi ).

Совокупность условных вероятностей для конкретного значения xi позволяет определить частную условную энтропию:

m	P( y j / xi ),
H (Y / xi ) P( y j / xi )log2	P( y j / xi ),
j 1

которая характеризует информационные свойства источника Y после того как стало известно значение xi .

Усредняя частные условные энтропии по всем значениям xi получаем общую условную энтропию источника Y относительно источника X :

n	n m	P( y j / xi ). (14.7)
H (Y / X ) P(xi )H (Y / xi ) P(xi )P( y j / xi ) log2		P( y j / xi ). (14.7)
i 1	i 1 j 1

Так как для статистически зависимых сигналов:

P(xi , y j ) P(xi )P( y j / xi ),

то

n m	P( y j / xi ).
H (Y / X ) P(xi , y j ) log2	P( y j / xi ).
i 1 j 1

Величина H (Y / X ) показывает, какой энтропией в среднем обладает

источник Y , если известен источник X .

Рассмотрим зависимость величины условной энтропии от степени взаимосвязи между источниками X и Y .

Если статистическая связь между сигналами источников X и Y отсутствует, то, сопоставляя равенство (14.6) с выражением

P(xi , y j ) P(xi )P( y j / xi ), получим:

P( y j ) P( y j / xi ).

Подставляя равенства (14.6) и (14.8) в выражение энтропии, найдем:

n m	P(xi )P(yj )log2	n	m
H(Y / X)	P(xi )P(yj )log2	P(yj ) P(xi ) P(yj
i 1 j 1		i 1	j 1

так как

P(xi ) 1.

i 1

Таким образом, в рассматриваемом случае:

H (Y / X ) H (Y ),

(14.8) (14.7) для условной

)log2 P(y j ) H(Y),

т.е. при отсутствии статистической связи между источниками X и Y условная энтропия источника Y относительно источника X равна безусловной энтропии источника Y . Это означает, что всякая информация сигналов y j является новой по отношению к сигналам xi .

При наличии “жесткой” статистической связи между источниками X и Y возможны только два случая: P( y j / xi ) 0 или P( y j / xi ) 1. Так

как при суммировании по j все слагаемые P( y j / xi ) log2 P( y j / xi ) в выражении для H (Y / X ) превращаются в нуль, то и H (Y / X ) 0, т.е. при

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в папке книги

#
12.11.20235.24 Mб6Теоретическая механика и её приложения к решению задач биомеханики..pdf
#
12.11.202314.93 Mб3Теоретическая механика. Сопротивление материалов.pdf
#
20.11.20232.25 Mб15Теоретическая механика.-1.pdf
#
12.11.2023784.25 Кб6Теоретическая механика..pdf
#
12.11.20236.86 Mб3Теоретические и методологические положения процесса управления предприятиями энергетики в условиях модернизации экономики..pdf
#
20.11.2023696.22 Кб10Теоретические основы автоматизированного управления.-1.pdf
#
13.11.202324.2 Mб43Теоретические основы автоматизированного управления..pdf
#
12.11.20231.52 Mб0Теоретические основы безопасности производственной деятельности..pdf
#
12.11.202321.7 Mб15Теоретические основы переработки полимеров (механика процессов)..pdf
#
19.11.202332.46 Mб35Теоретические основы переработки полимеров..pdf
#
12.11.20231.7 Mб24Теоретические основы поиска и разведки месторождений нефти и газа..pdf