книги / Оптимальное проектирование конструкций.-1

ляют недопустимую точку при любом ρ < ∞ и совпадают с точным решением при ρ ∞ , т.е. имеем метод внешней точки.

При 5 − 2x1* ≥ 0 (допустимая область) алгоритм не работает.

Логарифмический штраф

Знак плюс выводит точку за пределы допустимой области, поэтому решение поставленной задачи имеет вид

101

х1* = 13 − 169 − 8(20 − ρ / 2) . 4

Подсчитаем значения параметров решения в зависимости от ρ:

Явно прослеживается существенная зависимость результатов от ρ. Решение стремится к точному при ρ → 0 , однако при таком малом значении задача становится плохо обусловленной и точность методов безусловной оптимизации резко падает.

Таким образом, используя штрафные функции, можно методами безусловной минимизации построить последовательность значений, сходящихся к точкам, оптимальным для задач с ограничениями. При этом необходимо учитывать три момента:

1)решение вопроса о «начале и конце» процесса построения минимизирующей последовательности;

2)учет достоинств и недостатков различных методов штрафных функций;

3)преодоление трудностей безусловной минимизации.

Выше было указано, что результат решения задачи минимизации штрафной функции существенно зависит от параметра ρ. На практике обычно начинают со штрафа умеренной величины, а затем его постепенно увеличивают (или уменьшают) в зависимости от вида штрафа, строя по-

следовательность оптимальных решений х0 , х1, ..., хk . При этом необхо-

димо иметь в виду, что остановка или зацикливание алгоритма может произойти вследствие того, что используемый метод безусловной оптимизации не позволяет найти решение очередной задачи.

Для того чтобы использовать оптимальный вид штрафа, следует учесть достоинства и недостатки метода. Например, метод внешней точки обладает тем преимуществом, что в качестве начального приближения можно выбрать любую точку вне области и решать можно задачи с ограничениями как в форме равенств, так и неравенств. Кроме того, если ка- кие-то ограничения выполняются, то они не входят в штрафную функцию и процесс расчета упрощается. Однако при этом штрафная функция обычно дифференцируема небольшое число раз, что неблагоприятно сказывается на скорости сходимости. Если движение начинается из внутренней точки, то процесс вычислений становится неуправляемым. И, наконец, на каждом итерационном шаге мы получаем в той или иной мере недопустимые решения.

102

Методы внутренней точки порождают последовательность только допустимых точек и имеют обычно производные высоких порядков, что обеспечивает хорошее управление вычислительным процессом. Однако начальная точка всегда должна быть из допустимой области. Кроме того, если используется штраф в виде логарифмической или обратной функции, то при вычислении градиента вклад этих функций никогда не равен нулю, а сами функции при подходе к границе терпят разрыв, что усложняет счет. Наилучшие результаты дает комбинация этих методов.

Наконец, используемые методы безусловной минимизации обычно требуют на каждом шаге определенного числа итераций, поэтому в соответствии с циклом по параметру ρ необходимо учитывать скорость сходимости алгоритма безусловной оптимизации. А если штрафная функция имеет свои особенности, как, например, многие барьерные функции, то использование стандартных процедур становится неэффективным.

Итак, ухудшение обусловленности вспомогательных подзадач в обычных методах штрафных функций существенно ограничивает практическую применимость метода. Поэтому были предложены непараметрические схемы метода штрафных функций, явившиеся попыткой хотя бы отчасти поправить положение, например, такие, как метод центров (Хьюарда) [16], предусматривающий пересчет параметра сразу в штрафную функцию.

Метод Лагранжа. Идея метода рассматривалась ранее (4.8), поэтому сейчас отметим, что методы, основанные на использовании функции Лагранжа, можно отнести к категории параметрических методов штрафных функций, так как для них характерно, что функции-ограничения вводятся в

структуру модифицированной целевой функции совместно с некоторым переменным параметром – множителем Лагранжа.

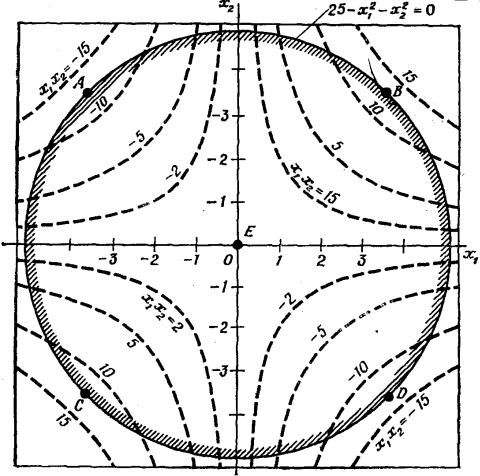
Пример 4.14. Минимизировать функцию f (x) = x1x2 при ограниче-

Перейдем от ограничения-неравенства к ограничению-равенству путем введения новой неотрицательной переменной y2 . Тогда функция Лагранжа примет вид

L(x, ρ ) = x1x2 + ρ (25 − x12 − x22 − y2 ) .

Необходимые условия оптимальности:

103

Из последнего уравнения следует, что возможны два варианта решения: 1) ρ = 0, тогда х1 = х2 = 0 и у = 5, что определяет седловую точку

(рис. 4.28);

точках В и С.

Метод Лагранжа может оказаться непригодным в случае невыпуклых задач и мало эффективен в случае задач большой размерности, поскольку системы уравнений стационарности обычно нелинейны.

Метод множителей. Как уже было показано, широко используемые при оптимизации методы штрафных функций обладают одним существенным изъяном: при увеличении параметра штрафа (что неизбежно в случае,

104

если решение необходимо получить с достаточной степенью точности) вычислительная сложность задачи безусловной оптимизации штрафной функции возрастает. Известны, кроме того, вычислительные трудности реализации метода Лагранжа, основанные на оптимизации расширенной функции Лагранжа. Метод множителей [6] можно рассматривать как комплекс упомянутых выше вычислительных схем. В основе метода множителей лежит конструкция, называемая модифицированной функцией Лагранжа, которая, говоря несколько упрощенно, представляет собой сумму обычной функции Лагранжа и штрафа за нарушение ограничений. Каждая итерация метода множителей заключается в проведении безусловной оптимизации функции Лагранжа по переменным прямой задачи после того, как будут зафиксированы вектор множителей Лагранжа и параметр штрафа. Результат оптимизации используется для перерасчета множителей и, возможно, параметра штрафа. Если на всех итерациях параметр штрафа положить равным нулю, то метод множителей переходит в традиционный метод Лагранжа. Если же вектор множителей Лагранжа считать нулевым, то получим традиционный метод штрафных функций. Важно подчеркнуть, что для сходимости метода множителей нет необходимости неограниченно увеличивать параметр штрафа. Проиллюстрируем суть метода на простом примере.

с= 0, то функцию Лагранжа.

Вотличие от традиционных методов в методе множителей параметр

105

Решая систему, получаем

Анализ показывает, что методом множителей искомую точку минимума удается найти за меньшее число итераций (т.е. с помощью решения меньшего числа вспомогательных задач безусловной минимизации). В обоих методах требуемое число итераций тем меньше, чем с большей скоростью увеличивается параметр штрафа. На практике большое значение

имеет выбор начального приближения для ρ 0 и последовательности ck значений параметра штрафа.

4.3.2.Методы линеаризации

Вряде случаев переход с помощью каких-либо преобразований к задаче минимума без ограничений или с простыми ограничениями существенно помогает поиску решений.

Рассмотрим основанный на линеаризации подход, который позволяет свести общую нелинейную задачу (4.1)–(4.3) либо к последовательности задач линейного программирования, либо к задаче с линейными ограничениями.

Все методы данного класса основаны на разложении нелинейной функции в ряд Тейлора:

106

если отбросить члены второго порядка малости.

Такую функцию можно трактовать как линейную относительно х. Точка х0 называется точкой линеаризации. Следует отметить, что линеаризацию следует использовать с большой осторожностью, так как зачастую она дает грубое приближение.

Все методы, использующие линеаризацию, можно подразделить на три группы:

1)непосредственно использующие последовательность задач линейного программирования;

2)решающие задачи сепарабельного программирования;

3)специально разработанные методы решения задач с линейными ограничениями.

Непосредственное использование последовательности задач линей-

ного программирования. Наиболее простым способом линеаризации является замена общей нелинейной задачи (4.1–4.3) задачей, получаемой при помощи линеаризации всех функций, фигурирующих в исходной задаче.

Линеаризовав все функции в окрестности некоторой точки xi , приведем исходную задачу к следующей: найти минимум функции

Получили задачу линейного программирования, решая которую най-

дем следующую точку xi +1 . Затем проводим линеаризацию в окрестности заданной точки, т.е. строим итерационный процесс. Однако в некоторых случаях процесс может расходиться. Рассмотрим особенности метода на примере.

Пример 4.16 [16]. Минимизировать f (x) = x12 + x22 при ограничениях

g(x) = x12 − x2 ≥ 0;

h (x) = 2 − x1 − x22 = 0;

5 / 2 ≥ x1 ≥ 1/ 2; 3 ≥ x2 ≥ 0.

107

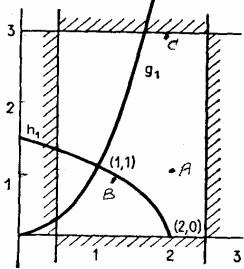
Допустимая область (рис. 4.29) состоит из множества точек кривой от точки (2; 0) до точки (1; 1). Решение легко найти, например, графическим

методом, т.е. х* = (1; 1).

ния нарушены, но уже в меньшей степени, да и значение минимизируемой функции уменьшилось. Линеаризовав задачу в окрестности точки х1 , получим точку x2 = (1,0187; 0,9965). Если сделать еще два приближения, то

получим хорошее приближение к решению исходной нелинейной задачи. Хорошая сходимость, получаемая в этом примере, характерна для задач, функции которых являются умеренно нелинейными. Она теряется

при более ярко выраженной нелинейности.

Для примера рассмотрим ту же задачу, но линеаризацию начнем с

108

g(x0 ) = 3,9995 > 0, h(x0 ) = 0,0. Решение линеаризованной задачи дает точку С (см. рис. 4.29) с координатами x1 = (1,9401; 3). Линеаризованное

значение функции в найденной точке ~( 1) = 3,8203 < ( 0 ); значения ис- f x f x

ходных нелинейных функций: f (x1) =12,764 > f (x0 ), g(x1) = 0,764 > 0,

h(x1) = −8,94 ≠ 0 . Полученные результаты свидетельствуют о расходимо-

сти процесса.

Из рассмотренного примера видно, что линеаризация не гарантирует в общем случае сходимость алгоритма. Чтобы добиться сходимости, налагают ограничения на возможное изменение переменных

− δ j ≤ xij − xij+1 ≤ δ j ,

где δ j – подобранный параметр шага (выбирается из условия, чтобы f (x)

и невязки ограничений уменьшались. Однако это резко уменьшает скорость сходимости.

ние x1 = (1,9899; 0,51); значения исходных нелинейных функций:

f (x1) = 4,2198, g(x1) = 3,45 > 0, h(x1) = −0,25 ≠ 0 . Это лучше, чем до вве-

дения дополнительных ограничений, но хуже, чем в начальной точке. Можно показать, что для лучшей сходимости процесса следует положить

δ 1 = δ 2 = 0,05.

Таким образом, метод непосредственной линеаризации приводит к необходимости решения последовательности задач линейного программирования и может быть использован для решения задач с умеренной степенью нелинейности.

Другим методом линеаризации является так называемое сепарабельное программирование, в основе которого лежит то обстоятельство, что в качестве хорошего приближения нелинейной функции на большом отрезке является ее кусочно-линейная аппроксимация. Для этого весь отрезок разбивается на интервалы и строится линейное приближение на каждом из таких интервалов. Если функция зависит от одной переменной, то путем введения новых переменных можно выразить значение параметра оптимизации и функции на любом отрезке через значения узлов. Если функция зависит от нескольких переменных, то метод применим только к так называемым сепарабельным функциям, представляющим собой сумму функций, каждая из которых зависит только от одной переменной.

109

Однако вместо того, чтобы определить очередное приближение с помощью линеаризации, лучше линейную аппроксимацию использовать только для выявления подходящего направления поиска в каждой точке. В этом случае точку оптимума вдоль данного направления можно определить, проверив значения исходной целевой функции и функций, входящих в ограничения, без помощи линеаризованных ограничений.

Оптимизация при наличии линейных ограничений-равенств. Рас-

Известно, что многие алгоритмы опираются на известные условия оптимальности и наиболее эффективные из них работают по итерационному принципу получения допустимых точек с монотонно убывающим значением целевой функции. Практичность их обусловлена простотой описания возможных направлений для рассматриваемого класса задач.

Определим, какому условию удовлетворяет допустимое направление

поставленной задачи. Для этого возьмем две допустимые точки ~х и х, тогда согласно (4.27), если записать соотношения в матричном виде, будем

всем строкам матрицы а, является допустимым. Отсюда можно предложить следующий алгоритм оптимизации:

1)выбор допустимой точки из условия ax = b;

2)построение допустимого направления из условия ap = 0;

3)переход к следующей точке согласно рекуррентному соотноше-

нию

xk +1 = xk + α k pk ,

где α k – длина шага, определяемая из условия f (xk +1) < f (xk ) .

Рассмотрим один из наиболее популярных методов оптимизации – метод проекций градиента на примере частного случая двумерной задачи с одним ограничением-равенством.

Найти минимум функции f (x1, x2 ) при условиях

ортогонален к линии ограничений.

110