
- •Предисловие
- •1.2. Методы эмпирических и теоретических исследований
- •1.3. Анализ и синтез – основные методы создания новых технических объектов
- •1.4. Элементы теории и методологии научно-технического творчества
- •2. Методы обработки экспериментальных данных
- •2.1. Графическое представление экспериментальных данных
- •3. Численные методы решения уравнений
- •4. Математическое моделирование
- •4.1. Общие принципы математического моделирования
- •4.2. Генерация и преобразование случайных чисел
- •4.3. Примеры моделирования с использованием случайных чисел
- •4.4. Метод статистических испытаний
- •Литература
- •Предметный указатель
Аналогия – один из методов научного познания, посредством которого достигается знание о предметах и явлениях на основании того, что они имеют сходство с другими. Степень достоверности умозаключений по аналогии зависит от количества сходных признаков у сравниваемых явлений, чем их больше, тем большую вероятность имеет заключение. Например, для объяснения электрических явлений, в частности явления резонанса, часто применяется "электромеханическая" аналогия.
Аналогия тесно связана с моделированием или модельным экспериментом.
Если обычный экспериментатор непосредственно взаимодействует с объектом исследований, то в моделировании такого взаимодействия нет, т.к. эксперимент производится не с самим объектом, а с его заменителем.
При исследовании сложных систем с многообразными связями, характеризуемыми как непрерывностью и детерминированностью, так и дискретностью и случайностью, используют системные методы: исследование операций, теорию массового обслуживания, теорию управления, теорию множеств, теорию игр и статистических решений и другие.
В основе системного анализа лежит понятие системы, под которой понимается множество объектов, обладающих заранее определенными свойствами с фиксированными отношениями между ними. На базе этого понятия производится учет связей, используются количественные сравнения всех альтернатив для того, чтобы сознательно выбрать наилучшее решение, оцениваемое каким-либо критерием (например, эффективностью, надежностью, помехоустойчивостью и т.д.).
1.3. Анализ и синтез – основные методы создания новых технических объектов
Создание новых технических объектов (проектирование), необходимость которых определяется потребностями жизнедеятельности человека, можно рассматривать как вид научных исследований, определяемый термином прикладные научные исследования (в отличие от фундаментальных). В данном разделе будет рассмотрена обобщенная структура процесса проектирования, ключевыми элементами которой являются использование методов анализа и синтеза.
Задача проектирования обычно формулируется в виде технического задания, в котором определяются назначение и показатели качества ПК i , i = 1,m объекта проектирования. Например, для термометра показателями качества являются ошибка измерения температуры, диапазон измерения, время установления показаний и, возможно, стоимость; для полосового усилителя – амплитудно- и фазочастотная характеристики; при проектировании системы мобильной связи – зона действия, максимальное число абонентов, габариты и вес мобильного телефона, стоимость услуг. Выполнение требований технического задания можно рассматривать как предмет научного исследования.
Проектирование может осуществляться на разных уровнях: уровень структурной схемы;
уровень принципиальной (электрической) схемы; конструкторско-технологический уровень; уровень изготовления технической документации.
Первым шагом при проектировании является выбор варианта структурной схемы технического объекта, который осуществляется на основании знаний и опыта разработчика, анализа научной литературы и патентной информации по аналогичным объектам. Структурная схема представляет собой набор элементов и их связи. Например, структурная схема радиоприемника включает антенну, антенно-фидерный тракт, предварительный усилитель, смеситель, усилитель промежуточной частоты, детектор, другие элементы и их связи. На уровне проектирования электрических схем элементами являются резисторы, конденсаторы, катушки индуктивности, диоды, транзисторы и их электрические соединения. Этот этап проектирования называется структурным синтезом.
Каждый элемент структурной схемы характеризуется одним или несколькими техническими параметрами. Например, параметры предварительного усилителя – коэффициент усиления и полоса усиливаемых частот; параметры электрической схемы – значения сопротивлений R, емкостей C, индуктивностей L, или, при более подробном рассмотрении – температурные зависимости R, C, L.
На следующем этапе проектирования осуществляется анализ структурной схемы. Цель анализа – определение зависимости показателей качества ПК i технического объекта от параметров его элементов aj , j = 1,n в виде аналитической функции:
ПК i = F (a1 , a2 , …, an ). (1.1)
Выражение (1.1) можно рассматривать как систему уравнений относительно параметров aj , j = 1,n при известных из технического задания значениях показателей качества ПК i . В процессе решения этой системы определяется набор параметров элементов структурной схемы, обеспечивающий выполнение требований технического задания. Этот этап проектирования называется параметрическим синтезом.
Вчастном случае, когда техническое задание сформулировано в виде требования обеспечить максимум или минимум того или иного показателя качества, задача параметрического синтеза переходит в задачу параметрической оптимизации. Для ее аналитического решения можно
вычислить частные производные от выражения (1.1) по параметрам aj , приравнять эти частные производные нулю и решить получившуюся систему уравнений.
Вбольшинстве случаев аналитическое решение задач параметрического синтеза и оптимизации слишком сложно или в принципе невозможно. Тогда можно применять численные методы решения указанных задач на ЭВМ. Однако, поскольку эти методы также довольно сложны с алгоритмической точки зрения и все равно связаны с применением ЭВМ, часто используется принципиально другой подход к решению задач параметрического синтеза и оптимизации.
Этот подход, называемый многовариантным анализом, представляет собой последовательный перебор на ЭВМ всех возможных комбинаций значений параметров {aj}k , k = 1, n! и расчет по формуле (1.1) показателей качества. Расчет повторяется до тех пор, пока при очередной попытке не окажется, что показатели качества удовлетворяют техническому заданию. Комбинация значений параметров {aj}k, при которой достигнут этот результат, и есть искомый набор параметров структурной схемы.
В этом случае процесс проектирования нового технического объекта можно считать завершенным, поскольку определены структурная схема и параметры каждого ее элемента, обеспечивающие выполнение требований технического задания.
Однако, такой благоприятный исход параметрического синтеза (оптимизации) может и не наступить в том случае, когда уравнение (1.1) не имеет решения относительно параметров aj (независимо от способа поиска этого решения – аналитически, численно или методом многовариантного анализа). Это означает, что в рамках выбранной структурной схемы реализация технического объекта с требуемыми показателями качества невозможна и следует вернуться к этапу структурного синтеза.
Рассмотрим ход процесса проектирования на примерах, отмечая использование тех или иных методов исследования.
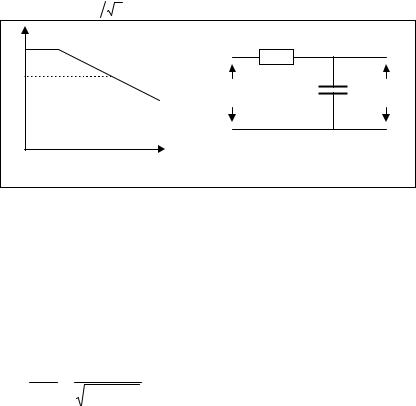
Пример 1.1. Пусть требуется создать фильтр нижних частот с частотой среза ω1 = 2 π f1 , f1 = 3 кГц. Это означает: при ω → 0 модуль комплексного коэффициента передачи фильтра К→1; при ω → ∞ – К→ 0; а на частоте ω1 –
К(ω =ω1) =1 |
2 |
≈0,71. |
|
|
K |
|
|
|
|
1,0 |
|
|
R |
|
0,71 |
|
U вх |
С |
U вых |
|
|
|||
0 |
ω1 |
ω |
Рис.1.4 |
|
Рис.1.3 |
|
|
||
На рис.1.3 качественно изображена амплитудно-частотная характеристика такого фильтра. В данном случае модуль комплексного коэффициент передачи фильтра К и есть показатель качества устройства.
На основании имеющихся знаний в области электротехники выберем электрическую схему устройства (структурный синтез), показанную на рис.1.4.
В результате анализа схемы, который в виду простоты не приводится, получим аналитическую зависимость К=F(ω,τ)
K =U вых = |
1 |
, |
(1.2) |
U вх |
1+ω2τ 2 |
|
|
где τ = RC – постоянная времени фильтра является его единственным
параметром.
Перейдем к параметрическому синтезу фильтра с требуемым коэффициентом передачи. Для этого подставим в (1.2) условие К(ω =ω1) =1  2 и решим получившееся уравнение относительно постоянной времени.
2 и решим получившееся уравнение относительно постоянной времени.
Получим τ = 1/ω1 ≈ 53 мкс.
Процесс проектирования завершен, поскольку выбраны схема фильтра и его параметры, обеспечивающие выполнение технического задания.
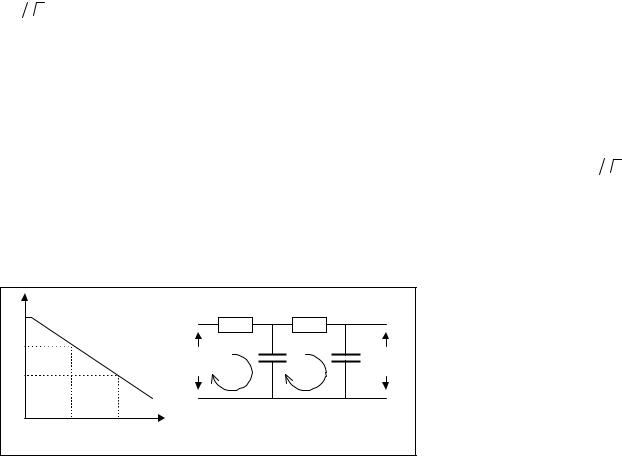
В качестве следующего примера рассмотрим более сложное техническое задание на проектирование фильтра нижних частот. Теперь требуется обеспечить не только частоту среза ω1 = 2 π f1 , f1 = 3 кГц, но и крутизну спада частотной характеристики, определяемую условием К (ω2 = 2ω1) ≤ 1  6
6
≈ 0,41, причем желательно обеспечить минимум величины К на частоте ω2 в рамках выбранной электрической схемы.
В данном случае показателями качества устройства являются два значения модуля комплексного коэффициент передачи фильтра на частотах ω1 и ω2
(рис.1.5).
1,0 |
K |
|
R1 |
|
R2 |
|
|
|
|
|
|||
0,71 |
|
|
U вх |
C1 |
С2 |
U вых |
|
|
|
||||
0,41 |
|
|
I1 |
|
I2 |
|
0 |
ω1 |
ω2 |
ω |
|
Рис.1.6 |
|
|
Рис.1.5 |
|
|
|
|
Выберем для начала электрическую схему устройства (структурный синтез) такую же, как и в предыдущем примере (рис.1.4). Повторив процедуру анализа и параметрического синтеза фильтра, получим значение параметра τ = 1/ω1 , обеспечивающее значение К ≈ 0,71 на частоте ω1 Далее, проверим, выполняется ли требование К ≤ 0,41 на частоте ω2 . Для
этого подставим в (1.2) τ = 1/ω1 и ω = ω2 = 2ω1. Получим К ≈ 0,45, то есть в рамках выбранной электрической схемы одно из требований технического задания не может быть выполнено. Следовательно, необходимо вернуться к
структурному синтезу.
Выберем более сложную схему фильтра, состоящую из двух звеньев (рис.1.6). На первый взгляд, можно предположить, что амплитудно-частотная характеристика такого фильтра представляет собой произведение характеристик его звеньев. Так ли это на самом деле?
При анализе схемы воспользуемся одним из частных методов исследования – методом контурных токов. В соответствии с выбранными положительными направлениями токов, показанными на рис.1.6, получим следующую систему уравнений
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
+ |
|
|
|
− I |
2 |
|
|
=Uвх |
|
|
|
|||||
I1 R1 |
|
|
jωC2 |
|
|
|
||||||||||||
|
|
|
|
jωC |
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
= 0 , |
||
− I |
|
|
C |
+ |
I |
|
R |
|
+ |
|
+ |
|
|
|||||
1 jω |
|
|
jωC |
jωC |
|
|||||||||||||
|
|
|
|
2 |
2 |
|
|
2 |
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|

которую преобразуем к виду
I |
(1+ jω |
R C |
)−I |
|
= jωC U |
|
|
|
||||||
1 |
|
|
|
|
1 1 |
|
|
2 |
|
1 вх |
|
|
||
− I |
|
C2 |
|
+ I |
|
1 |
+ |
|
C2 |
+ jωR |
C |
|
= 0 . |
|
|
C |
|
C |
|||||||||||
|
|
1 |
|
|
2 |
|
|
|
2 |
|
2 |
|
||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
Действуя стандартными алгебраическими методами, получим уравнение с одним неизвестным I2, решение которого
I 2 |
= |
|
|
|
jωC2U вх |
|
|
|
|
|
|
|
. |
|
||||
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
C2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ C |
|
|
− C |
|
|||||||||||
|
|
|
(1+ jωR1C1 ) 1 |
+ jωR2C2 |
|
|||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|||
С учетом соотношения U |
вых |
= |
|
I2 |
окончательно получим |
|||||||||||||
|
jωC2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
K |
= |
|
|
|
1 |
|
|
|
|
|
|
|
|
. |
|
(1.3) |
||
|
|
|
|
C2 |
|
|
|
|
C2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|||||
|
|
(1+ jωR1C1 ) 1 |
+ C + jωR2C2 |
|
|
|
|
|||||||||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|||||
Только при выполнении условия C2 << C1, которое обеспечивает полную передачу напряжения от первого звена фильтра ко второму, формула (1.3) упрощается и приобретает вид произведения характеристик звеньев фильтра
K = |
|
1 |
1 |
, |
(1.4) |
|
1 +ω2τ12 |
1 +ω2τ22 |
|
|
|
где |
τ1 |
и |
τ2 – |
постоянные |
времени звеньев фильтра являются его |
параметрами.
Перейдем к параметрическому синтезу фильтра с требуемыми значениями
коэффициента |
|
|
передачи |
К=1 2 |
и |
||||
К ≤ 1 |
6 соответственно на частотах ω1 |
и ω2 = 2ω1. При подстановке этих |
|||||||
значений в (1.4) получим систему уравнений |
|
||||||||
1 |
= |
1 |
2 |
2 |
1 2 |
2 |
|
|
|
2 |
|
1 +ω1 τ |
1 |
1 +ω1 |
τ2 |
(1.5) |
|
|
|
1 |
≥ |
1 |
|
|
1 |
, |
|
|
|
6 |
|
1+ω22τ12 |
1+ω22τ22 |
|
|
|
|||
которую, введя обозначения x=(ω1τ1) 2 > 0 и y=(ω1τ2)2 > 0, преобразуем к виду
2 = (1+ x)(1 + y) |
|
6 ≤ (1+ 4x) (1+ 4 y) . |
(1.6) |
Решим систему (1.6) методом подстановки. Из первого уравнения найдем
x = |
|
1 |
− y |
, |
(1.7) |
|
1 |
+ y |
|||||
|
|
|
||||
и подставим во второе неравенство. Из (1.7) следует, что область определения неизвестных: y<1 и x<1. После преобразований получим квадратное неравенство вида
12y2 −11y +1 ≤ 0 ,
которое с учетом области определения y выполняется при одном из условий
0 < y < 0,10 или 0,81 < y < 1.
