Интерполяционный ряд Котельникова-Шеннона

Спектр дискретного сигнала представляет собой сумму сдвинутых копий спектров аналогового сигнала с шагом сдвига, равным частоте дискретизации. Если спектры не перекрываются, то по центральной копии можно точно восстановить исходный сигнал. Покажем это. Имеем фуры обратной дискретной функции:

Умножим на :

Получим непрерывный спектр в пределах, равный в пределах главного частотного диапазона.

Обратное преобразование Ф такого спектра должно давать конечный и непрерывный сигнал: имеем произведение функций.

Заметим, что:

Тогда:

Следовательно, получен интерполяционный ряд Котельникова-Шеннона. Из формулы следует, что если наибольшая частота в спектре аналогового сигнала не превышает частоты его дискретизации, то он без потери точности может быть восстановлен посредством ряда Котельникова-Шеннона.

По сути, система образует ортогональный базис пространства . Ряд числовых значений интегрального синуса для дискретных значений при суммировании по дает гребневую функцию.

Однако, в отличие от , в интервалах между отсчетами, имеет не нулевые, а осциллирующие значения, суперпозиция которых дает восстановленное значение сигнала.

Запись ряда Котельникова-Шеннона относительно , где спектр сигнала :

Другие записи ряда К-Ф:

Представление рядом Котельникова-Шеннона является частным случаем разложения

где роль выполняют отсчеты , а функции отсчетов:

Вывод: Сигнал с ограниченным спектром с шириной полосы полностью определяется точками отсчета, отстоящими во времени на интервале:

Если сигнал известен на и спектр , то по ряду Котельникова-Шеннона определить весь сигнал нельзя, хотя в точках отсчета ошибки не будет.

Аналогично, может быть рассмотрена задача дискретизации спектра заданного на финитного сигнала.

При дискретизации спектра с шагом

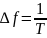
динамические представления сигнала становятся периодическими с периодом . Для восстановленного сигнала (точного) в пределах главного периода частотный шаг должен удовлетворять условию:

Дискретные преобразования сигналов

Дискретное преобразование Ф

Цифровая обработка сигналов оперирует с дискретно преобразованными сигналами и реализует дискретные алгоритмы. Математический аппарат дискретных преобразований подобен преобразованиям аналоговых сигналов, но имеет существенные отличия, не учет которых может приводить к значительным ошибкам.

Дискретное преобразование Ф может быть получено непосредственно из интегральных преобразований Ф заменой интеграла на интегральные суммы.

приводит к периодизации ее спектра.

приводит к периодизации функции времени.

Надо иметь в виду, что

есть дискретизация непрерывного спектра дискретной функции ,

- дискретизация непрерывной функции .

И при восстановлении непрерывных функций и по дискретным значениям (отсчетам) соответствия и гарантированы только при выполнении условий теоремы Котельникова-Шеннона.

Для дискретных преобразований

и функция и ее спектр дискретны и периодичны, а числовые массивы их представления соответствуют заданию на главных периодах (на ) и (на ), где – количество отсчетов, при этом:

Выше приведенные условия являются условиями информационной равноценности динамических и частотных форм представления дискретных сигналов.

Другими словами, число отсчетов функции и спектра функции этой должны быть одинаковыми.

При реализации обработки массивов отсчетов часто принимают , а преобразование Ф выполняют по (номер шага по частоте) на главных периодах.

Для четных :

Для нечетных границы главного периода по частоте ( ) устанавливаются равными 1. и – ДПФ - дискретные преобразования Ф.

В вычислительных операциях на ЭВМ для исключения отрицательных частотных аргументов ( ) и использования идентичных алгоритмов прямого и обратного преобразования Ф, главный период спектра принимается в интервале , т.е. ( ), а суммируется производная от 0 до .

Для ДПФ справедливы все свойства интегральных преобразований Ф, но следует учитывать периодичность дискретных функций и спектров. Так произведению дискретных спектров будет соответствовать свертка периодезированых функций во времени и наоборот. Такая свертка называется циклической.

БПФ. При вычислении ПФ среди множителей (sin и cos) есть много периодически повторяющихся значений. Алгоритм БПФ группирует слагаемые с одинаковыми множителями в пирамидальный алгоритм, что значит уменьшение числа операций.

Пример 2.

Дискретное преобразование Лапласа (ДПЛ)

Дискретное преобразование Лапласа получается из интегрального преобразования путем дискретизации аргументов

где – комплексная частота,

При преобразование Лапласа превращается в односторонне преобразование Ф, а для каузальных сигналов – в полное преобразование Ф.

За счет выбора сигнал всегда можно сделать затухающим, конечным по энергии, что и требуется для существования его Ф-образа.

Z-преобразование сигналов

Z - преобразование сигналов играет для дискретных сигналов ту же роль, что и преобразование Лапласа для непрерывных сигналов.

Смысл:

отсчеты ставится в соответствие степенной полином:

где - произвольная комплексная переменная. – -образ или изображение .

Преобразование имеет смысл для тех значений , для которых ряд сходится, т.е. сума не имеет полюсов и особых точек.

Пример:

Возможна запись , что тоже самое??? пределы . Смысл величины в полиноме в том, что она является оператором сдвига (единичной задержки) по координатам функции.

Умножение Z-образа на означает задержку сигнала на интервалов.

-образы с положительными степенями соответствуют каузальным сигналам. Однако при обработке массива значений сигналов на ЭВМ каузальность не есть ограничение, т.к. возможно использование отрицательных степеней , что будет означать использование будущих значений в массиве.

Примеры Z-преобразований.

Импульсы Кронекера

В нулевой точке ( ) .

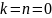Функция Хевисайда (единичный скачок)

Связь Z-преобразований с преобразованиями Ф и Л

Запишем дискретный сигнал в виде:

Определим спектр по теореме запаздывания:

Выполним замену переменных:

тогда:

Т.е. ДПФ есть частный случай Z-преобразования при . Аналогично, подстановкой:

может осуществляться переход к ДП Лапласа. Т.е. имеем пары.

Прямое преобразование:

при

при

Обратное преобразование:

при

при

Свойства Z-преобразований

Все свойства ДПФ действительны для Z-преобразований.

Линейность

Если , то

Задержка на n тактов:

Действительны (для Z-преобразований) все теоремы о свертках.