Стат. обр. 4195-96. 2014 / Конспект лекции 2. Осн. статистика

Лекция 2

ОСНОВНАЯ СТАТИСТИКA

Математическая статистика изучает как отдельные переменные, так и совокупности переменных, устанавливая качественное или количественное соотношение между ними. Обязательным условием применения математических методов статистической обработки данных является случайность этих данных. Какие данные могут подвергаться статистической обработке? Во-первых в интернете имеется большое количество ежегодных статистических справочников, характеризующих состояние регионов РФ и РФ в целом. Во-вторых это могут быть данные по функционированию каких-либо объектов, например, информационных сетей. В третьих результаты имитационного моделирования.

Все эти исходные статистические данные представляют собой распределения случайных чисел. Полностью задать распределение случайной величины можно с помощью функции распределения (ФР), или функции плотности (ФП). Отметим что есть и другие возможности, например, – моментная производящая функция (МПФ).

ФР – это вероятность того, что случайная величина Х не превысит своего текущего значения х.. (2.1)

Наиболее часто используется ФП, как вероятность попадания случайной величины на участок .

(2.2)

(2.3)

Основные статистические законы распределения случайных чисел: равномерный, экспоненциальный и нормальный.

Равномерный закон

Функция распределения и функция плотности равномерного закона приведены на рис.2.3.

Рис.2.3. Функция распределения и функция плотности равномерного закона

Диапазон существования равномерного закона определяется границами a и b, которые являются его параметрами. ФР равномерного закона определяется двумя параметрами: a и b:

_(2.4)

Функция плотности равномерного закона:

_(2.5)

_{Экспоненциальный закон}

ФР экспоненциального закона приведена на рис. 2.4.

Рис.2.4. Функция распределения экспоненциального закона

ФП экспоненциального закона приведена на рис. 2.5.

Рис.2.5. Функция плотности экспоненциального закона

Экспоненциальный закон имеет диапазон своего существования от 0 до ¥. Функция плотности экспоненциального закона:

(2.6)

ФП экспоненциального закона определяется всего одним параметром m. Для потоков событий это количество транзактов (заявок), поступающих за единицу времени, для процессов обслуживания – это количество заявок, которое может быть обслужено при их непрерывном поступлении.

ФР экспоненциального закона можно вычислить по ФП:

(2.7)

Нормальный закон

Нормальный закон имеет диапазон существования от -∞ до +∞. Функция плотности нормального закона определяется двумя параметрам: математическим ожиданием - m₁ и средним квадратическим отклонением – σ:

(2.8)

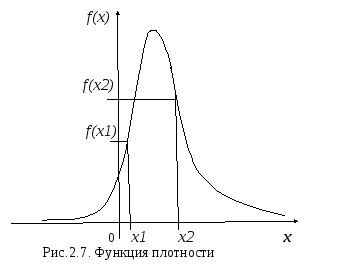
Функция распределения нормального закона приведена на рис.2.6, функция плотности – на рис.2.7.

Основные статистические характеристики распределений

случайных величин

По ФП можно вычислить вероятность, что случайная величина примет значение х_i, для этого требуется вычислить p_i =f( x_i),и вероятность попадания случайной величины в интервал с границами от a до b, для этого требуется вычислить:

(2.9)

ФР и ФП полностью определяют распределение случайной величины. Иногда этого не требуется и тогда ограничиваются вычислением только основных количественных характеристик.

Характеристики положения случайной величины – это начальные и центральные моменты, которые для непрерывных и дискретных законов распределений вычисляются по следующим формулам:

; (2.10)

, (2.11)

где

- математическое ожидание;

s – порядок момента.

Среднее квадратическое отклонение можно вычислить по следующей формуле:

(2.12)

М_о – мода – это значение случайной величины, при котором функция плотности максимальна.

М_е - медиана – это такое значение случайной величины, для которого вероятность появления случайного числа Х меньше медианы, равна вероятности появления случайного числа Х больше медианы:

(2.13)

Медиана делит распределение случайных чисел пополам.

I II

Асимметрия. . (2.14)

Для нормального закона А=0. Распределение I имеет положительную асимметрию; распределение II – отрицательную. Для симметричных распределений асимметрия равна нулю.

Рис.2.8. Асимметрия

Для оценки «островершинности» распределения используется эксцесс.

. (2.15)

Для нормального закона распределения и поэтому эксцесс равен нулю. Чем меньше среднее квадратическое отклонение, тем эксцесс больше и чем больше среднее квадратическое отклонение, тем эксцесс меньше.

Рис.2.9. Эксцесс

Основная статистика, вычисляемая по экспериментальному распределению случайных чисел

По эмпирическому распределению случайных чисел вычисляются:

1. Оценка математического ожидания (среднее)

(2.16)

2. Оценка стандартного отклонения

; (2.17)

(2.18)

3. Коэффициент вариации

. (2.19)

3. Оценка дисперсии:

. (2.20)

Для нормального закона могут быть от до

3. Cтандартная ошибка среднего

. (2.21)

3. Оценка медианы – число, являющееся серединой совокупности случайных чисел, т.е. половина из них меньше медианы, а половина больше P{X<M_e^*}=P(X>M_e^*)

4. Мода. Наиболее часто встречающееся значение. Для нормального закона медиана и мода в идеальном случае совпадают со средним значением.

5. Оценка ассиметрии:

. (2.22)

3. Стандартная ошибка ассиметрии:

. (2.23)

3. Оценка эксцесса:

(2.24)

3. Стандартная ошибка эксцесса:

(2.25)

3. Ошибка вычисления дисперсии:

(2.26)

Проверка нормальности распределения по асимметрии, эксцессу и медиане

Если вычисление значения асимметрии и эксцесса по абсолютной величине меньше двух своих стандартных ошибок соответственно 2· и 2·, то считается, что имеющиеся статистические данные не противоречат гипотезе об их подчинении нормальному закону, в противном случае гипотезу рекомендуется опровергнуть.

a э

-2S_стасс 0 2S_стасс -2S_стэкс 0 2S_стэкс

Рис.2.10 Рис.2.11

Ещё один вид проверки экспериментального распределения на «нормальность» можно провести по разнице между медианой и средним значением которое не должно превышать двух стандартных ошибок среднего:

|m₁^*-M_e^* |≤2·S_ст.

| m₁^* -M_e^*|

-2S_стср 0 2S_стср

Рис.2.12