5.4. Аппроксимация экспериментальных данных нелинейными
зависимостями, сводимыми к линейным заменой переменных
Логарифмическая зависимость
Некоторые сравнительно несложные зависимости можно свести к линейным простой заменой переменных. Например, логарифмическую зависимость:
Y=b lnX. (5.4.1)
Для её линеаризации достаточно принять, что lnX=x Y=y,тогда получим линейную зависимость
y=bx (5.4.2) Для зависимости (5.4.2) получена формула для расчёта коэффициента b :
(5.4.3)
Например, логарифмическую зависимость:
Y=b0+b1 lnX. (5.4.4)
Для её линеаризации достаточно принять, что lnX=x Y=y,тогда получим линейную зависимость
y=b0+b1x (5.4.5) Для зависимости (5.4.5) преобразованием (5.2.21) получены следующие формулы для расчёта коэффициентов b0 и b1:
(5.4.6)
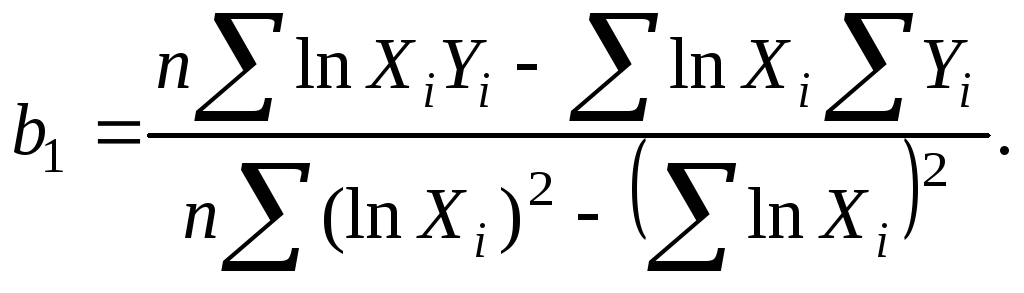(5.4.7)
По (5.4.6) и (5.4.7) находят искомые коэффициенты.
В геометрической интерпретации процесс линеаризации сводится к логарифмическому изменению масштаба оси абсцисс.
y=Y
•
•
•
•
• • • •
•
•
X, x=lnX
Рис.5.4.1
Гиперболическая зависимость
Зависимость
называется гиперболической. Для того,
чтобы для вычисления коэффициентовb0
и
b1
использовать формулы, полученные для
линейной зависимости y=b0+b1x
(5.2.21),
достаточно
произвести замену переменных
и получить формулы для расчёта
коэффициентов гиперболтческой
зависимости:
b0=
.
(5.4.8)
b1=
.
(5.4.9)
По уравнению регрессии проведём прямую линию на рис.5.4.2.
у
(0.1;9.8)
9 •
8
•
7
•
4
•
(0.5;1.8)
1
•
0.1
0.2 0.3 0.4 0.5 х
Рис.5.4.2. Координаты экспериментальных точек и аппроксимиру-
щая
их гиперболическая зависимость
