4.9. Коэффициенты корреляции количественных признаков

В качестве количественной меры оценки взаимосвязи между случайными величинами используются коэффициент линейной корреляции и эмпирическое корреляционное отношение. Оба показателя введены Пирсоном.

Коэффициент линейной корреляции используется в случае нормальности распределений случайных величин х и у и наличия линейной зависимости между ними. Он вычисляется по n экспериментальным данным по следующей формуле:

(4.9.1)

В формуле (4.9.1) оценки математических ожиданий переменных х, у и их произведения вычисляются по формулам:

(4.9.2)

Оценки вторых начальных моментов требуются для вычисления средних квадратических отклонений. Для этого используются следующие формулы:

(4.9.3)

(4.9.4)

Если коэффициент линейной корреляции близок к 1, то корреляционная связь между переменными положительная, близкая к линейной (рис.4.9.1). Если коэффициент линейной корреляции близок к -1, то корреляционная связь между переменными отрицательная, близкая к линейной (рис.4.9.2). Если коэффициент линейной корреляции близок к 0, то между переменными имеется слабая корреляционная связь (рис.4.9.3). Для независимых переменных коэффициент линейной корреляции равен нулю.

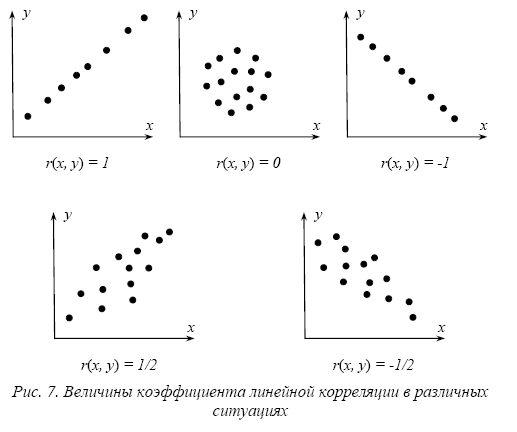
Рис.4.9.1. Графики зависимости между случайными переменными при

различных значениях коэффициента линейной корреляции

Оценить существенность коэффициента линейной корреляции между случайными переменными по критерию Стьюдента можно при условии, что распределения этих случайных величин подчиняется нормальному закону и что они имеют совместное двумерное нормальное распределение.

Коэффициент линейной корреляции является случайной величиной, и поэтому для него может быть вычислена стандартная ошибка

. (4.9.5)

По статистическим таблицам находим критическое значение коэффициента линейной корреляции.

. (4.9.6)

В случае, если значение коэффициента линейной корреляции, вычисленное по (4.9.1), по абсолютной величине не меньше 0,8, то можно ожидать наличие между переменными линейной зависимости и в уравнения регрессии вводить сами факторы в первой степени. Если значение коэффициента линейной корреляции по абсолютной величине лежит в диапазоне от критического значения до 0,8, то в уравнения регрессии рекомендуется вводить сравнительно несложные функции от факторов. Рекомендуется использовать следующие функции от факторов x_i; : для увеличения масштаба факторах относительно результативного показателя эффективности у; - для уменьшения масштаба факторах относительно результативного показателя эффективности у; - для отображения обратной связи между фактором х и результативным показателем эффективности у. Если значение коэффициента линейной корреляции по абсолютному значению меньше критического, то такие факторы рекомендуется не включать в уравнения регрессии.

Эмпирическое корреляционное отношение вычисляется по формуле

(4.9.7)

где δ^* – оценка межгруппового среднего квадратического отклонения;

σ_у^* – оценка среднего квадратического отклонения результативного

признака.

. (4.9.8)

Эмпирический коэффициент детерминации в долях от 1 показывает на сколько изменение результативного признака объясняется изменением факторного признака, Он вычисляется по формуле:

(4.9.9)

Пример 4.9.1

Вычислим коэффициент линейной корреляции и эмпирическое корреля-ционное отношение для оценки тесноты связи между оборотным капиталом предприятий и их прибылью, Статистические данные по указанным признакам для 25 предприятий приведены в таблице 4.9.1.

Таблица 4.9.1. Исходные данные для примера 4.9.1

№ предприятия - i	Оборотный капитал - хi в тыс. руб.	Прибыль - yi в тыс. руб.
1	634	127
2	536	86
3	726	184
4	510	82
5	656	137
6	547	110
7	809	193
8	732	190
9	807	184
10	766	189
11	664	135
12	751	175
13	556	115
14	836	210
15	739	169
16	846	215
17	934	264
18	927	241
19	851	235
20	678	167
21	832	275
22	748	157
23	717	164
24	944	314
25	959	286

Для наглядности вычислений добавим в таблицу 4.9.1 ещё три вспомогательных столбца со значениями: х_i², y_i², x_i y_i и поместим полученные результаты в таблицу 4.9.2.

Таблица 4.9.2. Предварительные расчёты для примера 4.9.1

Номер предпри- ятия - i	Оборотный капитал- хi	Прибыль - yi	xi2	yi2	xi yi
1	634	127	401956	16129	80518
2	536	86	287296	7396	46096
3	726	184	527076	33856	133584
4	510	82	260100	6724	41820
5	656	137	430336	18769	89872
6	547	110	299209	12100	60170
7	809	193	654481	37249	156137
8	732	190	535824	36100	139080
9	807	184	651249	33856	148488
10	766	189	586756	35721	144774
11	664	135	440896	18225	89640
12	751	175	564001	30625	131425
13	556	115	309136	13225	63940
14	836	210	698896	44100	175560
15	739	169	546121	28561	124891
16	846	215	715716	46225	181890
17	934	264	872356	69696	246576
18	927	241	859329	58081	223407
19	851	235	724201	55225	190985
20	678	167	459684	27889	11326
21	832	275	692224	73625	228800
22	748	157	559504	24649	117436
23	717	164	514089	26896	117588
24	944	314	891`136	98596	296416
25	959	286	919681	81796	274274
Итого	18705	4604	14401233	937314	3625593
Оценки моментов	18705/25= =748,2	4604/25= =184,16	14401233/25= =576049,32	937314/25= =37492,56	3625593/25= =145023,72

Вычислим средние квадратические отклонения:

Вычислим коэффициент линейной корреляции.

Вычислим критическое значение коэффициента линейной корреляции:

Значение t_крит=2,0687 находим по статистическим таблицам для

рекомендуемого уровня значимости α=0.05 и количества степеней свободы:

п-2=25-2=23.

Ввиду того, что вычисленное значение коэффициента линейной корреля-

ции превышает критическое значение, то анализируемую связь будем счи-тать существенной, а ввиду того что оно превышает 0,8, то делаем заключе-ние, что эта связь положительная и близкая к линейной.

Для вычисления эмпирического корреляционного отношения сгруппи-

руем предприятия и результаты группировки представим в таблице 4.9.3.

Таблица 4.9.3. Исходные данные для вычисления корреляционного

отношения

Номер интервала - i	Границы интервала	Кол. предпри- ятий - ni	Середина ин- тервала - xi	Средняя прибыль - уi
1	510-600	4	555	98,25
2	600-690	4	645	141,50
3	690-780	7	735	175,43
4	780-870	6	825	218,67
5	879-960	4	915	276,25

Вычислим оценку межгрупповой дисперсии:

=((98,25-184,16)²×4+(141,5-184,16)²×4+

+ (175,43-184,160)²×7+(218,67-184,16)²×6+(276,25-184,16)²×4)/25=3136,12.

Вычислим общую дисперсию результативного признака:

Вычислим эмпирическое корреляционное отношение:

Вычислим эмпирический коэффициент детерминации:

Эмпирический коэффициент детерминации показывает, что более 87% изменения результативного признака объясняется изменением факторного признака, что позволяет сделать заключение о наличии существенной связи между ними.

Возможность применения линейной функции для представления

зависимости y=f(x) можно оценить по величине ω, вычисляемой по формуле:

Ввиду того, что вычисленное значение ω² по абсолютному значению

меньше критического значения критерия Фишера F_крит=3,1, найденного по статистическим таблицам для рекомендуемого значения уровня значимости α=0,05 и двух степенях свободы: k₁₌k-2=5-2=3 и k₂=n-k=25-5=20, то делаем заключение о сильной близкой к линейной связи результативного признака у с факторным признаком х.

Вычислим коэффициенты линейного уравнения регрессии y=b₀+b₁;

Таким образом, получили линейное уравнение:

Вычислим коэффициент эластичности, который показывает на сколько процентов изменится результативный признак при изменении факторного признака на один процент:

Вычислим β-коэффициент, который показывает на сколько процентов изменится среднее квадратическое отклонение результативного признака при изменении среднего квадратического отклонения факториного признакана один процент:

Пример 4.9.2

Провести корреляционный анализ показателей нефтегазодобывающей отрасли России, представленных в таблице 4.9.4.

Таблица 4.9.4. Исходные данные для примера 4.9.2

Показатель	Код	1996 г.	1977 г.	1998 г.	1999 г.	2000 г.	2001 г.	2002 г.
Добыча нефти в млн. тонн	y	269,91	270,94	264,70	268,53	281,29	301,73	341,60
Разведочное бурение в тыс. метрах	x1	1026,4	1006,7	789.0	824,9	1013,7	1145,1	1410,4
Эксплуатацион- ное бурение в тыс. метрах	x2	6762,2	6997,7	4697,7	4872,5	8286,7	9011,0	10024,5
Всего бурение в тыс. метрах	x3	7788,6	8004,4	5486,7	5697,4	9300,4	10156,1	11434,9
Кол. добываю- щих скважин	x4	106645	101224	97557	101937	109939	114883	113672
Кол. простаива- ющих скважин	x5	37396	35958	34131	32932	31940	31479	34228
Всего скважин	x6	144041	137182	131688	134869	141879	146362	147900
Ввод новых скважин	x7	3419	3001	2376	2552	3405	4023	3901
Закуплено бе- тонита в тыс. т.	x8	78,94	86,66	60,25	56,41	70,97	67,32	73,00

По данным таблицы 4.9.4 аналогично предыдущему примеру вычислены коэффициенты линейной корреляции между всеми переменными и результаты вычислений помещены в таблицу 4.9.5.

Таблица 4.9.5. Коэффициенты линейной корреляции для переменных

примера 4.9.2

Коды	y	x1	x2	x3	x4	x5	x6	x7	x8
y	1	0,932	0,850	0,862	0,865	-0,242	0,765	0,758	0,099
x1	0,932	1	0,937	0,948	0,831	-0,015	0,894	0,880	0,426
x2	0,830	0,937	1	0,999	0,916	-0,229	0,911	0,944	0,423
x3	0,862	0,948	0,999	1	0,913	-0,210	0,915	0,944	0,425
x4	0,865	0,831	0,916	0,913	1	-0,399	0,947	0,961	0,157
x5	-0,242	-0,015	-0,299	-0,210	-0,388	1	-0,071	-0,174	0,613
x6	0,765	0,894	0,911	0,915	0,947	-0,071	1	0,979	0,383
x7	0,758	0,882	0,944	0,944	0,961	-0,174	0,979	1	0,391
x8	0,099	0,426	0,423	0,425	0,157	0,613	0,383	0,391	1

Вычислим критическое значение коэффициента линейной корреляции:

Значение t_крит=2,5706 находим по статистическим таблицам для

рекомендуемого уровня значимости α=0.05 и количества степеней свободы:

п-2=7-2=5.

Проведём анализ результатов, приведённых в таблице 4.9.5. Так как коэффициенты линейной корреляции /r_yx5/=0,242<r_крит и /r_yx8/=0,099<r_крит, то связь результативного показателя у с факторами х₅ и х₈ является несущественной и поэтому эти факторы не будем включать в уравнение регрессии. Для решения вопроса о включении в уравнение регрессии других факторов будем последовательно рассматривать имеющиеся факторы попарно.

Сначала проверим выполнение неравенств для результативного показателя у и факторов х₁ и х₂.

r_yx1>r_x1x2; 0,932<0,937; не выполняется.

r_yx2>r_x1x2; 0,850<0,937; не выполняется.

Оба неравенства не выполняются, Это указывает на то, что связь между факторами х₁ и х₂ является более существенной чем между этими факторами и результативным показателем у. В этом случае рекомендуется оставить для включения в уравнение регрессии фактор, у которого коэффициент линейной корреляции больше. Так как r_x1=0,932>r_x2=0,850, то для включения в уравнение регрессии оставляем фактор х₁.

Проверим выполнение неравенств для результативного показателя у и факторов х₁ и х₃.

r_yx1>r_x1x3; 0,932<0,948; не выполняется.

r_yx3>r_x1x3; 0,862<0,948; не выполняется.

Оба неравенства не выполняются. Это указывает на то, что связь между факторами х₁ и х₃ является более существенной чем между этими факторами и результативным показателем у. В этом случае рекомендуется оставить для включения в уравнение регрессии фактор, у которого коэффициент линейной корреляции больше. Так как r_yx1=0,932>r_уx3=0,862, то для включения в уравнение регрессии оставляем фактор х₁.

Проверим выполнение неравенств для результативного показателя у и факторов х₁ и х₄.

r_yx1>r_x1x3; 0,932>0,785; выполняется.

r_yx3>r_x1x3; 0,865>0,785; выполняется.

Оба неравенства выполняются. Это указывает на то, что связь между факторами х₁ и х₃ является менее существенной чем между этими факторами и результативным показателем у. В этом случае рекомендуется оставить для включения в уравнение регрессии оба фактора: х₁ и х₄.

Проверим выполнение неравенств для результативного показателя у и факторов х₁ и х₆.

r_yx1>r_x1x6; 0,932>0,894; выполняется.

r_yx6>r_x1x6; 0,765<0,894; не выполняется.

Первое неравенство выполняется, а второе не выполняется. Это ещё раз подтверждает что связь между фактором х₁ и результативным показателем у является существенной. Не выполнение второго неравенства позволяет не включать фактор х₆ в уравнение регрессии, но для большей убедительности при принятии такого решения проверим выполнение неравенств для результативного показателя у и факторов х₄ и х₆.

r_yx4>r_x4x6; 0,865<0,947; не выполняется.

r_yx6>r_x4x6; 0,765<0,947; не выполняется.

Оба неравенства не выполняются. Это указывает на то, что связь между факторами х₄ и х₆ является более существенной чем между этими факторами и результативным показателем у. В этом случае рекомендуется оставить для включения в уравнение регрессии фактор, у которого коэффициент линейной корреляции больше. Так как r_yx4=0,865>r_уx6=0,765, то для включения в уравнение регрессии оставляем фактор х₄.

Проверим выполнение неравенств для результативного показателя у и факторов х₁ и х₇.

r_yx1>r_x1x7; 0,932>0,882; выполняется.

r_yx7>r_x1x7; 0,758<0,882; не выполняется.

Первое неравенство выполняется, а второе не выполняется. Это ещё раз подтверждает что связь между фактором х₁ и результативным показателем у является существенной. Не выполнение второго неравенства позволяет не включать фактор х₇ в уравнение регрессии, но для большей убедительности при принятии такого решения проверим выполнение неравенств для результативного показателя у и факторов х₄ и х₇.

r_yx4>r_x4x7; 0,865<0,961; не выполняется.

r_yx7>r_x4x7; 0,758<0,961; не выполняется.

Оба неравенства не выполняются. Это указывает на то, что связь между факторами х₄ и х₇ является более существенной чем между этими факторами и результативным показателем у. В этом случае рекомендуется оставить для включения в уравнение регрессии фактор, у которого коэффициент линейной корреляции больше. Так как r_yx4=0,865>r_уx7=0,758, то для включения в уравнение регрессии оставляем фактор х₄.

Таким образом, проведённый статистический анализ позволил обосновать целесообразность включения в уравнение регрессии двух факторов: х₁ и х₄. Решение о не включении в уравнение регрессии факторов: х₅ и х₈ принято ввиду несущественности их связи с результативным показателем у. а других факторов: х₂, х₃, х₆, и х₇ принято ввиду наличия существенной корреляционной связи между ними с факторами х₁ и х₄.

Пример 4.9.3

Вычислить коэффициенты линейной корреляции между результативными показателями социально-экономическеого состояния населения города Елабуга – у_j; и расходными статьями бюджета - х_i; и по вычисленным значениям построить столбчатые диаграммы. Перечень переменных, отобранных для исследования представлен в таблице 4.9.6.

Таблица 4.9.6. Перечень переменных для примера 4.9.3

Код	Наименование переменной
x1	Статья бюджета “Общегосударственные вопросы” (тыс. руб.)
x2	Статья бюджета “Национальная безопасность и правоохранительная деятельность” (тыс. руб.)
x3	Статья бюджета “Национальная экономика” (тыс. руб.)
x4	Статья бюджета “Жилищно-коммунальное хозяйство” (тыс. руб.)
x5	Статья бюджета “Культура, кинематография и средства массовой информации” (тыс. руб.)
x6	Статья бюджета “Образование” (тыс. руб.)
x7	Статья бюджета “Здравоохранение. Спорт и физическая культура” (тыс. руб.)
x 8	Статья бюджета “Социальная политика” (тыс. руб.)
x 9	Статья бюджета “Межбюджетные трансферты” (тыс. руб.)
z1	Численность населения (тыс. чел.)
z2	Численность населения трудоспособного возраста (тыс. чел.)
z3	Численность работающих на крупных предприятиях (тыс. чел.)
z4	Уровень безработицы (%)
z5	Объем промышленной продукции (млн. руб., до 1997г. – млрд. руб.)
z6	Среднемесячная заработная плата (руб., до 1997г. – тыс. руб.)
z7	Прожиточный минимум на члена семьи (руб., до 1997г. – тыс. руб.)
z8	Стоимость набора из 25 основных продуктов питания (руб., до 1997г. – тыс. руб.)
z9	Обеспеченность населения общей площадью жилья на 1 жителя (кв. м.)
z10	Ввод жилых домов (кв. м. общ. пл.)
z11	Объем реализации платных услуг в расчете на 1 жителя (руб., до 1997г. – тыс. руб.)
z12	Объем реализации бытовых услуг в расчете на 1 жителя (руб., до 1997г. – тыс. руб.)
z13	Оборот розничной торговли на душу населения (руб., до 1997г. – тыс. руб.)
z14	Оборот общественного питания на душу населения (руб., до 1997г. – тыс. руб.)
z15	Обеспеченность населения больничными койками (на 1000 чел.)
z16	Обеспеченность населения врачами (на 1000 чел.)
z17	Обеспеченность населения средним медицинским персоналом (на 1000 чел.)
z18	Общая раскрываемость преступлений (%)
z19	Потребление чистой воды (млн. куб. л.)
z20	Выброс вредных веществ в атмосферу (кг)
z21	Количество автомобилей (шт.)
z22	Отходы животноводческие (тыс. т.)
z23	Отходы бытовые (тыс. т.)
z24	Отходы промышленные (тыс. т.)
y1	Средняя продолжительность жизни (лет)
y2	Рождаемость (тыс. чел.)
y3	Смертность (тыс. чел.)
y4	Естественный прирост (чел.)
y5	Количество зарегистрированных браков (шт.)
y6	Количество расторгнутых браков (шт.)
y7	Разница между заключенными и расторгнутыми браками (тыс. шт.)
y8	Число умерших детей в возрасте до 1 года (на 1000 чел.)
y9	Заболеваемость туберкулезом (на 100 тыс. чел)
y10	Заболеваемость онкологическими заболеваниями (на 100 тыс. чел)
y11	Заболевания органов дыхания (на 1000 чел.)
y12	Заболеваемость системы кровообращения (на 1000 чел.)
y13	Общее количество преступлений (тыс. шт.)
y14	Количество особо тяжких преступлений (тыс. шт.)
y15	Количество тяжких преступлений (тыс. шт.)
y16	Количество преступлений средней тяжести (тыс. шт.)
y17	Количество преступлений небольшой тяжести (тыс. шт.)
y18	Количество умышленных убийств (тыс. шт.)
y 19	Количество причинений вреда здоровью (тыс. шт.)
y20	Количество умышленных причинений тяжкого вреда здоровью (тыс. шт.)
y21	Количество краж (тыс. шт.)
y22	Количество мошенничеств (тыс. шт.)
y23	Количество грабежей (тыс. шт.)
y24	Количество разбоев (тыс. шт.)
y25	Количество вымогательств (тыс. шт.)
y26	Количество неправомерных завладений автомототранспортом (тыс. шт.)
y27	Количество хулиганств (тыс. шт.)

Коэффициент линейной корреляции вычисляется по формуле:

Критическое значение коэффициента линейной корреляции вычисляется по формуле:

,

где t_крит =2.0181 – критическое значение критерия Стьюдента, найдено по статистическим таблицам [11] при n-2 = 44-2=42 степенях свободы и рекомендуемого уровня значимости α=0.05.

Коэффициенты линейной корреляции между результативными показателями и бюджетными факторами представлены в таблице 4.8.7. Таблица 4.9.7. Коэффициенты линейной корреляции между переменными

примера 4.9.3

	х1	x2	x3	x4	x5	x6	x7	x8	x9
y1	-0,35	-0,12	0,44	-0,15	-0.25	-0,49	0,20	-0,27	-0,60
y2	0,46	0,44	-0,31	0,05	0,48	0,62	-0,21	0,57	0,26
y3	0,09	-0,00	-0,34	0,10	0,04	0,25	-0,19	0,09	0,21
y4	-0,43	-0,49	0,05	0,03	-0,50	-0,47	0,06	-0,55	-0,10
y5	0,41	0,20	-0,18	0,01	0,29	0,46	0,08	0,33	0,40
y6	0,11	0,02	-0,02	0,17	0,07	0,08	0,15	0,05	0,39
y7	0,36	0,21	-0,18	-0,16	0,27	0,45	-0,05	0,34	0,08
y8	-0,63	-0,51	0,17	0,08	-0,59	-0,69	-0,05	-0,61	-0,37
y9	-0,60	-0,54	-0,01	0,37	-0,56	-0,60	-0,16	-0,61	-0,09
y10	0,12	-0,19	-0,55	0,20	-0,05	0,30	-0,29	-0,02	0,59
y11	-0,16	-0,01	0,21	-0,25	-0,06	-0,17	0,08	-0,09	-0,34
y12	0,37	0,54	0,34	0,06	0,52	0,22	0,28	0,46	-0,08
y13	0,48	0,33	-0,13	0,18	0,42	0,45	0,07	0,43	0,31
y14	0,24	0,05	-0,07	0,36	0,12	0,15	0,17	0,08	0,35
y15	-0,10	-0,17	-0,04	0,36	-0,14	-0,14	0,04	-0,17	0,13
y16	0,71	0,56	-0,19	-0,06	0,65	0,76	0,03	0,71	0,41
y17	0,56	0,41	-0,26	0,09	0,50	0,62	-0,05	0,54	0,44
y18	0,42	0,48	0,18	-0,01	0,43	0,27	0,35	0,51	-0,05
y19	0,38	0,33	-0,05	0,29	0,38	0,40	0,08	0,40	0,36
y20	0,51	0,36	-0,01	-0,05	0,41	0,44	0,28	0,45	0,23
y21	0,53	0,36	-0,13	-0,01	0,45	0,51	0,08	0,49	0,24
y22	0,43	0,29	-0,13	-0,04	0,36	0,41	0,06	0,40	0,16
y23	0,42	0,49	0,08	0,02	0,50	0,39	0,10	0,54	0,06
y24	0,86	0,64	-0,16	0,04	0,75	0,86	0,21	0,79	0,52
y25	0,32	0,14	-0,24	0,03	0,21	0,32	-0,03	0,20	0,34
y26	0,27	-0,03	-0,22	0,03	0,07	0,26	0,10	0,12	0,25
y27	0,04	0,11	-0,04	-0,11	0,09	0,09	-0,07	0,09	0,02

Приведем диаграммы коэффициентов корреляции для наиболее важных результативных показателей условий жизни на рис. 4.9.2 – рис.4.9.4.

Рис. 4.9.2. Диаграмма коэффициентов корреляции для переменной y₂

Рис. 4.9.3. Диаграмма коэффициентов корреляции для переменной y₁₀

Рис. 4.9.4. Диаграмма коэффициентов корреляции для переменной у₁₃