4.5. Непараметрический показатель связи – коэффициент Фехнера

Простейшим непараметрическим показателем связи является коэффициент Фехнера. Коэффициент Фехнера не требует нормальности распределений случайных величин. В основе его вычисления лежит принцип сопоставления отклонений признаков от своих средних значений. Его применение основано на допущении, что отклонения отклика от своей средней величины должно соответствовать отклонению фактора от своей средней величины. Коэффициент Фехнера вычисляется по формуле:

(4.5.1)

где С – число совпадений знаков отклонений;

Н – число несовпадений знаков отклонений.

Коэффициент Фехнера может принимать значения от -1 до +1. При K_f=±1

связь между признаками х и у функциональная (не случайная). При K_f=0 связь между признаками х и у отсутствует. Промежуточные значения K_f характеризуют степень связи между между признаками х и у.

Пример 4.5.1. Оценить связь объёмов продаж с затратами на рекламу по данным, приведённым в таблице 4.5.1. Средние значения признаков вычислены по следующим формулам:

(4.5.2)

Результаты вычислений сведены в таблицу 4.5.1.

Таблица 4.5.1. Исходные данные и вычисление коэффициента Фехнера

Календарный интервал - i	Затраты на рекламу - xi		Объём продаж - yi		Совпадение отклонений +
1	194	60.7	2560	233.9	+
2	186	52.7	1945	-381.1	-
3	52	-81.3	1450	-876.1	+
4	78	-55.3	1120	-1206.1	+
5	145	11.7	2389	62.9	+
6	178	44.7	4590	2263.9	+
7	130	-3.3	3460	1133.9	-
8	189	55,7	2378	51.9	+
9	89	-44.3	1580	-746.1	+
10	92	-41.3	1789	-537.1	+
Итого:	133.3		2326.1		8 совпадений; 2 несовпадения

По формуле (4.5.1) вычислим коэффициент Фехнера:

Связь между объёмом продаж и затратами на рекламу можно считать прямой и умеренной.

Недостатком коэффициента Фехнера является равенство различных по абсолютной величине отклонений физических значений признаков от средних значений без учёта величины разницы.

4.6. Коэффициенты корреляции рангов

Коэффициенты корреляции рангов можно вычислять как между количественными, так и между качественными признаками при условии, что их можно ранжировать. К ним относятся коэффициенты корреляции рангов Спирмена и Кендалла.

Коэффициент корреляции рангов Спирмена

Для определения тесноты связи как между количественными, так и между качественными признаками, при условии, что они представляют однородные объекты и могут быть ранжированы по одному и тому же принципу можно использовать коэффициент корреляции рангов Спирмена, вычисляемый по формуле:

(4.6.1)

где d_i – разность между величинами рангов аргумента (фактора) и функции (отклика) i – го варианта;

n - количество вариантов.

Если количество вариантов сравнительно велико и их распределение подчиняется нормальному закону, то значимость коэффициента рангов Спирмена можно оценить по критерию Стьюдента по формуле:

(4.6.2)

По статистическим таблицам находится критическое значение критерия Стьюдента t_крит для рекомендуемого уровня значимости α=0,05 при количестве степеней свободы k=n-2. Если t_выч ≥ t_крит то связь между переменными считается существенной. При сравнительно небольших выборках для установления существенности связи между переменными используют специальную таблицу критических значений коэффициента корреляции рангов Спирмена [10].

Пример 4.6.1

Для примера применения коэффициента корреляции рангов Спирмена используем значения затрат на рекламу и объёма продаж, представленные в таблице 4.5.1, введём по ним ранги по возрастанию их значений. Результаты ранжирования представим в таблице 4.6.1.

Таблица 4.6.1. Значения объёмов продаж и затрат на рекламу

Календарный нтервал - i	Затраты на рекламу - xi	Ранг - Rxi	Объём продаж - yi	Ранг - Ryi	di= Rxi - Ryi	di2
1	194	10	2560	8	2	4
2	186	8	1945	5	3	9
3	52	1	1450	2	-1	1
4	78	2	1120	1	1	1
5	145	6	2389	7	-1	1
6	178	7	4590	10	-3	9
7	130	5	3460	9	-4	16
8	189	9	2378	6	3	9
9	89	3	1580	3	0	0
10	92	4	1789	4	0	0

Так как количество вариантов п=10 сравнительно не велико, то для оценки существенности связи воспользуемся специальной статистической таблицей [10], по которой найдём, что при п=10 и рекомендуемом уровне значимости α=0,05 критическое значение ρ_крит=0,634. Так как вычисленное значение ρ_выч превышает критическое значение ρ_крит , то связь между переменными при принятых условиях признаем существенной. Если, например, уменьшить уровень значимости до α=0,02 то критическое значение ρ_крит=0,733. Так как вычисленное значение ρ_выч при принятых условиях не превышает критическое значение ρ_крит, то связь между переменными при принятых условиях признаем несущественной.

При допущении о нормальности распределения переменных вычислим критерий Стьюдента:

По статистическим таблицам найдём критическое значение критерия Стьюдента для рекомендуемого значения уровня значимости α=0,05 и количестве степеней свободы п-2: t_крит=2,31. Так как вычисленное значение критерия Стьюдента превышает критическое, то будем считать связь между переменными существенной.

Коэффициент корреляции рангов Кендалла

Для определения тесноты связи как между количественными, так и между качественными признаками, характеризующие однородные объекты и ранжированные по одному и тому же принципу можно использовать коэффициент корреляции рангов Кендалла, вычисляемый по формуле:

(4.6.3)

где Р_i – количество случаев для i-го варианта (календарного интервала),

ранг которых превышает i-е значение;

Q_i - количество случаев для i-го варианта (календарного интервала),

ранг которых не превышает i-е значение;

n - количество вариантов.

Существенность коэффициента корреляции рангов Кендалла, при условии нормальности распределений случайных величин, проверяют по формуле:

(4.6.4)

Критическое значение критерия Стьюдента находится по статистическим таблицам [10] для рекомендуемого значения уровня значимости α=0,05 и количества степеней свободы п-2.

Пример 4.6.2

Подсчитаем коэффициент корреляции рангов Кендалла для примера 4.5.1. Проведём ранжирование вариантов по рангу R_xi по данным таблицы 4.5.1 и вместе с проведёнными расчётами составим таблицу 4.6.2.

Таблица 4.6.2. Значения объёмов продаж и затрат на рекламу

Календарный нтервал - i	Затраты на рекламу - xi	Ранг - Rxi	Объём продаж - yi	Ранг - Ryi	Pi	Qi	Pi -Qi
3	52	1	1450	2	8	1	8
4	78	2	1120	1	8	0	8
9	89	3	1580	3	7	0	7
10	92	4	1789	4	6	0	6
7	130	5	3460	9	1	4	-3
5	145	6	2389	7	2	2	0
6	178	7	4590	10	0	3	-3
2	186	8	1945	5	2	0	2
8	189	9	2378	6	1	0	1
1	194	10	2560	8	0	0	0

Вычислим коэффициент корреляции рангов:

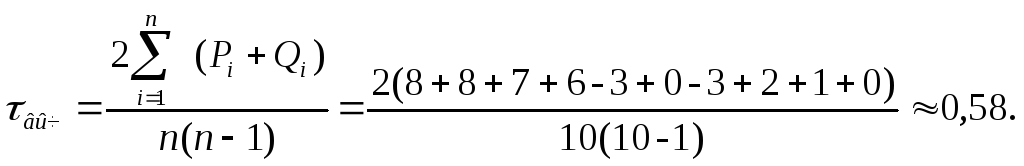
Вычисленное значение положительно и превышает рекомендуемое значение 0,50, что указывает на наличие существенной зависимости между переменными.

При допущении о нормальности распределений исходных данных существенность коэффициента корреляции рангов Кендалла проверим по формуле (4.6.4):

Критическое значение критерия Стьюдента находится по статистическим таблицам для рекомендуемого значения уровня значимости α=0,05 и количества степеней свободы п-2 [10]: t_крит=2,31.

Так как τ_выч = τ_крит то делаем заключение о наличии существенной связи между переменными.