Метод моментов для равномерного закона

ФП и ФР равномерного закона:

. (3.17)

Вычислим первый и второй начальные моменты:

(3.18)

(3.19)

Вычислим стандартное отклонение и параметры равномерного закона:

(3.20)

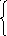
(3.21)

(3.22)

Вычислим вероятность попадания случайной величины в интервалы гистограммы и гипотетическую ФР:

(3.23)

(3.24)

Следует учитывать, что при построении гистограммы принимается:

; .

Пример3.1. Аппроксимация экспериментального распределения случайных чисел равномерным законом с оценкой качества аппроксимации по критерию согласия Колмогорова

Экспериментальное распределение представляет собой выборку, состоящую из 10 трёхразрядных чисел, поэтому проведём аппроксимацию с оценкой качества аппроксимации по КС Колмогорова. Представим распределение случайных чисел по возрастанию их значений: 137, 221, 353, 366, 367, 507,686, 905, 918, 985 и построим по нему эмпирическую ФР, представленную на рис.3.2.

Вычислим основные характеристики эмпирического распределения:

.

сек.

сек.

Рис.3.2. Эмпирическая и гипотетическая функции распределения

Вычислим параметры равномерного закона:

сек.

сек.

По двум найденным точкам построим прямую линию, которая является гипотетической ФР. Она изображена на рис.3.2. По рис.3.2 находим, что максимальная разница между эмпирической и гипотетической ФР при аргументе, равном 367. Уточним значение ФР для этого значения и вычислим КС Колмогорова:

По статистическим таблицам находим коэффициент доверия высказанной гипотезе: _.

Вывод: имеющиеся статистические данные не противоречат гипотезе о их подчинении равномерному закону по КС Колмогорова.

Пример3.2. Аппроксимация экспериментального распределения 100 одноразрядных чисел равномерным законом с оценкой качества аппроксимации по КС Пирсона

Выборка из 100 случайных чисел представлена в виде совокупности, состоящей из 5 строк и 20 столбцов.

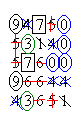
Подсчитаем количество символов каждого типа и построим гистограмму, представленную на рис.3.3.

Рис.3.3. Гистограмма распределения 100 одноразрядных случайных чисел

Вычислим основные статистические характеристики распределения, параметры закона, значение КС Пирсона и по статистическим таблицам определим коэффициент доверия, выдвинутой гипотезе:

Ввиду того, что найденный коэффициент доверия не укладывается в рекомендуемый 10% - й доверительный интервал то гипотезу ввергаем.

Отметим, что если бы чисел «2» было 9, а не 5; а чисел «4» было бы 13, а не 17, то было бы равно:

² ={1+4+1+16+9+4+16+4+16+4+25}/10=8,4;

при R=7; тогда по статистическим таблицам находим р=0,31 и гипотеза не отвергается.

Метод моментов для экспоненциального закона

В теории массового обслуживания центральное место занимает экспоненциальный закон, благодаря своим следующим замечательным свойствам.

1. Ординарности, которая заключается в том, что если в ОМ действует несколько экспоненциальных законов, то в любой момент времени в такой системе не может произойти более одного события.

2. Стационарности (независимости от времени). Стационарный режим в простейшей системе наступает тогда, когда выполняется условие, что интенсивность поступления транзактов  не превышает интенсивности их обслуживания . В таких системах через некоторое время, которое называют переходным режимом, процесс изменения состояния системы перестает зависеть от времени и зависит только от технических характеристик ОМ и параметров внешней среды, в которой он функционирует. Условие наличия стационарного режима для простейшей СМО .

3. Отсутствия последействия, которое заключается в том, что время, оставшееся до окончания экспоненциального процесса в любой момент его протекания распределено по экспоненциальному закону с той же интенсивностью, с которой распределено все распределение случайных чисел.

Эти три свойства позволяют строить Марковские цепи, являющиеся основой аналитического моделирования СМО.

Функция распределения (ФР) экспоненциального закона приведена на рис.2.4. Это вероятность того, что случайная величина Х не превысит своего текущего значения х.

F(x)

F(x₁) F(x)P{Xx}

x₁ х

Рис.3.4. Функция распределения экспоненциального закона

Функция плотности (ФП). Это плотность вероятности случайной величины,

или дифференциальная функция распределения. ФП экспоненциального закона приведена на рис.3.5.

f(x)

f(x)=F^/(x)



x

Рис. 3.5. Функция плотности экспоненциального закона

Экспоненциальный закон имеет диапазон своего существования от 0 до . Функция плотности экспоненциального закона

. (3.25)

ФР экспоненциального закона можно вычислить по ФП:

(3.26)

ФП экспоненциального закона определяется всего одним параметром m. Для потоков событий это количество транзактов (заявок), поступающих за единицу времени. Для процессов обслуживания – это количество транзактов, которое может быть обслужено при их непрерывном поступлении в обслуживающий аппарат (ОА). Вычислим первый начальный момент по функции плотности:

(3.27)

Для вычисления интеграла (3.27) проведём интегрирование по частям:

Пусть , тогда ;

Рассмотрим этот же интеграл с пределами и вычислим основные статистические характеристики экспоненциального закона:

(3.28)

В полученном математическом выражении отдельно рассмотрим первое слагаемое:

Для первого слагаемого получили неопределённость вида бесконечность на бесконечность. Раскроем его по правилу Лопиталя, взяв отдельно производные от числителя и знаменателя.

Таким образом, первое слагаемое в (2.28) можно отбросить и вычислить интеграл по второму слагаемому.

(3.29)

Получили формулу для вычисления интенсивности экспоненциального закона по экспериментальным данным.

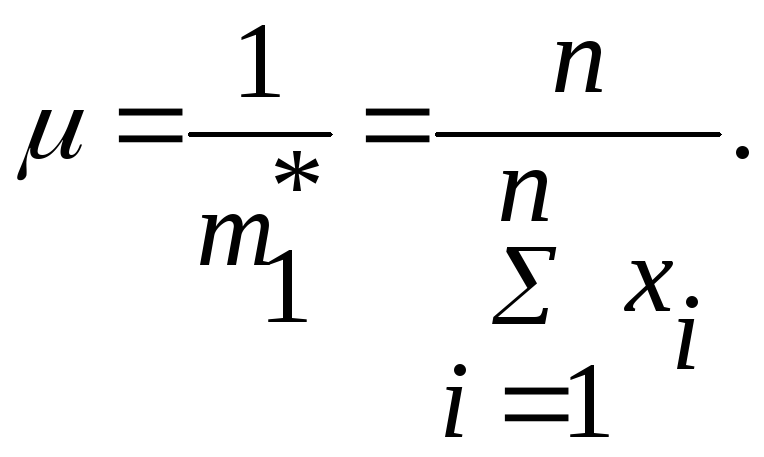(3.30)

Вычислим второй начальный момент:

(3.31)

Пусть , тогда ;

Рассмотрим этот же интеграл с пределами и вычислим основные статистические характеристики экспоненциального закона:

(3.32)

В полученном математическом выражении (3.32) отдельно рассмотрим первое слагаемое:

(3.33)

Для первого слагаемого выражения (3.33) получили неопределённость вида бесконечность на бесконечность. Раскроем его по правилу Лопиталя, взяв отдельно производные от числителя и знаменателя.

(3.34)

Снова получили неопределённость вида бесконечность на бесконечность. Снова раскроем его по правилу Лопиталя, взяв отдельно производные от числителя и знаменателя.

(3.35)

Таким образом, первое слагаемое можно отбросить и вычислить интеграл по второму слагаемому.

(3.36)

Вычислим среднее квадратическое отклонение.

(3.37)

Для вычисления значений КС по формулам (3.8) и (3.11) требуется предварительно вычислить вероятности попадания случайной величины в интервалы гистограммы и гипотетические функции распределения по следующим формулам.

(3.38)