30

Лекция 3 Аппроксимация экспериментальных распределений случайных чисел стандартными статистическими законами

На практике для аппроксимации наиболее часто применяются методы моментов максимального правдоподобия.

Метод моментов аппроксимации экспериментальных распределений стандартными статистическими законами

Суть метода моментов заключается в приравнивании оценок моментов, вычисленных по экспериментальным данным, соответствующим им моментам, вычисленным по функции плотности или моментной производящей функции (МПФ). Качество представления рекомендуется оценивать по критериям согласия. Для применения метода момента требуется выполнить следующие действия.

1. На основании физической сущности анализируемого случайного процесса высказывается гипотеза о его подчинении какому-то стандартному статистическому закону. Для выбранного закона, который называется гипотетическим, записывается функция плотности или МПФ и определяется количество параметров гипотетического закона - d.

2. По экспериментальным данным вычисляются оценки начальных моментов. Если все случайные значения равновероятны, то используются следующие формулы для вычисления оценок начальных моментов:

, (3.1)

где s – порядок момента ();

n – количество реализаций случайной величины.

Оценка математического ожидания (первого начального момента) вычисляется по формуле:

. (3.2)

Оценка второго начального момента вычисляется по формуле:

. (3.3)

Оценки центральных моментов вычисляются по формуле:

(3.4)

Оценка второго центрального момента (дисперсии) определяется по формуле:

. (3.5)

Оценка среднего квадратического отклонения (стандартного отклонения) определяется по формуле:

. (3.6)

На практике обычно оценку стандартного отклонения вычисляют по оценкам второго и первого начального моментов.

. (3.7)

При количестве случайных чисел n в выборке (частная выборка), стремящемуся к бесконечности (к генеральной совокупности) n→ ∞; оценки начальных моментов стремятся к соответствующим им моментам .

3. Записываем формулы для вычисления моментов по ФП и составляем систему уравнений, решение которой определит значения параметров гипотетического закона. Таким образом, система должна состоять из d уравнений, но в любом случае, если даже d=1 рекомендуется определять не менее 2-х первых моментов и их оценок.

4. Оцениваем качество аппроксимации по критериям согласия (КС), среди которых наибольшее применение получили ² (Пирсона) и критерий Колмогорова-Смирнова.

4.1. Для использования ² строится гистограмма распределения случайной величины на основе группировки случайных чисел так, как это показано на рис. 3.1.

Рис.3.1. Гистограмма распределения случайной величины х

в диапазоне от a до b

КС ² вычисляется по формуле:

(3.8)

с количеством степеней свободы

R=L – d – 1, (3.9)

где L – количество интервалов гистограммы;

экспериментальная i-я частота, то есть количество попаданий случайной величины в i-й интервал гистограммы;

гипотетическая частота, то есть количество случайных чисел, которое должно было попасть в i-й интервал гистограммы:

;

n – количество реализаций случайной величины;

P_i – вероятность попадания случайной величины в i-й интервал гистограммы;

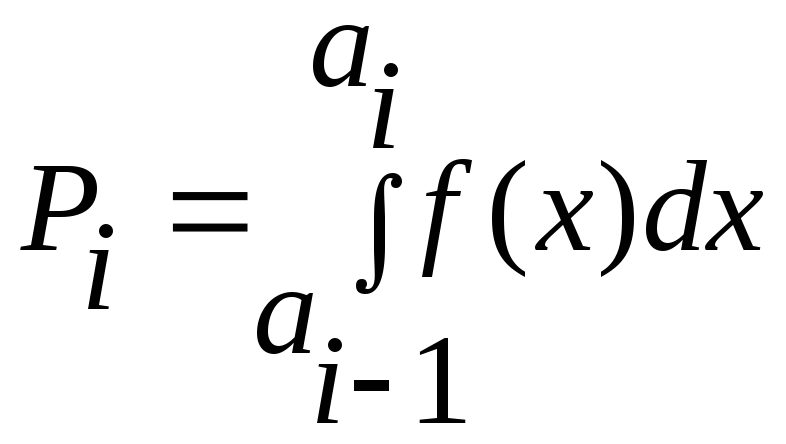, (3.10)

где а_i-1, a_i – левая и правая границы i-го интервала гистограммы;

R – количество степеней свободы (разница между количеством имеющихся интервалов гистограммы и определяемыми параметрами).

По вычисленным значениям ² и R по статистическим таблицам определяется коэффициент доверия гипотезе - Р_р, который должен укладываться в 10% доверительный интервал т.е. должно выполняться неравенства. Если это условие выполняется, то делается заключение, что имеющиеся статистические данные не противоречат гипотезе об их подчинении высказанному гипотетическому закону по КС Пирсона. Если данное неравенство не выполняется, то гипотезу рекомендуется отвергнуть и провести аппроксимацию другим законом, как правило, более сложным.

Для корректного применения КС ² рекомендуется строить гистограммы с количеством интервалов не менее 7 и чтобы количество попаданий случайной величины в любой интервал гистограммы, было не меньше 7. Таким образом, для использования КС ² требуется наличие не менее 49 случайных чисел.

4.2. При сравнительно небольшом количестве случайных чисел рекомендуется применять КС Колмогорова, который вычисляется по формуле:

(3.11)

где n - количество реализаций случайной величины;

эмпирическая и гипотетическая функции распределения.

Эмпирическая функция распределения строится по имеющейся последовательности случайных чисел. Каждая имеющаяся случайная величина увеличивает функцию распределения на величину 1/n. Таким образом, функция распределения представляется графиком, изменяющимся от 0 до 1. Значения гипотетической функции распределения вычисляются по формуле:

, (3.12) ,

где а – левая граница диапазона существования закона.

КС Колмогорова-Смирнова не допускает какой-либо группировки случайных событий и требует, чтобы каждое из имеющихся случайных чисел было проверено на поиск максимума индивидуально. По вычисленному значению К по статистическим таблицам находится коэффициент доверия гипотезе Р_К, который должен удовлетворять условию:

Р_К  0,20.

Если данное условие выполняется, то делается заключение, что имеющиеся статистические данные не противоречат гипотезе об их подчинении высказанному гипотетическому закону по КС Колмогорова. В противном случае гипотезу рекомендуется отвергнуть.

Метод максимального правдоподобия аппроксимации эксперимен-

тальных распределений стандартными статистическими законами

Суть метода максимального правдоподобия заключается в нахождении таких значений параметров статистического закона, при которых функция подобия достигает своего максимального значения. Качество представления рекомендуется оценивать по критериям согласия. Для применения метода максимального правдоподобия требуется выполнить следующие действия.

1. На основании физической сущности анализируемого случайного процесса высказывается гипотеза о его подчинении какому-то стандартному статистическому закону. Для выбранного закона, который называется гипотетическим, записывается функция плотности, которая определяет количество параметров гипотетического закона - d.

2. По экспериментальным данным для каждого параметра статистического закона составляется функция правдоподобия:

L(x₁,x₂,…x_n;p₁,p₂,···p_d)=f(x₁, p₁,p₂,···p_d)·f(x₂, p₁,p₂,···p_d)···f(x_n, p₁,p₂,···p_d), (3.13)

где f(x_i, p₁,p₂,···p_d) – значение функции плотности, определяемой параметрами p₁,p₂,···p_d, в i-ой точке экспериментального распределения случайных чисел;

x_i – значение случайной величины в i-ой точке экспериментального распределения случайных чисел;

p_j - j – параметр гипотетического закона распределения случайных чисел;

n – количество значений экспериментального распределения случайных чисел;

d – количество параметров гипотетического закона распределения случайных чисел.

3. Рекомендуется, но не обязательно, прологарифмировать функцию правдоподобия:

Ln(L(x₁,x₂,…x_n;p₁,p₂,···p_d))=ln(f(x₁, p₁,p₂,···p_d))+ln(f(x₂, p₁,p₂,···p_d))+···+

+ln(f(x_n, p₁,p₂,···p_d)). (3.14)

4. Составляется система уравнений в частных производных по параметрам статистического закона от функции правдоподобия, которые приравниваются нулю:

∂ L(x₁,x₂,…x_n;p₁,p₂,···p_d)=0; (3.15)

∂p_j

Вместо функции правдоподобия можно использовать логарифмическую функцию подобия:

∂ ln(L(x₁,x₂,…x_n;p₁,p₂,···p_d))=0; (3.16)

∂p_j

5. Решением системы уравнений (3.15) или (3.16) находятся параметры статистического закона.

6. Качество аппроксимации оценивается по критериям согласия ² и Колмогорова-Смирнова, по методике, описанной в предыдущем разделе.