книги / Теория автоматического управления. Дискретные системы

или полные суммы

m=0

В качестве аналогов дифференциальных уравнений в дискретных САУ рассматриваются уравнения в конечных разностях.

При использовании обратных разностей уравнение в конечных разностях будет иметь вид

b0 m y[n]+b1 m−1 y[n]+...+bm y[n]= f [n] .

С учетом (2.1) последнее выражение приобретает вид

a0 y[n]+a1 y[n −1]+...+am y[n −m]= f [n] ,

где коэффициенты уравнения определяются выражениями

2.2. Преобразование Лапласа дискретных функций

Введем в рассмотрение дискретных сигналов понятие импульсной функции (см. рис. 2.1):

n=0

являющейся последовательностью модулированных по амплитуде импульсов на выходе идеального импульсного элемента.

Хотя эта функция имеет бесконечно большие ординаты, мы можем считать их пропорциональными ординатам f[nT] с коэффициентом пропорциональности 1/γT, где γ – скважность бесконечно тонкого прямоугольного импульса.

Преобразование Фурье (частотный спектр) для одного импульса δ(t – nT) равно e–jωnT, поэтому спектр определяется, как

21

Вынесем f[nT]e–pt за знак интеграла, заменив дискретными значениями, так как только при этих значениях δ(t) отличается от нуля:

Интеграл от δ-функции в бесконечных пределах равен 1, поэтому имеем

n=0

Спектр и изображения сигнала f*(t) в выражениях (2.5) и (2.8) определяются дискретными значениями f[nT].

В приведенных формулах, как и в случае непрерывного преобразования Лапласа, комплексная величина p = c + jω, где с – абсцисса абсолютной сходимости. Если с < ∞, то ряд, определяемый формулой (2.8), сходится и решетчатой функции соответствует ее изображение. Процедура определения F*(p) по (2.8) называется

дискретным преобразованием Лапласа (D-преобразованием).

Введением новой переменной z = epT в уравнение (2.8) осуществляется переход от дискретного к Z-преобразованию Лапласа для дискретных значений сигнала f[nT] = f[n]:

n=0

Преобразование (2.8) существует для тех значений z, которые удовлетворяют условию | z | > R = 1/ρ, где ρ – радиус сходимости ряда.

22

Процедуры определения значений D- и Z-преобразований Лапласа символически отображаются, как D{f[nT]} = F*(p) и Z{f[n]} = F(z).

Решетчатые функции в общем случае могут быть смещенными во времени от моментов квантования, которые выражаются f[(n + ε)T] или f[n + ε], где 0 ≤ ε ≤ 1, тогда преобразование называется моди-

фицированным или смещенным.

Z-преобразование смещенной решетчатой функции в этом случае будет иметь вид

n=0

Пример 2.1. Определить Z-изображение единичной ступенчатой решетчатой функции f[nT] при T = 1 c.

1(t) – огибающая решетчатой функции, для которой непре-

рывное преобразование Лапласа L{1(t)}= 1p .

Решетчатая функция f [n]=

Знаменатель прогрессии q = z–1. Тогда для |z| > 1

23

постоянная, в общем случае, комплексная величина, T = 1 c. Проделав действия, аналогичные действиям в примере 2.1, получим

где d = e–αT.

В табл. 2.1 приведены непрерывное и Z-преобразования Лапласа типовых непрерывных функций.

24

2.3.Основные свойства и теоремы Z-преобразования

1.Свойство линейности. Изображение линейной комбинации решетчатых функций равно той же линейной комбинации их изображений:

25

2. Теорема запаздывания (сдвиг на целое число тактов впра-

во). Пусть имеем смещенную решетчатую функцию f[n–m], запаздывающую на целое число тактов m. Если обозначить n–m = r, то

m

= z−m[F(z) +∑f [−r]zr ].

r=1

Если исходная решетчатая функция f[n] равна нулю при отрицательных значениях аргумента, то Z{f[n–m]} = z −m F(z) .

Пусть смещение решетчатой функции в сторону опережения на m тактов, тогда, проведя замену n + m = r, получим Z-преобразо- вание:

m−1

= zm F (z)−zm ∑f [r]z−r .

r=0

Второе слагаемое в правой части полученного уранения обращается в нуль, если f[n]≡0 при n=0,1,…, m–1.

3. Изображение разностей. Для первой обратной разности

Z{ f [n]}=Z{ f [n]− f [n−1]}=

=F(z) −z−1F(z) −z−1 f [−1]z = z −z 1F(z)− f [−1],

так как для отрицательных аргументов решетчатая функция тожде-

ственно равна нулю, то Z{ f [n]}= z −z 1F(z), также и для k-й об-

ратной разности, когда

26

f[n] ≡ 0 при n<0

Z{ k f [n]}= z −z 1 k F(z) .

Для прямых разностей может быть записано похожее предыдущему выражение при равенстве нулю решетчатой функции в первых k-х точках

Z{∆ kf[n]} = (z–1)kF(z).

4. Изображение сумм. Составим прямую разность для неполной суммы

∆σ[n] = σ[n+1] – σ[n] = f[n].

На основании изображения прямой разности имеем

Z{σ[n]} = F(z)/(z–1),

для k-кратного суммирования Z{σ k[n]}=F(z)/(z–1)k. Изображение k-кратной полной суммы

Z{σ0k[n]}=(z/(z–1))kF(z).

5. Начальное значение решетчатой функции. Если решетча-

тая функция f[n] имеет преобразование F(z) и предел этой функции при z→∞ существует, то

f [0]=lim f [n]=lim F (z).

n→0 z→∞

Доказательство находится из определения Z-преобразования:

F(z)= f(0)+ f(T)/z+f(2T)/z2+ f(3T)/z3+…,

откуда вытекает очевидное вышеприведенное равенство пределов.

6. Конечное значение решетчатой функции. При условии,

что предел f[n] существует и преобразование F[z] не имеет полюсов |z|≥1, имеем

27

=limn→∞ − f (0)+ f (1)(1−z−1 )+ f (2)(z−1 −z−2 )+...

...+ f (n)(z−n+1 −z−n )+ f (n +1)z−n .

Тогда

при условии, что предел в правой части существует. Кроме того, по теореме о сдвиге

Z {[f (i +1)]−[f (i)]}= z[F (z)− f (0)]−F (z)=(z −1)F (z)−zf (0).

Полагая в этом выражении z→1 и приравнивая его предыдущему, имеем

существует.

Как и в случае теоремы о конечном значении в непрерывном преобразовании Лапласа, предел в правой части может дать неверное значение, если предел в левой части не существует.

28

2.4. Вычисление решетчатых функций

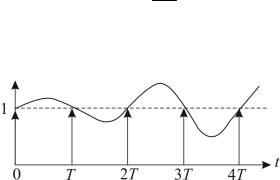
Процедура обратного преобразования Лапласа для определения оригинала непрерывной функции по ее изображению является однозначной, чего нельзя сказать о дискретных (решетчатых) функциях. Если для функции f(t) имеется изображение F(z), то обратное Z-преобразование не обязательно равно f(t). Корректный результат обратного Z-преобразования функции F(z) есть f[nT], который равен f(t) только в моменты квантования t=nT. Это ограничение необходимо учитывать при применении метода. На рис. 2.2 приведена иллюстрация факта, что для Z-преобразования единич-

ной ступенчатой функции, равной z z−1 и соответствующей после-

довательности единичных импульсов, обратное Z-преобразование может быть любой функцией, значения которой равны единице в моменты t=0, T, 2T,…

Рис. 2.2. Неоднозначность обратного Z-преобразования

Для вычисления решетчатой функции по ее изображению могут быть использованы методы: обратное преобразование Z-изобра- жения решетчатой функции; разложение формул; разложение

встепенной ряд; разложение на простые дроби.

1.Обратное преобразование Z-изображения решетчатой функции. Данная процедура определения оригинала решетчатой

функции заключается в определении последовательности f[n] и обозначается как Z –1{F(z)}.

Для решения данной задачи используется формула обраще-

ния:

29

Так как z = exp(pT) и dz = Tzdp, то формула обращения примет вид

Интегрирование ведется по окружности с центром в начале

координат и радиусом R > |zν|max, где ν=1,2,…,l; zν – полюсы функции F(z).

Полученное выражение для практического использования оказывается сложным в общем случае полюсов функции F(z).

В частном случае простых полюсов значение интегрального вычета в точке z=zν определяется по формуле

Resv F (z)zn−1 = zlimz (z −zv )F (z)zn−1.

→ v

люсы функции F(z) простые и имеют значения z = 1 и z = d = e–αT. Получим выражение решетчатой функции

=1−d n =1−e−αn .

2. Формулы разложения. Пусть изображение представляет собой отношение многочленов

F (z)= BA((zz)) = zAB0((zz)),

30