книги / Теория автоматического управления. Дискретные системы

7.2.5. Синтез цифровой обратной связи

Требуемое качество дискретной системы управления можно обеспечить путем включения цифрового регулятора в цепь обратной связи, как показано на рис. 7.4, г. В качестве регулятора могут быть использованы, например, цифровые датчики с цифроаналоговыми преобразователями.

Пусть в дискретной системе, как показано на структурной схеме рис. 7.4, г, применена цифровая обратная связь, причем ее передаточную функцию примем одинаковой структуры с цифровым последовательным регулятором, полученным в результате синтеза с заданной колебательностью системы в подразд. 7.2.2.

Моделирование системы выполнено по нижеприведенному скрипту:

num=[100];den=[0.1 1 0]; sys=tf(num,den); sys1=c2d(sys,0.01,'zoh') sys2=tf([-4.33 4.33],[1 0],0.01); sys7=feedback(sys1,-sys2) zero(sys7),pole(sys7) sys9=feedback(sys7,1) zero(sys9),pole(sys9) [y,t]=step(sys9,0:0.01:0.25);

plot(t,y),title('h(t) системы с цифровой обратной связью') xlabel('время,с'),ylabel('h(t)')

grid

С целью сохранения порядка астатизма в системе при охвате объекта обратной связью регулятор должен быть дифференцирующего типа. С учетом передаточного коэффициента типового регулятора для обратной связи, вычисленного по (7.25), D-регулятор принят с передаточной функцией, как показано в вышеприведенном скрипте с передаточной функцией

141

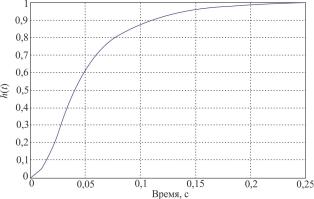
Рис. 7.13. Переходная характеристика с цифровой обратной связью

Переходная характеристика системы по результатам моделирования приведена на рис. 7.13, которая имеет в отличие от рис. 7.7 монотонный характер, при этом наблюдается незначительное увеличение времени регулирования (с 0,075 до 0,13 с).

7.3. Синтез цифровых систем с апериодическим переходным процессом

К большинству систем управления в числе основных показателей качества предъявляется требование обеспечения быстродействия. Такой класс систем управления называется системами с ми-

нимальным временем переходного процесса.

В основу синтеза таких систем управления положен принцип компенсации нулей и полюсов передаточной функции управляемого процесса полюсами и нулями цифрового регулятора с добавлением полюсов и нулей в соответствующих местах на z-плоскости.

При малых значениях периода квантования дискретный процесс практически совпадает с непрерывным, «пульсаций» в промежутках между моментами квантования нет. Такой процесс обычно называют апериодическим.

142

Пусть передаточная функция замкнутой системы с последовательным регулятором имеет вид

где WО(z) – передаточная функция управляемого процесса. Разрешаем уравнение (7.26) относительно передаточной

функции регулятора:

Представим z-преобразование входного сигнала в виде функ-

ции:

где N – положительное целое число;

A(z) – полином от переменной z−1, не имеющий нулей z=1. Например, для единичной ступенчатой входной функции A(z)=1

иN=1; для единичной линейной входной функции A(z)=Tz–1и N=2

ит.д. В общем случае выражение (7.29) соответствует входным сигналам типа t N–1.

Приравняем к нулю установившуюся ошибку:

Поскольку полином A(z) не содержит нулей z=1, то необходимым условием равенства нулю установившейся ошибки является

наличие множителя (1− z−1 )N в выражении 1−Wз (z). Следовательно, последнее должно иметь вид

где F(z) – полином от переменной z–1.

Разрешая уравнение (7.31) относительно 1−Wз (z), получим

Так как F(z) является полиномом от z–1, то она имеет полюсы только z=0. Таким образом, выражение (7.32) показывает, что характеристическое уравнение системы с нулевой установившейся ошибкой имеет вид

где p – положительное целое число, причем p ≥ N.

Изображение ошибки в системе после подстановки (7.31) в (7.28) будет

E(z)=A(z)F(z). (7.34)

Как уже было отмечено, поскольку A(z) и F(z) являются полиномами от z–1, то E(z), определяемое выражением (7.34), будет иметь конечное число членов при разложении его в ряд по отрицательным степеням z. Поэтому, если характеристическое уравнение цифровой системы управления имеет вид (7.33), т.е. все его корни нулевые, то сигнал ошибки будет сводиться к нулю за конечное число периодов квантования.

В общем случае F(z) может иметь вид отношения полиномов

от z:

144

где Fn (z) и Fd (z) – полиномы, не содержащие полюсов и нулей

z=1, а также полюсов, для которых |z|>1.

Тогда характеристическое уравнение будет иметь вид

При синтезе цифровых регуляторов любым методом требуется обеспечение их физической реализуемости. В данном случае передаточная функция регулятора находится по (7.27), при этом накладываются на нее ограничения: если передаточные функции управляемого процесса и замкнутой системы могут быть разложены вряд

WО (z)= fn z−n + fn+1zn−1 +....

Wз (z)= gk z−k + gk +1g−k −1 +...,

где n ≥ 0 и k ≥ 0.

Подставив эти выражения в (7.27), получим передаточную функцию регулятора:

= dk −n z−(k −n) + dk −n+1z−(k −n+1) +....

Таким образом, для физической реализуемости регулятора необходимо выполнение условия k ≥ n. При этом условии выбор функции F(z) должен проводиться по уравнению (7.31). В действительности принимают простейшую функцию, не противоречащую условиям (7.31) – F(z)=1 для всех видов простейших типовых входных воздействий.

Тогда с учетом (7.32) будем иметь функции (1−Wз (z)):

• при единичном ступенчатом входном воздействии (N=1) – z–1;

145

•при единичном линейном входном воздействии (N=2) –

–2z–1 – z–2;

•при параболическом входном воздействии (N=3) – 3z–1 – 3z–2 +

+ z–3.

Из метода синтеза регуляторов непрерывных систем известна недопустимость полной компенсации нулей и полюсов передаточной функции управляемого процесса по соображениям их помехозащищенности и устойчивости.

Рассмотренный метод является примером получения идеального апериодического процесса, который относится к определенному закону изменения входного воздействия и предполагает неизменность параметров системы.

Реальные управляемые процессы могут предусматривать любой закон изменения входного сигнала и наличие на единичной окружности или вне ее нулей или полюсов передаточной функции. Кроме того, системы с апериодическим переходным процессом очень чувствительны к изменениям параметров.

Рассмотренный метод компенсации нулей и полюсов управляемого процесса практически осуществляется введением весового коэффициента в желаемую передаточную функцию замкнутой

системы Wз (z), что соответствует введению дополнительного по-

люса в передаточную функцию замкнутой системы. Модифицируем функцию

где c – полюс, значения которого ограничены диапазоном от –1 до

1из условия устойчивости функции Wзм (z).

Впроцессе синтеза цифрового регулятора определяется значение с, обеспечивающее удовлетворительные показатели качества переходного процесса (наряду с минимальной длительностью допустимое перерегулирование).

146

Пример 7.4. Пусть управляемый процесс в цифровой системе с экстраполятором нулевого порядка описывается передаточной

Так как объект имеет нуль вне единичной окружности и один нулевой полюс, синтез регулятора проведем с введением весового коэффициента.

Принимая функцию F(z)=1 при единичном ступенчатом воздействии получим модифицированную желаемую передаточную функцию замкнутой системы по уравнению (7.38):

1−Wзм (z)= 1−− z−−11 . 1 cz

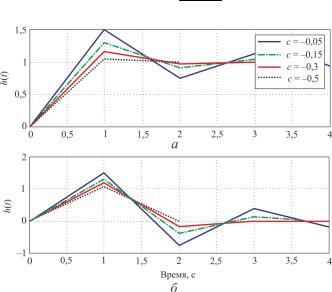
Рис. 7.14. Переходная (а) и импульсная (б) характеристики с дополнительным полюсом

147

ничных ступенчатом и импульсном входных воздействиях. По полученным временным характеристикам на рис. 7.14 видно, что система устойчива и переходные процессы практически затухают независимо от типа входного воздействия за 2 периода квантования при введенных дополнительных полюсах с ≤ –3.

7.4. Синтез цифрового регулятора на основе имитационного моделирования

По сравнению с инженерными методами, основанными на применении графоаналитических способов определения динамических свойств систем автоматического управления и их практической реализации, аналитические методы при меньшей наглядности, обладают большей точностью результатов. К числу аналитических методов относятся машинные методы расчета, которые позволяют сформулировать задачу определения параметров, соответствующих требуемым динамическим свойствам. По существу задача сводится к построению области, внутри которой выбранный критерий отвечает заранее поставленным условиям.

Алгоритм показан на примере синтеза ПД-регулятора в цифровой системе с астатическим объектом, рассмотренным в примере 7.1.

В качестве критерия примем квадратичный интегральный критерий от переходной составляющей системы с эталонной моделью:

где kп,kд – параметры настроек выбранного ПД-регулятора.

Понятно, что идеальным эталонным процессом будет воздействие в виде ступенчатого сигнала, однако чрезмерное быстродействие в системе приводит к недопустимым и практически нереали-

148

зуемым перенапряжениям и перегрузкам. В связи с этим эталонной моделью принято линейное динамическое звено первого порядка с постоянной времени τ = 0,1 c, которая выбрана из диапазона рекомендуемых значений tп/6 ≤ τ ≤ tп/3 и длительности апериодического переходного процесса объекта (4...5)То.

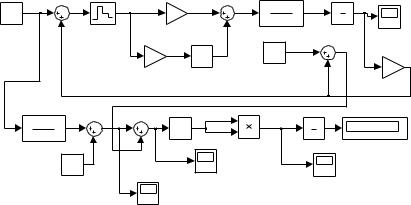
Схема имитационной модели системы для определения настроек регулятора в Simulink приведена на рис. 7.15.

Scope 1

Рис. 7.15. Схема исследуемой системы в Simulink

Поиск оптимальных параметров настройки регулятора можно провести наиболее эффективным из известных методов поиска экстремума – методом деформируемого многогранника (симплексный метод Нелдера – Мида). Поскольку задачей оптимизации не является изучение методов оптимизации, определение настроек регулятора выполнено простейшим методом при двух параметрах – методом покоординатного спуска.

Для принятой исходной системы переходный процесс на рис. 7.5 соответствует параметрам ПИ-регулятора kп =1, kд = 0.

Поиск параметров ведется вначале по kп уменьшением его значений с интервалом 0,1. При значении коэффициента 0,1 достигается локальный экстремум F (0,1;0) = 0,0176. Следующие поис-

149

ковые шаги проводим по kп с интервалом увеличения 0,01.

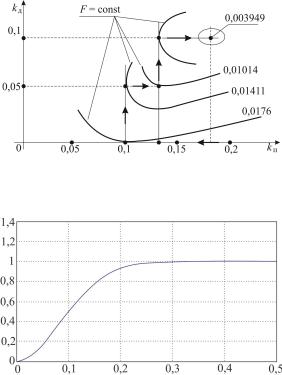
На рис. 7.16 приведена схема пошаговой процедуры определения минимума интегрального критерия в функции параметров настройки регулятора.

Поиск экстремума завершается при его значении F(0,18;0,085) = = 0,003949.

Рис. 7.16. Схема определения экстремума интегрального критерия

Рис. 7.17. Переходный процесс оптимизированной системы

Результат моделирования системы с вычисленными параметрами настройки регулятора (kп = 0,18, kд = 0,085) приведен

на рис. 7.17. Получен монотонный переходный процесс длительностью 0,21 с.

150