
книги / Сопротивление материалов. Статические прочностные расчёты
.pdf
|
|
|
|
|
EIy |
|
|
= 0, |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
x =2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
= 0. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
EIy |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x =4 |
|
20 24 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
EIy |
|
= EIy0 + EIθ0 2 − |
= 0, |
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
x =2 |
|
|
|
|
24 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
EIy |
|
= EIy0 + EIθ0 4 − |
20 24 |
+ |
20 24 |
+ 30 |
22 |
|
+ |
10 23 |
+ |
10 13 |
= 0 |
||||||
|
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
x=4 |
24 |
24 |
2 |
|
6 |
6 |
|
||||||||||
|
|
|
|
|
|||||||||||||||
или
EIy0 + 2EIθ0 −13,3 = 0,
EIy0 + 4EIθ0 −125 = 0.
Решая эту систему уравнения, получаем
EIθ0 = 55,85 кН м2 ; EIy0 = −98, 4 кН м3 .
Необходимо отметить, что в первом уравнении системы учитывается только нагрузка, действующая слева от опоры A (в которой прогиб равняется нулю); а во втором – нагрузка, действующая слева от опоры B (в которой прогиб также равняется нулю).
После подстановки начальных параметров получаем универсальное уравнение изогнутой оси балки или уравнение прогибов:
|
|
|
|
|
x4 |
|
|
( x − 2)4 |
|
( x − |
2)2 |
|||
EIy = −98, 4 + 55,85x − q1 |
|
|
|
+ q1 |
|
+ M |
+ |
|||||||
24 |
24 |
|||||||||||||
|
|
|
|
|
|
|
|
2 |
||||||
+RA |
( x − 2)3 |
+ p |
( x − |
3)3 |
+ RB |
( x − 4)3 |
− q2 |
( x − 4)4 |
||||||
6 |
|
|
|
|
6 |
24 |
. |
|||||||
|
|
|
|
|||||||||||
|
6 |
|
|
|
|
|
|
|
|
|||||
Находим величину EJy в точке C балки:
51

EIy |
|
|
|
|
= −98, 4 + 55,85 6 − 20 |
64 |
|
+ 20 |
44 |
|
+ 30 |
42 |
+ |
|||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
x =6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
24 |
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
+10 |
43 |
|
+10 |
33 |
|
+ 80 |
23 |
|
− 30 |
24 |
|
= −151, 6 кН м3 . |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
6 |
|
|
|
|
6 |
6 |
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|||||||||||||
4. Составляем уравнение жесткости |
|
|
|
|||||||||||||||||||||||||||||||||
откуда |
|
|
|
|
|
|
|
|
y |
|
|
x =6 |
|
= |
|
EIy |
|
x =6 |
|
≤ [ y]= |
0,01 м, |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
I ≥ |
|
EIy |
|
x=6 |
|
= |
|
|
151, 6 103 |
|
= |
|
7,58 10−5 м4= |
7580 см4 . |
||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
E 0, 01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
2 1011 0, 01 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Из таблиц сортаментов этому моменту инерции соответствует:
а) двутавр 1 № 30а (I = 7780 см4 ;W = 518 см3 ; F = 49,9 см2 )
KI = W = 10,38 см;
F
б) швеллер1 № 33 (I = 7980 см4 ;W = 484 см3 ; F = 46,5 см2 )
KI = W = 10, 41 см.
F
Следовательно, в качестве сечения балки выбираем швеллер № 33.
Задание 4.1
Из расчета на жесткость методом начальных парамет-
ров выбрать по таблицам сортаментов |
(ГОСТ 8239-89 и |
ГОСТ 8240-89), используя коэффициент |
качества, сечение |
стальной ( E = 2 105 МПа) балки, нагруженной так, как показано на рис. 4.2, если прогиб балки на расстоянии x = 5 м от левого конца не должен превышать 1 см.
52

Содержание работы:
1.Найти реакции опор и проверить правильность их определения.
2.Записать:
а) приближенное дифференциальное уравнение изогнутой оси балки;
б) уравнения углов поворота сечения балки с неизвестным параметром;
в) уравнение упругой линии (прогибов) балки с двумя неизвестными параметрами.
3.Используя граничные условия, определить неизвестные начальные параметры.
4.Записать универсальное уравнение упругой линии балки и вычислить прогиб при x = 5 м.
5.Из условия жесткости определить допустимую величину момента инерции сечения стальной балки.
6.По коэффициенту качества из таблиц сортаментов выбрать сечение балки.
Указание
Числовые данные и виды схем выбираются в соответствии
сшифром по табл. 4.1 и рис. 4.2.
Таблица 4.1
Номер |
|
|
|
Цифра шифра |
|
|
|
||
1-я |
|
2-я |
|
3-я |
|
4-я |
5-я |
6-я |
|
|
Схема |
а1, м |
а2, м |
а3, м |
Р, т |
|
М, тм |
q1, т/м |
q2, т/м |
1 |
1 |
2 |
1,5 |
3 |
2 |
|
4 |
2 |
3 |
2 |
2 |
1,5 |
2,5 |
3,5 |
1,5 |
|
3 |
3 |
2 |
3 |
3 |
1,5 |
2 |
3 |
3 |
|
4 |
2 |
0 |
4 |
4 |
2 |
1,5 |
2,5 |
2 |
|
3 |
1 |
0 |
5 |
5 |
1 |
1 |
4,5 |
4 |
|
4 |
2 |
0 |
6 |
6 |
2 |
1,5 |
3 |
3 |
|
1 |
1,5 |
0 |
7 |
7 |
0,5 |
1 |
4 |
4 |
|
1 |
2 |
3 |
8 |
8 |
0,5 |
2 |
3,5 |
4 |
|
2 |
3 |
0 |
9 |
9 |
1 |
1,5 |
4 |
1 |
|
4 |
2 |
0 |
10 |
10 |
1,5 |
2 |
4,5 |
2 |
|
4 |
2 |
0 |
53
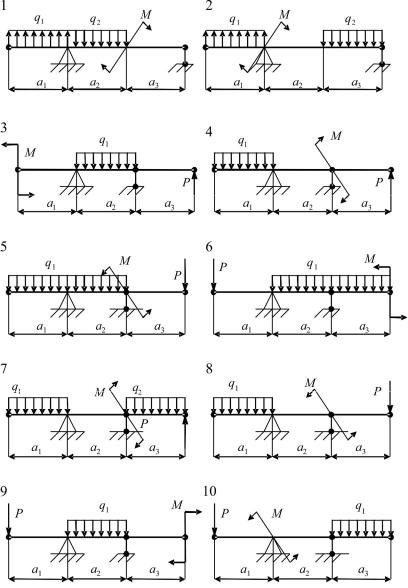
Рис. 4.2
54
Вопросы для самопроверки
1.Что называется изогнутой осью балки?
2.Какие величины характеризуют перемещение произвольного сечения балки?
3.Что называется прогибом и углом поворота?
4.Как записывается дифференциальное уравнение упругой линии?
5.Основные правила метода начальных параметров при определении перемещений балки?
6.Что представляют собой уравнения метода начальных параметров и почему они так называются?
7.Как определяются значения неизвестных начальных параметров для различных случаев закрепления балок?
8.Основные правила построения и контроля эпюр углов поворота и прогибов сечений балки?
9.Как определяются деформации методом непосредственного интегрирования?
ТЕМА 5. НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ. КРИТЕРИЙ МОРА
Под напряжённым состоянием в точке понимают совокупность напряжений на всех площадках, проходящих через заданную точку. Каким бы ни было напряженное состояние в точке, всегда существуют три взаимно перпендикулярных площадки, на которых касательные напряжения равны нулю, а нормальные напряжения имеют стационарные значения. Эти площадки называются главными. Нормальные напряжения, действующие на главных площадках, называются главныминапряжениями.
В зависимости от того, сколько главных напряжений действует в окрестности точки, различают три вида напряженного состояния:
55
1)линейное (одноосное) – если одно главное напряжение отлично от нуля, а два других равны нулю;
2)плоское (двухосное) – если два главных напряжения отличны от нуля, а одно равно нулю;
3)объемное (трехосное) – если все три главных напряжения отличны от нуля.
Линейное напряженное состояние встречается при растя- жении-сжатии, плоское напряженное состояние встречается при изгибе и кручении.
Правило знаков для определения нормальных и касательных напряжений, действующих на элемент: нормальные напряжения считаются положительными, растягивающие элемент; касательные напряжения считаются положительными, вращающие элемент по часовой стрелке.
Деформированное состояние в точке обладает свойствами, аналогичными свойствам напряженного состояния. Совокупность деформаций, возникающих по разным осям и в различных плоскостях, проходящих через данную точку, определяет деформированное состояние в рассматриваемой точке. Существуют три взаимно перпендикулярных направления, по которым волокна или удлиняются, или укорачиваются. Они называются главными осями деформаций. Деформации в направлении главных осей называются главными деформациями.
Задачи, рассматриваемые в теории напряженного состояния, могут быть представлены в прямой и обратной постановке:
а) прямая задача – в точке известны положения главных площадок и соответствующие им главные напряжения; требуется найти нормальные и касательные напряжения по площадкам, наклоненным под заданным углом α к главным;
б) обратная задача – в точке известны нормальные и касательные напряжения, действующие по двум взаимно перпендикулярным произвольным площадкам, проходящим через данную точку; требуется найти направление главных площадок и главные напряжения.
56

Основные критериальные гипотезы теории предельных состояний
1.Критерий наибольших нормальных напряжений [первая (I) теория прочности]: σэквI ≤ [σ] , где σэкв – эквивалентное напряжение, под действием которого материал в условиях простого растяжения-сжатия оказывается в равноопасном состоянии с рассматриваемым сложным напряженным состоянием.
2.Критерий наибольших линейных деформаций [вторая
(II)теория прочности]: εэквII = σ1 − µ(σ2 + σ3 ) ≤ [σ], где σ1 , σ2 , σ3 – главные напряжения; µ – коэффициент Пуассона.
3.Критерий наибольших касательных напряжений [третья
(III)теория прочности]: σэквIII = σ1 − σ3 ≤ [σ] .
4.Критерий удельной потенциальной энергии формоиз-
менения [четвертая (IV) теория прочности]
|
σэквIV = |
1 |
[(σ1 − σ2 )2 + (σ2 − σ3 )2 + (σ3 − σ1 )2 ] ≤ [σ] . |
|||
|
|
|||||
|
2 |
|
|
|
|
|
|
5. Критерий Мора |
(V теория прочности): σэквМ = |
||||
= σ1 |
− k σ3 ≤ [σ] , где k = |
[σ]р |
|
– отношение предельных напря- |
||
[σ]c |
|
|||||
|
|
|
|
|
|
|
жений при одноосном растяжении и при одноосном сжатии. Аналитически исследовать напряженное состояние в точке
нагруженного тела можно с помощью формул или при графическом исследовании плоского напряженного состояния с помощью кругов напряжений Мора. Круги Мора, построенные по всем трем главным напряжениям в точке, упрощают анализ объемного напряженного состояния.
На основании теории предельного состояния может быть осуществлена так называемая полная проверка прочности балки при поперечном изгибе, которая, кроме нормальных и касательных напряжений в поперечных сечениях балки, учитывает также и влияние главных напряжений.
57
Пример 5.1
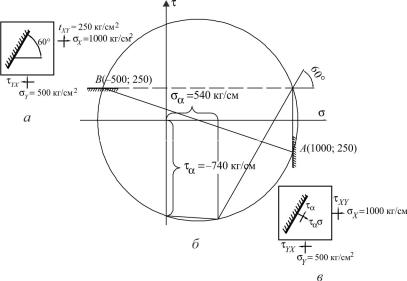
В опасной точке упругодеформированной конструкции выделен элемент (рис. 5.1, а), по грани которого действуют нормальные и касательные напряжения. Требуется исследовать напряженное и деформированное состояние в опасной точке по приведенной схеме.
Решение:
1. Построим круг Мора для заданного напряженного состояния. Для этого проведем прямоугольную систему координат σ, τ (рис. 5.1, б). Нанесем на ней точку A, абсцисса которой равна (при некотором масштабе) нормальному напряжению σx ,
а ордината – касательному напряжению τxy . Напряжение σx
положительно, поэтому оно отложено вправо от оси ординат; напряжение τxy отрицательно и отложено вниз от оси абсцисс.
Затем нанесем на график точку B с отрицательной абсциссой σy
Рис. 5.1
58
и положительной ординатой τxy . Величина τxy в условии задачи
не дана, но мы знаем, что согласно закону парности касательных напряжений касательное напряжение τxy по абсолютной вели-
чине равно касательному напряжению τxy .
Точки A и B соединяем прямой AB и на ней как на диаметре строим круг Мора. Центр круга Мора лежит на пересечении прямой AB с осью абцисс (осью σ).
Точка A (1000; –250) характеризует напряженное состояние на вертикальной плоскости, проведенной через точку, в которой исследуется напряженное состояние, а точка B (–500; 250) – напряженное состояние по горизонтальной плоскости. В соответствии с этим проведем через точку A вертикальную линию, изображающую вертикальную плоскость, а через точку B – горизонтальную линию, изображающую горизонтальную плоскость. Точка пересечения этих линий, лежащая на круге Мора, называется полюсом.
Полюс обладает следующим замечательным свойством: направление любой площадки, проведенной через точку круга Мора, которая характеризует напряженное состояние на этой площадке, обязательно проходит через полюс C.
Поэтому, для того чтобы найти напряжения σα, τα, дейст-
вующие в указанном сечении, необходимо из полюса C провести прямую, параллельную этому сечению, до пересечения с кругом Мора.
Абсцисса точки пересечения равна (в принятом масштабе) нормальному напряжению σα = 540 кг / см2 , а ордината – касательному напряжению τα = −740 кг / см2 в заданном сечении.
Направление найденных напряжений показано на рис. 5.1, в.
2. Для определения величины главных напряжений необходимо найти точки пересечения круга Мора с осью σ, то есть точки, координаты τ которых равны нулю. Для заданного напряженного состояния это две точки: одна с абсциссой, равной
59
напряжению 1040 кг / см2 , другая с абсциссой, равной напряже-
нию −540 кг / см2 .
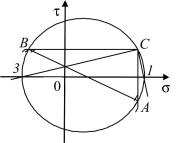
Поскольку мы исследуем плоское напряженное состояние, при котором одно из главных напряжений равно нулю, а в общем случае главные напряжения связаны между собой неравенством σ1 ≥ σ2≥ σ3 , то приходим к выводу, что левая точка пересечения круга Мора с осью абсцисс определяет главное напряжение σ3 = −540 кг / см2 и может быть обозначено индексом 3, а правая точка пересечения круга Мора с осью σ определяет главное напряжение σ1 = 1040 кг / см2 и может быть обозначена индексом 1 (рис. 5.2).
Рис. 5.2
Для определения направлений сечений, в которых действуют главные напряжения σ1 и σ3 , необходимо точки 1 и 3 по-
следовательно соединить прямыми с полюсом C. Искомые направления главных площадок-сечений параллельны соответствующим прямым.
3. Для определения величины максимальных и минимальных касательных напряжений необходимо через центр круга Мора провести вертикальную прямую (рис. 5.3). Ордината точки пересечения этой прямой с верхней частью круга Мора даст величину максимального касательного напряжения. Для задан-
60
