
02 Основы работы в MATLAB
.pdf
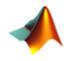
Функции для округления чисел
11
Функции для операции с комплексными числами
Целочисленные |
Описание функции |
Функции |
|
|
|
real(z) |
выдает действительную часть комплексного аргумента z |
|
|
imag(z) |
выдает мнимую часть комплексного аргумента z |
|
|
angle(z) |
выдает значение аргумента комплексного числа z в |
|
радианах от -π до +π |
|
|
conj(z) |
выдает число, комплексного сопряжение z |
|
|
>> a=2+2i; b=-3i; |
>> z=-5+3i; |
|
|
>> real(z) |
|
|
|
|
|
|
|
>> a+b |
ans = |
|
|
-5 |
|
|
|
ans = |
|
|
|
>> angle(z) |
|
|
|
2.0000 - 1.0000i |
|
|
|
ans = |
|
|
|
|
|
|
|
>> (a+b)^2 |
2.6012 |
(в радиане) |
|
>> ans*180/pi |
|
||
ans = |
|
||
ans = |
|
|
|
3.0000 - 4.0000i |
|
|
|
149.0362 |
(в градусе) |
|
|
|
12 |
||
Как создать специальные функции в среде MATLAB ?
Кроме стандартных встроенных функций, Matlab позволяет пользователям создать специальные функции.
New M-file (or M-function)
М-файлы готовляются в виде;
1.М-file (окна редактирования для составления программ или записи ряд команд для многократного использования)
2.М-function (создается с заголовком, в котором можно указать выходные и входные параметры функции )
М-Функция, как правило, предназначена для неоднократного использования, заголовок ее имеет вид:
function [name1, name2, ….] = functionname(var1, var2, var3,…..)
где;
name1, name2 − список выходных, которые вычисляются через var1, var2,var3,....
fun − имя функции или М-файла
var1, var2,var3, ….. − входные параметры. |
13 |
|
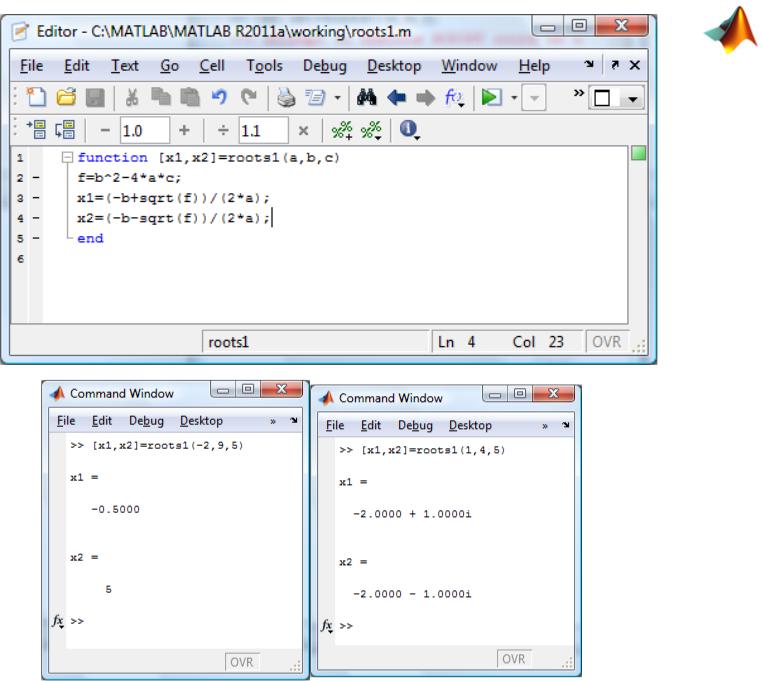
Пример 1.
14

Пример 2
function [area volume] =cylinder(radius, length)
volume=pi*radius^2*length;
area = 2 * pi * length + 2.* pi *r *r;
end
Как запускать функцию ? Пишите заголовок функции в командном окне MATLAB с значениями входных параметров,
>> [area volume] = cylinder(2,10) area =
150.7964
volume=
125.6637
15
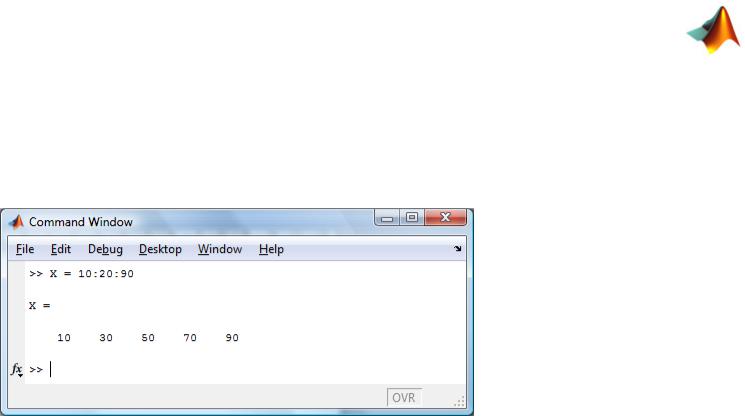
2.3. Векторы, поэлементные и матричные операции, вычисление сложных функции от данного вектора
Способы создания одномерных массивов (векторов)
1.name = Xn : шаг : Xk
x [Xn,Xk], Xn обозначает начальное значение интервала, а Хk конечное значение.
16
2. |
name = [x1 x2 x3 x4 x5] |
или |
name = [x1, x2, x3, x4, x5] |
|||
|
>> x= [10 |
20 |
30 |
40 |
50 |
60] |
|
x= |
|
|
|
|
|
|
10 |
20 |
30 |
40 |
50 |
60 |
3.С помощью встроенной функции linspace,
name = linspace(Xn , Xk, n), n - количество точек в интервале
>>x=linspace(1, 10, 10) x=
1 2 3 4 5 6 7 8 9 10
4.С помощью оператора цикла for
>>x= for i=1:10 x(i) = i end x=
1 2 3 4 5 6 7 8 9 10
17
МАТРИЦЫ как двумерные массивы
A = [A11, A12, A13; A21, A22, A23; A31, A32, A33]
или A = [A11 A12 A13; A21 A22 A23; A31 A32 A33]
>> B = [1 |
2 3; 4 5 6; 7 8 9] |
|
B = |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
>> A2(1,3)*B(3,1)
ans =
21
18
Операции с массивами в Matlab
Матричные и поэлементные операции
A и B две массивы (вектор или матриц)
A+B |
− сложение двух матриц одной размерности |
A - B |
− вычитание матриц одной размерности |
A * B |
− умнажение матриц соответствующего размера С(i,j) = A(i,k)*B(k,j) |
A .* B |
− поэлементное умножение двух матриц |
A / B |
− деление матриц слева направа |
A ./ B − поэлементное прямое деление, А на В |
|
A \ B |
− деление матриц справа налево |
A . \ B − поэлементное обратное деление, В на А |
|
A ^ B |
− возведение матрицы А в степень матрицы В, В может быть В(1,1)= а |
A .^ B − поэлементное возведение матрицы А в степень матрицы В |
|
A' |
− транспонирование от А |
|
19 |
Матричные и поэлементные операции:
матричные: производят действия по правилам матричной алгебры
поэлементные: производят действия над соответствующими элементами матриц
•размеры матриц должны быть одинаковыми
•от матричных операций отличаются точкой перед знаком операции
20
