
Гизатуллин монография 1
.pdf
мощью контуров К4 и К5 (рис. 3.16); 2) измерение электромагнитной помехи в контуре К1 внутри тестового корпуса СВТ (рис. 3.17); 3) измерение электромагнитной помехи в контуре К3 внутри корпуса персонального компьютера (рис. 3.17).
Рис. 3.15. Генератор импульсного тока (ИГМ 4.1)
Ток разряда молнии при всех экспериментальных исследованиях соответствует следующим параметрам (ГОСТ 50649-94): фронт – 6,4 мкс; спад на уровне 50 % – 16 мкс; амплитуда до 1,6 кА (напряженность магнитного поля создаваемого индукционной катушкой до 1,4 кА/м).
а |
б |
Рис. 3.16. Стенд для измерения магнитного поля на контурах К4, К5:
а – схема; б – фотография; 1 – индукционная катушка; 2 – контура (К4, К5); 3 – изоляционная подставка; 4 – изоляционные фиксаторы индукционной катушки;
ГИТ – генератор импульсного тока
161
а |
б |
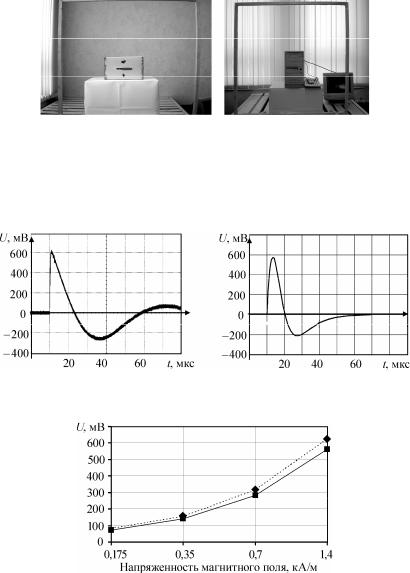
Рис. 3.17. Стенд для измерения электромагнитных помех в контурах К1 (а), К3 и анализу устойчивости СВТ к воздействию импульсного магнитного поля разряда молнии (б)
1. Измерение электромагнитных помех в контурах К4 и К5 (рис. 3.18 – 3.21). Максимальная напряженность импульсного магнитного поля – 1,4 кА/м.
а |
б |
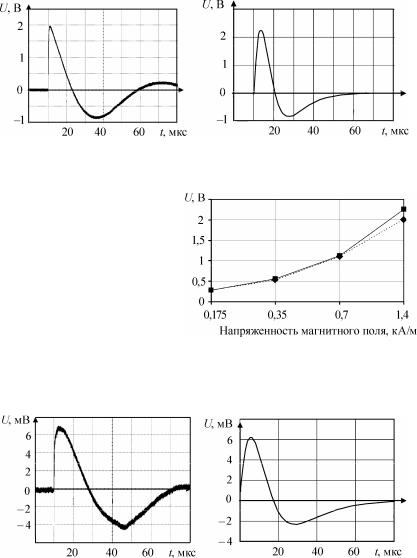
Рис. 3.18. Электромагнитная помеха в контуре К4:
а – эксперимент; б – моделирование
Рис. 3.19. Зависимость напряжения электромагнитной помехи в контуре К4 от напряженности импульсного магнитного поля разряда молнии:
 – моделирование;
– моделирование;  – эксперимент
– эксперимент
162
а |
б |
Рис. 3.20. Электромагнитная помеха в контуре К5:
а – эксперимент; б – моделирование
Рис. 3.21. Зависимость напряжения электромагнитной помехи в контуре К5 от напряженности импульсного магнитного поля разряда молнии
2. Измерение электромагнитных помех в контуре К1, внутри тестового корпуса СВТ при воздействии импульсного магнитного поля разряда молнии (рис. 3.22 – 3.27). Максимальная напряженность магнитного поля – 1,4 кА/м.
а |
б |
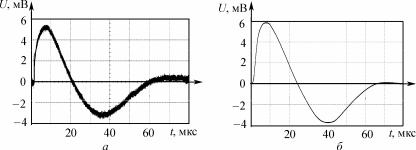
Рис. 3.22. Электромагнитная помеха в контуре К1: |
|
а – эксперимент; б – |
моделирование; площадь отверстия – 250 мм2; |
вектор напряженности магнитного поля перпендикулярен плоскости отверстия
163
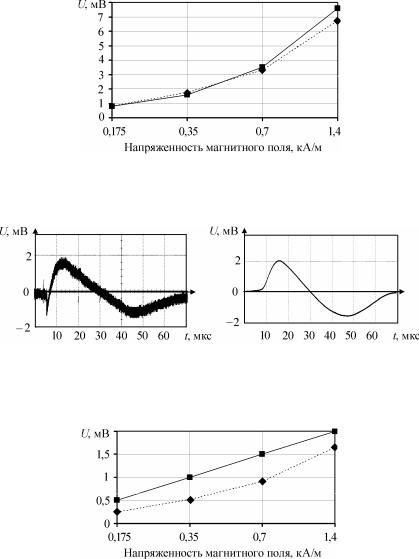
Рис. 3.23. Зависимость напряжения электромагнитной помехи в контуре К1 тестового корпуса от напряженности магнитного поля разряда молнии:
 – моделирование;
– моделирование;  – эксперимент
– эксперимент
а |
б |
Рис. 3.24. Электромагнитная помеха в контуре К1:
а – эксперимент; б – моделирование; площадь отверстия – 250 мм2; вектор напряженности параллельно плоскости отверстия
Рис. 3.25. Зависимость напряжения электромагнитной помехи в контуре К1 от напряженности магнитного поля разряда молнии:
 – моделирование;
– моделирование;  – эксперимент
– эксперимент
164
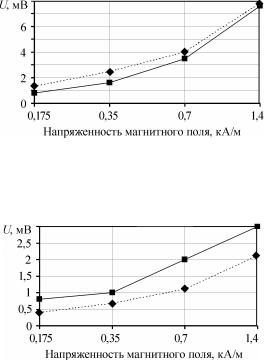
Рис. 3.26. Зависимость напряжения электромагнитной помехи в контуре К1 тестового корпуса от напряженности магнитного поля разряда молнии (площадь отверстия – 500 мм2; вектор напряженности перпендикулярен плоскости отверстия):  – моделирование;
– моделирование;  – эксперимент
– эксперимент
Рис. 3.27. Зависимость напряжения электромагнитной помехи в контуре К1 тестового корпуса от напряженности магнитного поля разряда молнии (площадь отверстия – 500 мм2; вектор напряженности параллельно плоскости отверстия):
 – моделирование;
– моделирование;  – эксперимент
– эксперимент
Для полноценного анализа электромагнитных помех в лини-
ях связи СВТ при воздействии импульсного магнитного поля раз-
ряда молнии проведена статистическая обработка и анализ экспе-
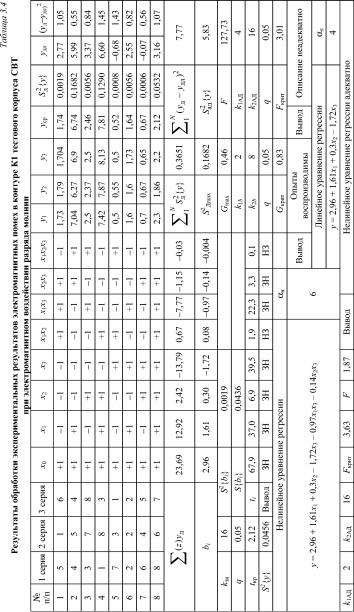
риментальных данных. Для обработки результатов использована схема полнофакторного эксперимента [293] с тремя сериями испы-
таний (табл. 3.4).
Выходной фактор: y – напряжение (максимальное) электро-
магнитной помехи в исследуемом контуре К1, В.
165
166
Входные факторы: X1 – максимальная напряженность импульсного магнитного поля разряда молнии, А/м; X2 – площадь отверстия на передней панели исследуемого корпуса, мм2; X3 – ориентация тестового корпуса по отношению к вектору напряженности магнитного поля.
Интервал варьирования факторов: X1 – 0,7 кА/м (–1), 1,4 кА/м (+1); X2 – 250 мм2 (–1), 500 мм2 (+1); X3 – вектор напряженности импульсного магнитного поля перпендикулярно плоскости отверстия на передней панели тестового корпуса СВТ (–1), вектор напряженности импульсного магнитного поля параллельно плоскости отверстия на передней панели тестового корпуса (+1).
Таким образом, нелинейное уравнение регрессии выглядит следующим образом:
y = 2,96 + 1,61*X1 + 0,3*X2 – 1,72*X3 –
–0,97*X1*X3 – 0,14*X2*X3.
3.Измерение электромагнитной помехи в контуре внутри
корпуса персонального компьютера (рис. 3.28).
Рис. 3.28. Электромагнитная помеха в контуре К3 внутри корпуса персонального компьютера: а – эксперимент; б – моделирование; максимальная напряженность – 0,7 кА/м; вектор напряженности параллельно длинной стороне корпуса
Табл. 3.5 содержит результаты экспериментальных исследований помехоустойчивости персонального компьютера при воздействии импульсного магнитного поля разряда молнии.
167
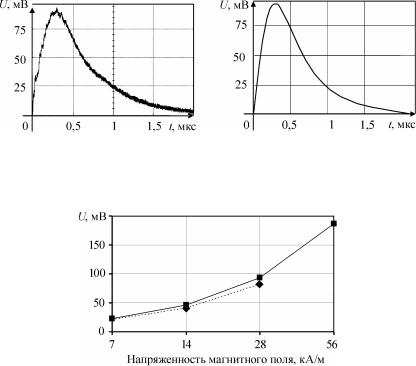
Таблица 3.5
Экспериментальные исследование помехоустойчивости персонального компьютера при воздействии импульсного магнитного поля разряда молнии (количество воздействий для каждого варианта – 10 раз)
Напряженность |
Ориентация корпуса по отношению |
|
магнитного поля, |
к вектору магнитного поля |
Количество сбоев |
кА/м |
(по отношению к передней панели) |
|
0,175; 0,35; 0,7; 1,4 |
Перпендикулярно, параллельно |
0 |
4. Измерение электромагнитных помех в контурах К4 и К5 при воздействии импульсного магнитного поля (фронт 1,05 мкс,
спад 50 % 45 мкс) (рис. 3.29 – 3.31).
а |
б |
Рис. 3.29. Электромагнитная помеха в контуре К4:
а – эксперимент; б – моделирование; максимальная напряженность импульсного магнитного поля – 28 А/м
Рис. 3.30. Зависимость напряжения электромагнитной помехи в контуре К4 от напряженности импульсного магнитного поля разряда молнии:
 – моделирование;
– моделирование;  – эксперимент
– эксперимент
168
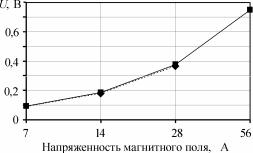
Рис. 3.31. Зависимость напряжения электромагнитной помехи в контуре К5 от напряженности импульсного магнитного поля разряда молнии:
 – моделирование;
– моделирование;  – эксперимент
– эксперимент
3.4. Исследование магнитных полей внутри здания при воздействии разряда молнии на основе теории масштабного эксперимента
Для анализа магнитных полей внутри зданий при воздействии разряда молнии на систему молниезащиты здания разработана методика на основе теории масштабного эксперимента. Необходимость методики обоснована тем, что при изучении электромагнитных процессов, протекающих в различных системах здания, СВТ или других объектов исследования, возникают трудности с изготовлением макетов, имитаторов поля в полном масштабе или измерением быстротекущих процессов. В данном случае выходом является использование макетов или имитаторов, чьи размеры, материал и временные характеристики приемлемы для экспериментатора. Задача сводится к выделению критерия подобия протекания электромагнитных процессов на макрообъектах с различными электромагнитными характеристиками, с предположением, что электромагнитные процессы на оригинале и модели описываются феноменологическими уравнениями Максвелла [291, 292].
169

В [292] приведен вывод соотношения коэффициентов подобия для подбора параметров масштабной модели:
f = a |
|
; a = |
1 |
|
k |
; |
с = |
|
1 |
, |
|
km |
|||||||||||
|
|
|
|
||||||||
|
|
|
p m |
|
|
km |
|||||
где a – коэффициент масштабирования геометрических размеров; f – коэффициент масштабирования временной орты; k – коэффициент масштабирования электрической характеристики материала (ε – диэлектрическая проницаемость); m – коэффициент масштабирования магнитной характеристики материала (μ – магнитная проницаемость); p – коэффициент масштабирования электрической характеристики материала (σ – проводимость); c – коэффициент масштабирования скоростей. Если допустить с = 1, т.е. средняя скорость движения носителей в оригинале и модели одинаково в подобных точках, то приходим к соотношениям:
f = a; k = 1 ; apm = 1. m
Если учитывать, что обычно коэффициенты k = m = 1, так как в реальных условиях проведения масштабного эксперимента практически нельзя подобрать материалы с определенными, сильно отличающимися от оригинала диэлектрическими и магнитными свойствами. Таким образом, получаем следующие выражения:
f = a; a = 1 . p
Как видим, изменение коэффициента масштабирования временной орты f приводит к пропорциональному изменению коэффициента масштабирования физических размеров оригинала и модели a. При этом коэффициент масштабирования электрической проводимости материала p должен измениться обратно пропорционально данным коэффициентам. Трудности, связанные с масштабированием активного сопротивления теоретически можно преодолеть, если заменить материалы оригинала другим материа-
170
