
Гизатуллин монография 1
.pdf
4. Соотношение полной длины проводников неэкранирован-
ной витой пары LZ к величине шага скрутки намного больше единицы ( LZ 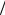 p >> 1).
p >> 1).
5.Электромагнитное поле рассматривается как плоская электромагнитная волна, воздействующая на неэкранированную витую пару одновременно по всей длине.
6.Не учитывается расположение неэкранированной витой пары относительно корпусов и экранирующих поверхностей [264, 265].
7.Не рассматривается фантомная цепь, которая представляет собой дополнительный путь связи и сигналы, передаваемые от источников по основным цепям и данным цепям, можно рассматривать отдельно.
Следующим шагом, в решении данной задачи является введение нагрузочных цепей в линии передачи витой пары. Предполагаем, что полная длины обоих проводников витой пары равняется L.
Собственно, длина самой витой пары с учетом скрутки при этом
составит LZ |
= |
paL |
. На концах линии передачи установлены на- |
|
2 × p |
||||
|
|
|
грузки ZS и ZL, соответственно, при l = 0 и l = L. Данная конфигурация линии передачи представлена на рис. 2.44 [257].
Рис. 2.44. Конфигурация неэкранированной витой пары с установленными нагрузочными цепями
В данном случае токи на нагрузках I (0) и I (L) , соответст-
венно, при l = 0 и l = L можно рассчитать с помощью следующих уравнений:
121

|
|
|
|
|
|
|
1 |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
Z |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
I (0) = |
|
|
cosh(g(L - l)) + |
|
|
|
sinh(g(L - l)) ´× |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
D |
∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
ZC |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
uri |
|
|
|
|
|
|
|
|
|
|
|
|
uri |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
´ E (x1, y1, z1 ) × l1(l) - E ( x2 , y2 , z2 ) × l2 (l) dl |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 b(l ) |
uri |
|
|
r |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Z |
L |
|
|
|
|
|
|
|
|
|
b(l ) uri |
r |
|
||||||
- |
|
∫ |
E (r,l) × dr |
l=L |
+ |
|
|
|
cosh(g × L) + |
|
|
sinh(g × L) |
∫ |
E (r,l) ×dr |
l=0 . |
|||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
D a(l ) |
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
ZC |
|
|
|
|
|
|
|
|
a(l ) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
L |
|
|
|
|
|
|
|
Z |
S |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
I (L) = |
|
|
|
|
|
cosh(g × l) + |
|
|
|
sinh(gl) ´ |
|
(2.21) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
D |
∫0 |
|
|
|
|
|
|
|
ZC |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
uri |
(x1, y1, z1 )× l1 |
|
|
uri |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
´ E |
(l) - E |
(x2 , y2 , z2 )× l2 (l) dl - |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Z |
S |
|
|
|
|
|
|
|
b(l ) uri |
|
|
|
|
r |
|
|
|
||||||
|
|
|
- |
|
|
cosh(g × L) + |
|
|
|
sinh(g × L) × |
∫ E (r,l) |
× d r |
l=L |
+ |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
D |
|
|
|
|
|
|
|
|
ZC |
|
|
|
|
|
|
|
a(l ) |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
b(l ) ur |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
∫ |
Ei (r,l) × dr |
|
l=0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a(l ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
S |
Z |
L |
|
|
|
|
|
||
где D = cosh(g × L)(ZS + Z L ) + sinh(g × L) ZC + |
|
|
|
; |
|
|
|
|||||||||||||||||||||||||||||||
ZC |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ZC = 
 (Zi + j ×w× Le ) /(G + j ×w×C) , g =
(Zi + j ×w× Le ) /(G + j ×w×C) , g = 
 (Zi + j ×w× Le ) ×(G + j ×w×C) ;
(Zi + j ×w× Le ) ×(G + j ×w×C) ;
Zi = |
2 × Rs |
; |
Rs = |
1 |
; d0 = |
|
|
2 |
|
|
; |
G = 2 × p×C × tan d, |
|
s× d0 |
|
× p× f ×m × s |
|||||||||
|
p× d |
|
2 |
|
|
|
||||||
где ω, λ – |
угловая частота и длина волны воздействующего элек- |
|||||||||||
тромагнитного поля, |
соответственно; |
μ – |
относительная магнит- |
|||||||||
ная проницаемость изоляции линий передачи; d0 – толщина скин-
122

слоя проводника; σ – проводимость линии передачи на единицу длины; d – диаметр цилиндрических проводников витой пары; tan δ – тангенс угла потерь изоляции линий передачи.
Действительные напряжения на нагрузках Vd (0) и Vd (L)
вычисляются соответственно:
Vd |
(0) = |
|
|
V (0) |
|
|
= |
|
|
I (0) |
× |
ZS |
|
|
; |
Vd |
(L) = |
|
|
V ( |
L |
) |
|
|
= |
|
|
I (L) × |
ZL |
|
|
, |
|||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
где соответственно, V (0) и V (L) расчетные комплексные напря-
жения на нагрузках ZS и ZL.
Уравнения (2.21) учитывают воздействующее электромагнитное поле в общем виде, т.е. оно может быть и не неоднородной. Однако, для оценки влияния электромагнитного поля на линию передачи в виде витой пары, ограничимся случаем дальней области, т.е. электромагнитное поле рассматривается в виде плоской волны распространяющееся в свободном пространстве. В данном случае воздействующее электромагнитное поле описывается следующим образом:
uri |
+ ey ay |
+ ez az )e− j(kx x+k y y+kz z); |
E ( x, y, z) = Ei (ex ax |
ex = sin(qE )sin(qp ); ey = -sin(qE ) cos(qp )cos(fp ) - cos(qE )sin(fp );
ez = -sin(qE )cos(qp )sin(fp ) + cos(qE )cos(fp ); |
(2.22) |
kx = -k cos(qp ) ; k y = -k sin(qp )cos(fp ); kz = -k sin(qp )sin(fp ) ;
k= w = 2 × p , c0 l
где c0 – скорость света; qp , fp , qE – углы падения и поляризации воздействующего электромагнитного поля по отношению к линии
123

передачи. Таким образом, подставляя уравнение (2.22) в уравнения (2.21) и учитывая, что минимальная длина волны воздействующего электромагнитного поля намного больше ( λ >> s ) расстояния между проводниками витой пары и выполняется соотношение
LZ >> 1, получаем более простые уравнения для решения задачи p
электромагнитного воздействия на неэкранированную витую пару:
|
Ei s |
|
|
|
Z |
L |
|
|
|
I (0) » - |
|
|
(a × ex |
+ j × k y |
× ez ) F+ (L) + |
|
F- (L) |
- |
|
2 |
|
Z C |
|||||||
|
× D |
|
|
|
|
||||
|
|
|
Z |
L |
|
|
|
|
|
|
-(aey |
- j × kx ez ) K+ (L) + |
|
|
K- (L) |
+ 2(ex cos(a × L) + |
|||||
|
ZC |
|||||||||
|
|
|
|
|
|
|
|
|||
+ey sin(a × L))e- jkz L - 2 × ex |
|
|
|
|
Z |
L |
|
|||
cosh(g × L) + |
|
sinh(g × L) ; (2.23) |
||||||||
ZC |
||||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
Ei s |
|
|
|
|
|
Z |
S |
|
|
|
|
||||
|
I (0) » - |
|
|
|
(a × ex + j × k y × ez ) F+* (L) |
+ |
|
|
F-* (L) |
- |
|||||||||
|
2 |
|
Z C |
|
|||||||||||||||
|
|
|
× D |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Z |
S |
|
|
|
|
|
|
|
|
|
|
|
-(aey - j × kx × ez ) K+* (L) + |
|
K-* (L) |
+ |
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
ZC |
|
|
|
|
|
|
|
|
|||
|
|
Z |
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+2 cosh(g × L) + |
|
|
sinh(g × L) (ex |
cos(a× L) + ey sin(a× L))e- jkz L - 2 × ex , |
|||||||||||||||
ZC |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F± (L) = F1 (L) ± F2 (L); |
K± (L) = K1 (L) ± K2 (L); |
|
|
|
||||||||||||||
F * (L) = ±F (L)e- g×L + F (L)eg×L ; K * (L) = ±K |
(L)e- g×L + K |
2 |
(L)eg×L ; |
||||||||||||||||
± |
1 |
|
|
|
2 |
± |
|
1 |
|
|
|
|
|
|
|
||||
124
|
|
|
F (L) = |
a × eg×L |
- (acos(a × L) + (g + j × kz )sin(a × L))e- j×kz ×L |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
||||
|
|
|
|
|
|
(g + |
j × kz )2 + a2 |
|
|
||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
F (L) = |
a × e-g×L |
- (acos(a × L) + (-g + j × kz )sin(a × L))e- j×kz ×L |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
||||
|
|
|
|
|
|
|
(g - |
j × kz )2 + a2 |
|
|
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
(L) = |
(g + j × kz )eg×L + (a ×sin(a × L) - (g + j × kz ) cos(a × L))e- jkz L |
|||||||||||||||
K |
|
|
|
|
|
|
|
|
|
|
|
; |
|
||||||
|
|
|
|
|
(g + |
j × kz )2 + a2 |
|
|
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
(L) = |
(-g + j × kz )e- g×L + (a ×sin(a × L) + (g - j × kz )cos(a × L))e- jkz L |
||||||||||||||||
K |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||
|
|
|
|
|
|
(g - |
j × kz )2 + a2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
kx = |
kx a× p |
; k y = |
k y a × p |
; kz = |
kz a × p |
. |
|
|
|
|
|||
|
|
|
|
|
|
2 × p |
|
2 × p |
2 × p |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Мощность рассеивания P на нагрузках ZS, ZL неэкранированной витой пары может быть вычислена с помощью следующих выражений:
PS |
= |
1 |
Re(ZS × |
|
I (0) |
|
2 ); |
PL |
= |
1 |
Re(ZL × |
|
I (L) |
|
2 ). |
(2.24) |
|
|
|
|
|
||||||||||||||
|
|
||||||||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
Таким образом, представленные аналитические выражения используются для моделирования электромагнитных помех в неэкранированной витой паре при широкополосных электромагнитных воздействиях. Но аналитический подход, рассмотренный в данном разделе, имеет ряд существенных ограничений и допущений, что сильно ограничивает его применение на практике и служить для быстрой оценки электромагнитных помех в неэкранированной витой паре при широкополосных электромагнитных воздействиях. В связи с этим, для анализа электромагнитных помех в неэкранированной витой паре при внешних широкополосных электромагнитных воздействиях, реализованы имитационные модели. Напри-
125
мер, на рис. 2.45 представлен пример имитационной модели для анализа электромагнитных помех в неэкранированной витой паре 5 категории.
а |
б |
Рис. 2.45. Имитационная модель неэкранированной витой пары для анализа электромагнитных помех при широкополосных электромагнитных воздействиях:
а – графическое представление; б – метод подсеток; программа Microwave Studio
Преимущества имитационных моделей: точное воспроизведение конструкции неэкранированной витой пары (8 проводников); произвольная ориентация векторов воздействующего ЭМИ; произвольная нагрузка; анализ до сверхвысоких частот; возможность учета расположения неэкранированной витой пары относительно корпусов, третьих цепей (цепи питания, трубопроводы и т.п.) и экранирующих поверхностей.
2.8.Прогнозирование электромагнитных помех
влиниях связи средств вычислительной техники при широкополосных электромагнитных воздействиях
Для прогнозирования электромагнитных помех в проводных линиях связи современных СВТ внутри зданий и сравнения полученных результатов моделирования с экспериментальными результатами других авторов при широкополосных электромагнитных воздействиях приводится ряд практических примеров. Все
126
данные примеры имеют общую направленность и позволяют судить об области адекватности предложенных ранее аналитических и имитационных моделей. Примеры 1 и 2 содержат результаты сравнения электромагнитных помех в линиях связи СВТ при воздействии ЭСР, полученные с применением предложенных имитационных моделей, и результатов экспериментальных исследований других авторов. При этом рассматриваются различные, наиболее вероятные и опасные механизмы воздействия ЭСР. Пример 3 содержит результаты сравнения электромагнитной помехи в межсоединении МПП СВТ при широкополосном электромагнитном воздействии, полученные с применением предложенных аналитических и имитационных моделей, и результатов экспериментальных исследований других авторов. Пример 4 включает результаты прогнозирования и сравнения электромагнитных помех в межсоединениях МПП СВТ при воздействии ЭМИ высотного ЯВ, полученные с применением предложенных аналитических и имитационных моделей и результатов экспериментальных исследований других авторов. Пример 5 включает сравнение результатов моделирования электромагнитных помех в неэкранированной витой паре при электромагнитных воздействиях, полученные с применением предложенных аналитических моделей, с экспериментальных данными, представленными в литературе. Пример 6 содержит результаты прогнозирования электромагнитных помех в неэкранированной витой паре при воздействии ЭМИ СЭТ.
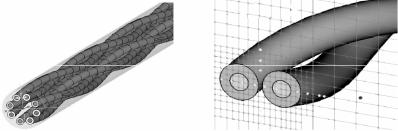
Пример 1. Анализ электромагнитной помехи в линии связи СВТ при воздействии ЭСР на его корпус. Конфигурация экспериментального стенда приведена на рис. 2.46 [201]. Материал корпуса – алюминий. Внутри корпуса, у верхней стенки расположен проводящий контур с размерами 40×40 мм. Один конец контура соединен с верхней стенкой, а другой конец нагружен на сопротивление 50 Ом. В передней части корпуса имеется щель (размеры
127
4×350 мм). Форма импульса тока ЭСР соответствует ГОСТ 51317.4.2-99 и максимальное значение составляет 4 А.
а |
б |
Рис. 2.46. Экспериментальный стенд (а) и его имитационная модель в графиче-
ском представлении (б): 1 – корпус; 2 – контур; 3 – нагрузка; 4 – щель; 5 – источник ЭСР
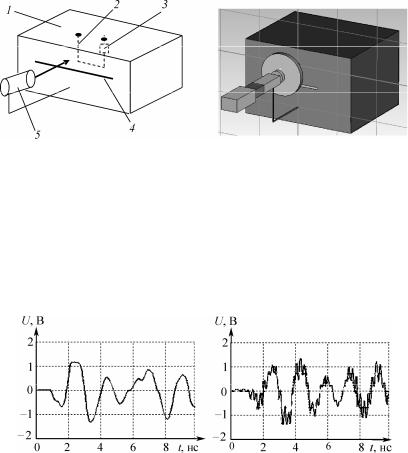
Прогнозируемая электромагнитная помеха в контуре внутри данного корпуса представлена на рис. 2.47, а. Максимальная величина помехи 1,15 В и форма имеет колебательный характер. Также, для сравнения, приведена электромагнитная помеха, полученная в экспериментальном стенде (рис. 2.47, б) [7].
а |
б |
Рис. 2.47. Электромагнитная помеха в линии связи СВТ:
а – моделирование; б – эксперимент
Пример 2. Анализ электромагнитной помехи в линии связи СВТ при воздействии ЭСР на специальную пластину связи. Кон-
128
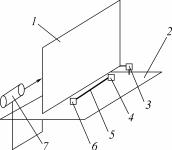
фигурация экспериментального стенда приведена на рис. 2.48 [7]. Материал горизонтальной и вертикальной пластины связи – алюминий. Вертикальная пластина связи соединена с горизонтальной пластиной посредством резистора 50 Ом. Воздействие источника ЭСР осуществляется в середину вертикальной пластины связи. Данная конфигурация экспериментальной установки определена в ГОСТ Р 51317.4.2-99 для проведения испытаний на воздействие ЭСР. Электромагнитная помеха наблюдается в контуре, образованном двумя проводниками радиусом 0,2 мм и расстоянием между ними 2,5 мм (провод мышки (клавиатуры) персонального компьютера). На ближнем конце контура нагрузка 50 Ом, на дальнем конце 105 Ом. Форма импульса тока ЭСР соответствует ГОСТ 51317.4.2-99 и максимальное значение составляет 4 А.
Электромагнитная помеха на нагрузке ближнего конца, полученная путем имитационного моделирования, представлена на рис. 2.49, а. Максимальная величина помехи 1,25 В. Форма помехи имеет колебательный характер. Для сравнения приведена электромагнитная помеха (рис. 2.49, б), полученная в экспериментальном стенде [7].
Рис. 2.48. Эскиз экспериментального стенда:
1 – вертикальная пластина; 2 – горизонтальная пластина; 3 – резистор; 4 – нагрузка на дальнем конце контура; 5 – контур; 6 – нагрузка на ближнем конце контура; 7 – источник ЭСР
129
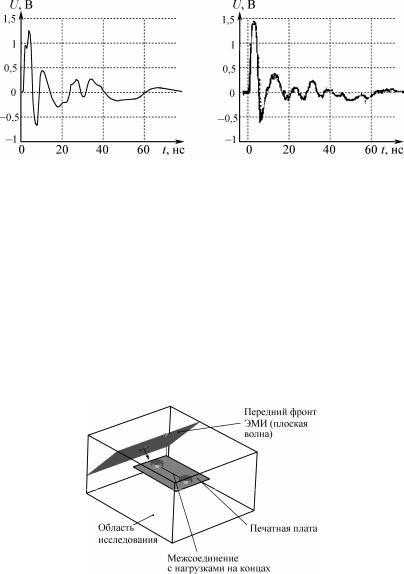
а |
б |
Рис. 2.49. Электромагнитная помеха в исследуемой линии связи СВТ:
а – моделирование; б – эксперимент
Пример 3. Для прогнозирования электромагнитных помех в межсоединениях МПП при широкополосном электромагнитном воздействии разработана имитационная модель (рис. 2.50) [250].
Исходные данные: структура МПП (рис. 2.37); размеры МПП – 200 ×150 мм; толщина основания – 1,5 мм; материал осно-
вания – εr = 4,7; длина межсоединения – 100 мм; ширина межсо-
единения – 1 мм; толщина межсоединения – 35 мкм; нагрузка на концах межсоединения – 50 Ом; углы падения и поляризации воздействующего ЭМИ – θ = 45, φ = γ = 0.
Рис. 2.50. Графическое представление имитационной модели для анализа электромагнитных помех в межсоединении МПП
130
