Гизатуллин монография 1

V0,L ~ e j ( mβ−kx ) L − 1 = 2sin[(mβ − kx )L / 2].

Поэтому максимальная величина передаточной функции

(2.14) определяется как:

(mβ − kx )L / 2 = (β ± kx )L / 2 = π n, 2

где n = 1,2,3...

Это приводит к следующему соотношению для соответст-

вующих резонансных частот:

где с0 – скорость света.

Первая резонансная частота, рассчитанная по (2.17) при n = 1

может быть расценена как верхний предел для дальнейшего низ-

кочастотного приближения. Это становится возможным из-за того,

что на практике, в большинстве случаев, межсоединения МПП ко-

ротки по сравнению с минимальной длиной волны в спектре рас-

сматриваемых широкополосных электромагнитных воздействий.

Это дает возможность еще упростить конечные выражения для передаточной функции:

111

Электромагнитные помехи в межсоединениях МПП в области до одного ГГц для произвольной плоскости падения плоской электромагнитной волны и полных сопротивлений на концах межсоединений вычисляются заменой (2.15) в (2.10). Снова, со ссылкой к (2.11), для случая Z0,L Zc , конечные передаточные функции становятся:

Мы видим, наводимая помеха прямо пропорциональна частоте воздействия ( k0 = ω / c0) и площади контура (межсоединение МПП и обратный проводник) ( hL). Последний указывает на прямую зависимость восприимчивости контуров на МПП от его геометрических параметров.

Максимальная величина выражения (2.19) относительно углов θ, φ, γ, получается при γ = 0° /180°, соответствующей макси-

мальному электромагнитному полю воздействующего на контур. Это приводит к следующему выражению:

Этот результат ясно отображает влияние диэлектрической постоянной подложки МПП. В пределах практического диапазона

112

ленно уменьшается только для более высоких значений εr . Напри-

мер для наиболее распространенного материала подложки FR-4 ( εr = 4,7) его значение находится в диапазоне 0,4. Например, при

εr = 10 это соотношение равняется 0,25, т.е. изменение только на

12 %. Следовательно, использование подложек с более высокой диэлектрической проницаемостью имеет только незначительное влияние на восприимчивость контуров МПП.

При условии, что нагрузки на концах контуров МПП имеют линейную характеристику или они могут быть линейно приближены в данном диапазоне частот, электромагнитные помехи во временной области при внешнем произвольном электромагнитном воздействии могут быть рассчитаны посредством Фурье преобразования, используя полученные решения в частотной области. Взаимо-

связь частотной V0,1 (ω) и временной областей V0,1 (t ) дается как:

+∞

V0,1(t ) = 2π1 −∞∫ V0,L (ω)e jωt dω.

Амплитуда напряженности электрического поля E i , входя-

щая в уравнение для нахождения V0,1 (ω) , может быть получена пу-

тем прямого преобразования Фурье из временной функции переходного процесса Ei (t ) :

+∞

E i (ω) = ∫ Ei (t)e− jωt dt .

−∞

Если для отношения сопротивлений выполняет условие Z0,L Zc , и уравнение (2.16) является адекватным, то можно полу-

чить простое решение во временной области:

113

Используя свойства временного сдвига Фурье преобразования

e− jωT Ei (ω) → Ei (t − T ),

мы получаем следующее решение во временной области:

Если спектральное распределение функции напряженности Ei (t) главным образом сконцентрировано в области относительно низких частот можно непосредственно получить более простое решение, основанное на приближении низкой частоты. Получаемое решение пропорциональна jω , которая переводится во вре-

менную область следующим образом:

jωEi (ω) → d Ei (t). dt

Таким образом, полное приблизительное решение во временной области получается пропорциональной производной времени Ei (t ) :

114

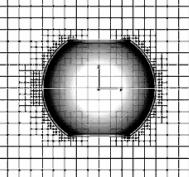
В целом, по итогам сравнения (раздел 2.8) мы видим, что результаты моделирования электромагнитных помех в межсоединениях МПП и экспериментальные результаты хорошо совпадают (расхождение не более 15 %) [250]. Но, аналитический подход, рассмотренный в данном разделе, имеет ряд существенных ограничений и допущений, что сильно ограничивает его применение на практике и служить для быстрой оценки электромагнитных помех в межсоединениях МПП СВТ при широкополосных электромагнитных воздействиях. В связи с этим, для анализа электромагнитных помех в межсоединениях МПП СВТ внутри зданий при внешних широкополосных электромагнитных воздействиях реализованы имитационные модели, основанные на полноценном решении уравнений Максвелла в трехмерной области, методом определенных интегралов [250, 259]. Для моделирования сложной конструкции МПП и корпуса СВТ внутри здания при внешних широкополосных электромагнитных воздействиях предлагается использовать метод подсеток. Он позволяет линиям разбиения начинаться и заканчиваться в любой точке анализируемого объема и благодаря этому получать вблизи элементов произвольной формы с малы-

115

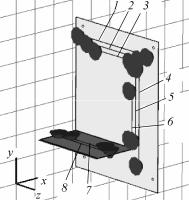
магнитных помех в межсоединениях МПП вне или внутри корпуса

СВТ при широкополосных электромагнитных воздействиях [259]. МПП имеет размеры 310×240×2,65 мм (расположение вертикальное)

и 170×200×2,65 мм (расположение горизонтальное), соответственно. Как правило, данные МПП располагаются внутри корпуса СВТ. Длина исследуемых межсоединений в МПП (8 шт.) – 100, 150, 200 мм (ориентация горизонтальная и вертикальная). Ширина контуров (толщина изоляционного слоя МПП) – 0,86 мм; материал изоляционного слоя FR-4 (диэлектрическая проницаемость ε = 4,9). Ширина межсоединений – 0,25 мм. Нагрузка на концах межсоединений – произвольная.

Рис. 2.41. Графическое представление имитационной модели для анализа электромагнитных помех в межсоединениях МПП СВТ при широкополосных электромагнитных воздействиях

Преимущества имитационных моделей для анализа электро-

магнитных помех в МПП СВТ: точное воспроизведение конструк-

ции МПП; произвольная ориентация воздействующего ЭМИ; учет резонансных эффектов; произвольная нагрузка; анализ до сверх-

высоких частот.

116

2.7. Математические модели для анализа электромагнитных помех в локальной сети

Неэкранированная витая пара является основой для построе-

ния локальной сети СВТ и систем зданий, а по своим электрофи-

зическим и геометрическим параметрам выступает хорошим «при-

емником» электромагнитных полей. Конструкция неэкранированной витой пары может быть представлена периодической структурой в виде бифилярной спирали скрученной относительно средней ли-

нии (рис. 2.42) [260 – 262]. В наиболее распространенном инфор-

мационном кабеле категории 5 и 5е содержится четыре таких пар внутри общей оболочки.

Рис. 2.42. Конструкция неэкранированной витой пары

Координаты точек a(l), b(l) внутри проводников витой пары определяется следующим образом (рис. 2.43):

где l – длина дуги; s – расстояние между осями проводников витой пары; p – шаг скрутки проводников витой пары; a – коэффициент скрутки, который определяется следующим образом:

117

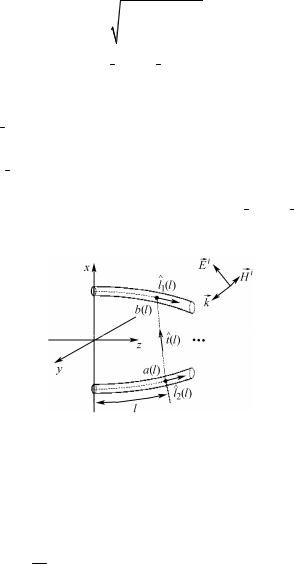
Единичные векторы l1(l) и l2 (l) направлены по касательной

к проводникам 1 и 2, соответственно, в точках a(l) и b(l) (рис. 2.43).

Рис. 2.43. Изменение координат проводников витой пары в плоскости x – y

при изменении координат в направлении оси z

Для данного случая, уравнения линии передачи при воздей-

ствии внешних неоднородных электромагнитных полей можно записать в следующем виде [262, 263]:

d V (l) = -ZI (l) +VF (l); Z = Zi + jωLe; dl

118

a( l )

t(l) = cos(a × l)ax + sin(a × l)a y .

где ρ – цилиндрическая координата в радиальном направлении; t(l) – единичный вектор направленный из точки a(l) в точку b(l); l – длина дуги по проводнику, переменная которая однозначно оп-

ределяет позицию всех точек наблюдения вдоль передачи-линии; uur

Ei ( x(l), y(l), z(l)) – вектор электрической напряженности внешне-

го электромагнитного поля; V (l) – напряжение между линиями передачи (положительное в точке b(l), отрицательное в точке а(l)); I (l) – ток в линиях передачи; Z – полное сопротивление линии передачи на единицу длины; Zi – активное сопротивление линии передачи на единицу длины; Le – индуктивность линии передачи на единицу длины; Y – полная проводимость линии передачи на единицу длины; G – проводимость изоляции вокруг линии передачи на единицу длины; C – емкость линии передачи на единицу длины; VF (l) и IF (l) – распределенные зависимые источники на-

пряжения и тока, соответственно.

Данные уравнения (2.20) можно рассматривать как модификацию известных уравнений однородных линий передачи, только,

119

в рамках данной работы, распределенные источники VF (l) и IF (l)

учитывают винтовой характер линий передачи витой пары. Рассмотрим ограничения данных уравнений:

1.Изоляция вокруг проводников линии передачи считается однородной диэлектрической средой. На практике проводники витой пары покрыты тонким слоем изоляции. При этом его толщина всегда намного меньше наименьшей длины волны воздействующего электромагнитного поля, поэтому можно считать ее однородным диэлектрическим слоем.

2.Индуктивность Le и емкость C линии передачи на едини-

цу длины считаются независимыми от положения по длине, так как, во-первых, расстояние между осями проводников линии передачи всегда остается неизменным в плоскости x – y, и, во-вторых, период скрутки линии передачи намного больше чем расстояние между осями проводников витой пары ( p >> s). Данное предположение дает возможность решения задачи для случая однородной линии передачи, а все первичные параметры линии передачи на единицу длины рассчитываются по известным формулам для двухпроводной цилиндрической линии передачи [158]:

где μ0 , e0 – магнитная и диэлектрическая проницаемость вакуума, соответственно, m0 = 4 × p×10−7 [Гн/м], e0 = 8,854 ×10−12 [Ф/м]; μr , er – магнитная и диэлектрическая проницаемость изоляции про-

водников витой пары.

3. Минимальная длина волны воздействующего электромагнитного поля намного больше расстояния между осями проводников неэкранированной витой пары ( λ >> s ).

120