
Гизатуллин монография 1
.pdfрезонансными частотами между 100 МГц и 2 ГГц данные ЭМИ оказывают наибольшее влияние по энергии, несмотря на то, что его общая энергия значительно меньше чем энергия других импульсов. ЭМИ ЭСР и ЭМИ высотного ЯВ (вариант 1) обладают наибольшей эффективностью воздействия на линии связи СВТ длиной от 1 до 10 м. ЭМИ высотного ЯВ (вариант 2) и «быстрый» ЭМИ разряда молнии наиболее эффективно воздействуют на линии связи СВТ длиной от 10 до 100 м. Эффективность воздействия «медленного» ЭМИ разряда молнии наиболее сильно проявляется для линий связи длиной более нескольких сот метров. Таким образом, опасность воздействия конкретного ЭМИ определяется не только амплитудой, фронтом импульса и энергией, но и эффективностью его воздействия по энергии и напряжению.
Таблица 2.22
Эффективность широкополосных электромагнитных воздействий на линии связи различной длины
|
Полоса |
|
|
Эффективность воздействия импульса ηЕ |
|
||||
|
|
(номера импульсов соответствуют табл. 3.3.3) |
|||||||
L, м |
частот, |
|
|||||||
|
|
|
|
|
|
|
|||
|
МГц |
1 |
|
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
|
|
|
0,1 |
840 |
– 2040 |
0,277 |
|
8,1·10 –3 |
3,9·10–3 |
2,8·10–4 |
8,4·10–8 |
1,7·10–11 |
1 |
84 |
– 204 |
0,112 |
|
0,107 |
0,162 |
0,017 |
8,3·10 –5 |
1,7·10–8 |
10 |
8,4 |
– 20,4 |
0,011 |
|
0,232 |
0,18 |
0,161 |
0,052 |
1,7·10 –5 |
100 |
0,8 – 2 |
1,2·10 –3 |
|
0,031 |
0,02 |
0,171 |
0,313 |
0,017 |
|
Следующее условие возникновения резонансных явлений определяется особенностями конструкции современных СВТ. Замкнутый металлический корпус СВТ является электромагнитным экраном защищающий функциональные узлы внутри корпуса от воздействия нежелательных электромагнитных полей. Процесс движения электромагнитной энергии в замкнутом корпусе сопровождается рядом явлений, к которым относятся и резонансные явления. Данное явление может привести к нарушению условий функционирования электромагнитного экрана, т.е. к недопустимо-
101
му снижению его эффективности. При резонансе амплитуда напряженности поля внутри замкнутого экрана возрастает в Q раз, а следовательно, эффективность экранирования уменьшается в Q раз относительно результирующей эффективности, учитывающей поглощение и отражение электромагнитных волн [142]. Для приближенной оценки резонансных частот корпусов СВТ применяется выражение:
|
m 2 |
n 2 |
||||
fрез =150 |
|
|
|
+ |
|
|
l |
|
|||||
|
|
|
b |
|||
+p 2
, МГц,h
где l, b, h – геометрические размеры сторон корпуса, м; m, n, p – индексы, обозначающие число стоящих полуволн, укладывающихся вдоль сторон корпуса. На резонансных частотах напряженность электрического поля внутри корпуса для СВТ определятся выражением [142]:
E1 |
»110 × |
|
|
P × Ко |
|
, |
|
|
- Ко )∑ S |
||||
|
(1 |
|
|
|||
где Р – мощность источника электромагнитного поля; Ко – коэффициент отражения внутренней поверхности стенок корпуса (0 < Ко < 1); ∑ S – суммарная площадь внутренней поверхности стенок корпуса.
Следовательно, напряженность электрического поля внутри корпуса СВТ при собственных резонансных частотах определяется коэффициентом отражения от внутренней поверхности стенок и ана-
литически обусловлено множителем 4 × Kо . 1 - Ко
Резонансные частоты реальных металлических корпусов СВТ, на практике, во многих случаях не соответствуют расчетным, так как из-за наличия внутри корпуса функциональных узлов происходит существенное изменение электромагнитной обстановки внутри корпуса и сдвиг данных частот, преимущественно, в сторо-
102
ну повышения. Например, рассмотренные примеры (рис. 2.30, 2.31) показывают, что появляются всплески напряженности на частотах, которые не соответствуют расчетным. В последующих примерах (рис. 2.32) прогнозирование электромагнитных помех в линиях связи находящихся внутри корпусов современных цифровых СВТ отчетливо показывает всю сложность электромагнитной обстановки и актуальность учета резонансных эффектов для ЭСР, ЭМИ СЭТ. Таким образом, полноценный учет резонансных частот внутри корпусов современных цифровых СВТ является важной задачей и его решение требует применения других, более эффективных инструментов и численных методов.
Следующим фактором возможного возникновения резонансных эффектов в линиях связи СВТ при широкополосных электромагнитных воздействиях, является то, что данные СВТ находятся внутри здания. Таким образом помещения зданий, где располагаются современные цифровые СВТ, по аналогии с корпусами СВТ являются объемными резонаторами. Например, можно примерно
рассчитать собственные резонансные частоты помещений: размеры 5×3,5×4 м – резонансные частоты 48 МГц, 52 МГц, 57 МГц, 64 МГц; размеры 7×5×4 м – частоты 37 МГц, 43 МГц, 48, 53 МГц; размеры 9×7×4 м – частоты 27 МГц, 41 МГц, 43 МГц, 46
МГц. Таким образом, резонансные эффекты внутри здания в основном, актуальны для внешних широкополосных ЭМИ высотного ЯВ и СЭТ. Также, в результате проведенного анализа эффективности экранирования стен зданий, выявлено, что можно наблюдать
резонансные явления, связанные с железобетонной арматурой стен (ячейки 20×20 см, 20×40 см, 20×60 см) при воздействии ЭМИ СЭТ.
Таким образом, резонансные эффекты при широкополосных электромагнитных воздействиях в линиях связи СВТ внутри здания могут быть связаны с несколькими причинами: длиной линий связи (антенный эффект); металлическим замкнутым корпусом СВТ; помещением зданий, где расположены СВТ; с особенностя-
103
ми конструкции стен зданий. Так как при данных явлениях проявляется наибольшей отрицательный эффект для помехоустойчивости СВТ при внешних широкополосных электромагнитных воздействиях, а упрощенные аналитические подходы не дают возможности полноценно учесть данные эффекты, необходимо применять эффективный инструмент на базе численных методов и средств трехмерного электромагнитного моделирования, и адекватные математические модели.
2.6. Математические модели для анализа электромагнитных помех в межсоединениях печатных плат
Для прогнозирования помехоустойчивости СВТ построенного на основе печатной платы необходимо провести анализ электромагнитных помех на межсоединениях данной печатной платы, к которым подключаются цифровые элементы. В первом приближении можно рассматривать случай, когда печатная плата находится в открытой области. Известны некоторые аналитические работы [252 – 254, 257], в которых рассматриваются в частотной и временной областях данные задачи для неоднородных полосковых линии передачи. Но исследования, основанные на модели линии передачи с распределенными источниками, прежде всего, относятся к интегральным схемам, имеющих другие геометрические параметры и работающие в более высоких частотах, чем печатная плата. Авторы разрабатывают общие, но очень сложные формулы для разности потенциалов и распределения тока по контуру.
Рассматриваемое решение направлено на прикладной диапазон параметров печатной платы и поэтому представляет практический интерес. Первичная цель данного раздела работы состоит в том, чтобы обеспечить конечными аналитическими формулами, с помощью которых легко можно рассчитать электромагнитные помехи при широкополосных электромагнитных воздействиях во
104

временной области [250]. В работе печатная плата рассматривается как слоистая структура с микрополосковой линией передачи с ква- зи-TEM моделью распространения. Сечение структуры микрополосковой линии передачи представлена на рис. 2.37.
Рис. 2.37. Сечение печатной платы с микрополосковой линией передачи
Конструктивно она соответствует МПП с потенциальными слоями, применяемыми в современных СВТ. Квази-TEM модель работает для достаточно низких частот, когда незначительны продольные составляющие поля. В пределах этого квазистатического диапазона частот линия передачи может быть описана первичными параметрами на единицу длины. Обычно к вторичным параметрам относятся эффективная относительная диэлектрическая постоянная ereff и характеристический импеданс Zc . Коэффициент танген-
са угла потерь системы диэлектрических слоев, также как удельные сопротивления проводника являются относительно маленькими, так чтобы потерями можно пренебречь для обычной продолжительности линии передачи. С увеличением частоты параметры линии передачи становятся все более частотно зависимыми и квазиTEM предположение постепенно перестает работать. Область перехода очень плавная и его можно описать следующим выражени-
ем [255]:
fgstat |
= |
21,3 ×106 |
|
(2.9) |
|||
|
|
|
|
||||
(w + 2 |
× h) er |
+1 |
|||||
|
|
|
|||||
Для типичных размеров МПП данная частота может расположиться от 1 до 10 ГГц, поэтому для решения ранее поставленных задач анализа электромагнитных помех при рассматриваемых широкополосных электромагнитных источниках квази-TEM предположение будет работать. Различные выражения для ereff и Zc ,
105

в законченных формах, были развиты в работе [256]. Они зависят от относительной диэлектрической постоянной подложки er , от-
ношения ширины линии передачи и толщины подложки w / h, отношения толщины линии передачи к толщине подложки t / h . Достаточно точные выражения приведены ниже:
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
e +1 |
|
e -1 |
|
10 |
|
|
|
|
||||
e = |
r |
|
+ |
r |
|
1 + |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
||||||
reff |
2 |
|
|
2 |
|
|
w |
|
|
|
|||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
h |
|
|
|
|||
|
|
60 |
|
|
× h |
|
w |
|
|
|
||||
|
|
ln |
8 |
+ |
eff |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
e |
|
w |
4 × h |
|
|
||||||
|
|
reff |
|
|
eff |
|
|
|
|
|||||
Zc |
= |
120p weff |
|
|
|
weff |
|
|||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
+1,393 + 0,667 × ln |
|
+1,444 |
||||
|
|
|
|
|
|
|
||||||||
|
|
ereff |
|
|
||||||||||
|
|
|
|
h |
|
|
|
h |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1
w £ 1, h
w ³ 1; h
weff
h
=w + h
|
|
|
|
|
|
|
|
w |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
+ ln |
|
4 × p |
|
h |
|||||
|
1 |
|
t |
||||||||||
t |
|
|
|
||||||||||
1,25× |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|||||||||
h |
|
|
|
|
h |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 + ln |
|
|
|
|
|
||||
|
|
|
t |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
h |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
w |
£ |
1 |
, |
|||
|
|
2 × p |
||||
h |
|
|
|
|||
w |
³ |
|
1 |
. |
||
|
|
|||||
h |
|
2 × p |
|
|
||
Токи и разности потенциалов, наводимые на межсоединения МПП внешними электромагнитными полями, описываются теле-
графными уравнениями. Если определены нагрузки, выражения принимают компактную матричную форму, известную как BLT
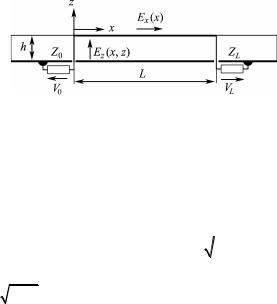
уравнения [258]. В явной форме BLT уравнения для напряжений на нагрузки в частотной области представляются в виде (рис. 2.38):
106
V |
|
|
1 |
|
(1 + r0 ) ×(rL S1 |
+ e jβL S2 ) |
|
||
0 |
|
= |
|
(1 + rL ) × (e jβL S1 |
. |
(2.10) |
|||
e j 2βL - r0rL |
|||||||||
VL |
|
|
+ r0 S2 ) |
|
|||||
|
|
|
|
|
|
|
|
|
|
Рис. 2.38. Продольное сечение печатной платы
Коэффициенты отражения r0,L и постоянная распростране-
ния волны b вычисляются через полные сопротивления нагрузки
Z0 и ZL :
r0,L |
= |
Z0,L |
- Zc |
; β = k0 |
|
, |
|
εreff |
|||||||
Z0,L |
|
||||||
|
|
+ Zc |
|||||
где k0 = w 
 m0e0 вычисляется как произведение волнового числа свободного пространства и угловой частоты.
m0e0 вычисляется как произведение волнового числа свободного пространства и угловой частоты.
Для случая, когда сопротивления нагрузки Z0, ZL и волно-
вое сопротивление линии передачи Zс равны, коэффициенты от-
ражение r0,L равны нулю. Тогда выражения (2.10) преобразуются
к упрощенному виду, которые также хорошо аппроксимируют дан-
ные процессы:
V |
@ e− jβL S , |
(2.11) |
0,L |
2,1 |
|
когда Z0,L @ Zc.
107
Внешние воздействующие электромагнитные поля могут быть представлены распределенным источниками тока и напряже-
ния в зависимости от используемой формулировки. В данной слу-
чае выбрана так называемая формулировка разности распределен-
ных потенциалов, в которой учитываются только касательные электрические составляющие поля. Интегрирование этих распре-
деленных источников напряжения по строке описано коэффициен-
тами S1,2 следующим образом:
S1 |
|
= |
1 |
|
υ0 + υ+x − υLe jβL |
|
|||||
|
|
|
|
|
|
jβL |
− |
jβL |
|
, |
|
|
|
|
|
||||||||
|
2 |
|
−υ0e |
|
|
||||||
S2 |
|
|
|
|
− υx e |
|
+ υL |
||||
где υ0,L = ∫ Ez ( x1,2 , z )dz ; |
|
|
|
|
|
|
L |
|
|
||
x1,2 |
= 0, L и υ±x = ∫ Ex ( x)e± jβx dx . |
||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
Воздействующие электрические поля Ex (x)
(2.12)
и Ez (x, z)
(рис. 2.38) рассматриваются как составляющие плоской электромагнитной волны произвольной ориентации. При этом произвольная, линейно поляризованная плоская волна, подающая со стороны верхнего полупространства, определена углами падения θ и φ,
иуглом γ поляризации. Необходимо разделить произвольную плоскую электромагнитную волну на горизонтальную TE и вертикальную TM составляющую (рис. 2.39). Тогда, горизонтальная TE
ивертикальная составляющая TM могут рассчитываться по отдельности:
E TE = E sin γ ; |
E TM = E cos γ . |
||
i |
i |
i |
i |
Поперечный разрез печатной платы представляет собой планарную трехслойную среду, состоящую из воздушной области (ε0 ,μ0 ), диэлектрической подложки (ε0εr ,μ0 ) и идеального прово-
дящего слоя (k → ∞) . В данной работе принята общая теория пло-
ских структур с кусочно-однородными электрическими свойствами.
108
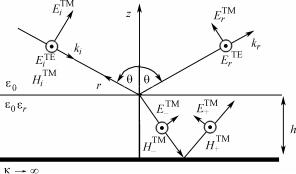
Рис. 2.39. Распределение составляющих электромагнитного поля в трехслойной среде печатной платы
Точная передаточная функция между межсоединением печатной платы и воздействующим ЭМИ может быть рассчитана для произвольных полных сопротивлений на концах и волновых сопротивлений по следующим выражениям:
×
V0,L
fx (θ,φ,
mEi |
e jβ( x2 ,1−L) e j ( mβ−kx ) L − 1 |
× |
|
|
||||||
2 |
|
j(mβ − kx ) |
|
|
|
|||||
|
|
|
|
|
||||||
|
|
|
|
1 − e− jk2 z 2h |
|
|||||
γ) − j(mβ − kx ) fz |
(θ,φ) |
|
|
. |
(2.13) |
|||||
jk2 z |
||||||||||
|
|
|
|
|
|
|
||||
Для печатаных плат коэффициенты S1,2 (2.12) могут быть
значительно упрощены, учитывая тот факт, что высота подложки МПП обычно намного меньше, чем длина волны распространяющейся в подложке. Использование данного предположения приводит к следующему упрощению:
e− jk2 z 2h ≈ 1− jk2 z 2h для k2 z 2h << 1,
что далее приводит к следующим выражениям:
1− e− jk2 z 2h |
cos γ sin θ |
||
|
≈ 2h ; fz (θ,φ) ≈ |
|
. |
|
|
||
jk2 z |
εr |
||
109

Также функция fx (θ,φ, γ) может быть значительно упроще-
на, разлагая в ряд Тейлора для параметра k2 z 2h до линейного чле-
на, который приведет:
fx (θ,φ, γ) ≈ |
|
|
|
ε |
|
− sin2 θ |
+ sin φsin γ cos θ |
|
|||
j2hk0 cos φcos γ |
|
r |
|
εr |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Использование ранее указанных упрощений вместе с отно- |
|||||||||||
шением: |
|
|
|
|
|
|
|
|
|
|
|
|
±β − kx |
= k0 (± |
|
|
− sin θcos φ), |
|
|||||
|
εreff |
|
(2.14) |
||||||||
дает следующий, намного более простой результат для S1,2 : |
|
||||||||||
|
S ≈ ± jk hE e jβx1,2 |
e j ( ±β−kx ) L − 1 |
× |
|
|||||||
|
|
j(±β − kx ) |
|
|
|||||||
|
1,2 |
0 i |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
εreff |
|
× sin φsin γ cos θ + cos φcos γ m |
|
|
|
εr |
|
|
||
|
|
|
sin θcos γ . (2.15)
Передаточную функцию можно рассчитать, заменяя (2.15)
в (2.10). Для случая Z0,L Zc передаточная функция (2.11) имеет следующий вид:
V |
≈ m jk hE e jβ( x2,1−L) |
e j ( mβ−kx ) L − 1 |
× |
|
|||||
j(mβ − kx ) |
|
|
|||||||
0,L |
0 |
i |
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εreff |
|
|
|
||
× sin φsin γ cos θ + cos φcos γ ± |
|
sin θcos γ . |
(2.16) |
||||||
|
εr |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если знаменатель заменить выражением (2.14), из этого сле-
дует, что величина напряжений на зажимах V0,L изменяется с час-
тотой в следующей зависимости:
110
