
Расчет стержней и стержневых систем
.pdf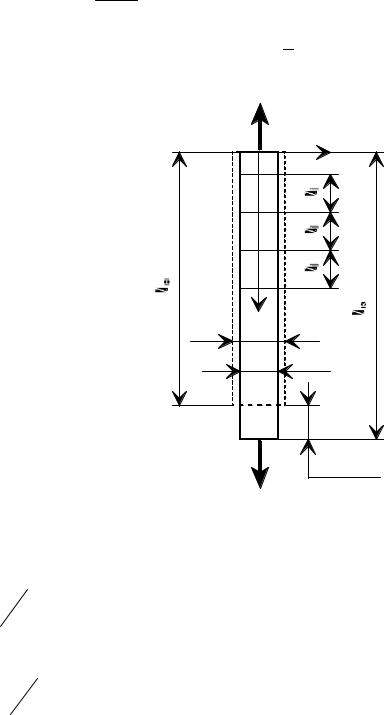
|
|
|
|
|
|
|
|
61 |
|
|
|
|
|
|
стержня, надо ввести в рассмотрение относительную величину |
|
|||||||||||||
|
|
|
|
|
ε = |
|
l |
= |
lђ |
− l’ |
, |
(2.2) |
||
|
|
|
|
|
l |
|
l |
|
||||||
|
|
|
|
|
|
|
|
|
’ |
|
|
|||
|
|
|
|
|
|
|
|
’ |
|
|
|
|
|
|
которая называется относительным удлинением или линейной деформацией. |
||||||||||||||
Она представляет собой отношение приращения длины к первоначальной дли- |
||||||||||||||
не и является безразмерной величиной. За- |
|
R=P |
|
|||||||||||
метим, что при малых деформациях в зна- |
|
y |
||||||||||||
менателе формулы (2.2) можно использо- |
|
A=A* |
||||||||||||
вать как lн, так и lк − разница в результатах |
|
|
||||||||||||
будет пренебрежимо малой. |
l = εlн , |
|
|
|
|
|
|
|
||||||
Из (2.2) следует, что |
|
или в |
|
|
|
|||||||||
других обозначениях: u(xB ) = εxB . |
|
|
|
|
|
|
|
|
||||||
Поскольку |
любую |
часть |
стержня |
|
|
|
||||||||
можно рассматривать как стержень мень- |
|
|
|
|||||||||||
шей длины, нагруженный той же силой |
|
x |
|
|||||||||||
N (x) = P , то для любой точки стержня пе- |
|
bн |
|
|||||||||||
ремещение есть |
. |
|
|
|
|
|
|
|
|
|
|
|
bк |
|
|
% |
|
|
|
|
|
|
|
|
|
|
|
|
|
u ( x ) = ε x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Однако не очевидно, что |
% |
|
Покажем |
|
|
|
||||||||
ε = ε. |
|
B |
|
|||||||||||
это. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B* |
|
|
На стержне выделим участки равной |
|
l = uB |
||||||||||||
длины (2.3). Обозначим длину участка l1. |
|
P |
||||||||||||
|
|
|||||||||||||
Абсолютное удлинение участка обозначим, |
|
Рис. 2.3 |
|
|||||||||||
естественно, |
l1. Это удлинение одинаково |
|
|
|
||||||||||
для всех ячеек сетки, так как они одинаковы и растянуты одинаковыми силами. |
||||||||||||||
Тогда и относительное удлинение у всех участков одинаково: |
|
|||||||||||||
|
|
|
ε1= |
|
l1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 1 |
|
|
|
|
|
|
|
|
|
Если взять теперь участок стержня длиной, например, 3l1, то его абсолют- |
||||||||||||||
ное удлинение будет равно 3 |
l1, а относительное |
|
||||||||||||
|
|
|
ε 3= |
3 |
l1 |
|
= ε |
1= ε = const . |
|
|||||
|
|
|
|
|
3l1 |
|
|
|
|
|
|
|
|
|
Поскольку аналогичным образом можно показать постоянство деформации для |
||||||||||||||
любого участка длины стержня, приходим к выводу о том, что величина ε в |
||||||||||||||
данной задаче есть величина постоянная, и тогда перемещения точек связаны с |
||||||||||||||
относительным удлинением соотношением |
|
|
|
|
||||||||||
|
|
|
u(x) = εx , |
|
|
|
|
|
|
|
|
(2.3) |
||
где ε = const . Существования данной зависимости следовало ожидать, так как |
||||||||||||||

62
обе величины u и ε характеризуют одно и то же деформированное состояние. Эпюры линейных деформаций ε и осевых перемещений u (x) изображены на
рис. 2.1.
Помимо деформации удлинения в продольном направлении происходят также деформации сжатия в поперечном направлении. Если bк − толщина стержня после деформации, bн − толщина до деформации, то абсолютное су-
жение есть
b = bк − bн < 0 .
Относительное сужение или линейная деформация в поперечном направ-
лении по аналогии с предыдущим безразмерная величина:
εп = b |
< 0 . |
(2.4) |
|
bн |
|
Экспериментом установлено, что деформации в продольном и поперечном направлениях связаны соотношением
εп = −με , |
(2.5) |
где μ − безразмерная константа, определяемая экспериментально. Для разных материалов она имеет разные значения в зависимости от их физических свойств и называется коэффициентом Пуассона. Можно показать, что этот коэффициент принимает значения от 0 до 0,5 (обычно его значения лежат в пределах 0,15 ÷ 0,4 ; для сталей и дюраля он около 0,3).
2.1.2. Уравнения равновесия и напряженное состояние невесомого стержня
Пользуясь уравнением равновесия в направлении продольной оси стержня, мы получили значение внутренней растягивающей силы в стержне. Она постоянна и равна внешней нагрузке: N(x)=P.
Рассмотрения сил N, однако, недостаточно для решения вопроса о прочности. Ведь при одной и той же силе N, допустим в 1000 Н, материал колонны здания будет недогружен, а оси механизма наручных часов − перегружен. Ясно, что о нагруженности материала, а следовательно, и о прочности следует судить по относительной величине, т.е. по величине силы, приходящейся на единицу площади поперечного сечения стержня F:
σср = N F = σ . (2.6)
Величина σ называется нормальным напряжением (нормальным – поскольку используется сила, действующая по нормали к сечению). По итогам эксперимента принята гипотеза плоских сечений, свидетельствующая о том, что осевая сила распределяется равномерно по поперечному сечению. Поэтому вычисляемое по формуле (2.6) среднее напряжение σср равно напряжению в каждой точ-
ке σ. Измеряется напряжение в силах на единицу площади, т.е. в ньютонах на

63
квадратный метр (паскалях) (Н м2 = Па) в системе СИ, как и давление. Да это и
есть давление соседних слоев материала друг на друга, но в данной задаче это давление на отрыв. Если рассмотреть задачу сжатия, то нормальное напряжение окажется обычным давлением соседних поперечных сечений друг на друга.
Но Н м2 очень малая единица измерения и в практических расчетах обычно ис-
мм2 = МПа , а также
Эпюра нормальных напряжений в поперечных сечениях в данной задаче постоянна по длине стержня (рис. 2.1), постоянны напряжения и в пределах поперечного сечения; иными словами, нормальное напряжение в поперечных сечениях постоянно в данной задаче.
2.1.3. Физические соотношения. Закон Гука
Нами рассмотрены деформации стержня и внутренние усилия (напряжения) в его материале. Но напряжения вызывают деформации стержня, и наоборот, деформации стержня вызовут напряжения, поэтому между величинами этих групп должны существовать определенные соотношения, зависящие от физических свойств материалов. Эти зависимости называются физическими соотношениями. Для большинства материалов до определенного уровня нагрузки напряжения и деформации связаны прямо пропорциональной зависимостью, которую записывают так:
σ = Eε . |
(2.7) |
Эта зависимость легко устанавливается в эксперименте на растяжение или сжатие стержня. Она представляет собой частный случай физических соотношений и называется законом Гука. Коэффициент пропорциональности E в
этой формуле называется модулем упругости первого рода, или модулем упру-
гости на растяжение-сжатие. Заметим, что модуль упругости измеряется в тех же единицах, что и напряжение.
Если в пределах действия закона Гука приложенную ранее нагрузку сбросить, то тело полностью восстановит свою первоначальную форму.
Свойство твердых тел полностью восстанавливать свою первоначальную форму после снятия нагрузки называется упругостью.
Вспоминая формулы для напряжений и деформаций, получаем соотноше-
ния для других величин: |
|
|
|||||||
|
N |
= E |
|
|
l |
= E |
u(x) |
, |
|
|
F |
|
l |
|
x |
|
|||
|
|
|
|
|
|
|
|||
откуда |
|
|
|
|
|
|
|
|
|
|
N = EF |
|
l = EF u(x) . |
(2.8) |
|||||
|
|
l |
|
|
x |
|
|
||

64
Встречаются материалы упругие, но с нелинейной зависимостью между σ и ε. Для них физические соотношения отличаются от закона Гука. Другие физические соотношения действуют и при больших нагрузках, когда нарушается закон Гука.
Замечания.
1. Напряжения и деформации связаны друг с другом, сопровождают друг
друга. Поэтому состояние тела под нагрузкой называ- |
|
N(x)=P |
|
ют напряженно-деформированным состоянием, со- |
|
||
Nα |
|
||
кращенно НДС. |
|
||
|
α |
Tα |
|
2. Поперечная деформация происходит без на- |
|
|
|
пряжений в поперечном направлении. |
|
|
α |
|
|
|
|
3.В пределах действия закона Гука при сжатии большинство материалов имеет те же свойства, что и при растяжении.
4.НДС материала стержня при растяжении рас-
смотрено выше не в полном объеме. В сечениях, нор- |
B |
|
маль которых |
составляет некоторый угол α с про- |
P |
дольной осью |
стержня (рис. 2.4), легко обнаружить |
|
касательные напряжения, представляющие собой силу |
Рис. 2.4 |
|
в плоскости сечения Tα , приходящуюся на единицу его площади:
T = N (x)sinα , F = |
F |
, τ |
= Tα . |
|
|
||||
α |
α |
cosα |
α |
Fα |
|
||||
 Рассматривая деформацию элементов, мысленно вырезанных из растянутого стержня под углом к продольной его оси, найдем, что при деформациях ε > 0 и εп = −με < 0 углы элементов
Рассматривая деформацию элементов, мысленно вырезанных из растянутого стержня под углом к продольной его оси, найдем, что при деформациях ε > 0 и εп = −με < 0 углы элементов
прямыми не остаются. Особенно просто это видеть для элементов с проекцией в виде квадрата на плоскость чертежа, стороны которого составляют угол в 45° с продольной осью стержня (рис. 2.5). Угловая деформация, связанная с касательными напряжениями, таким образом, здесь также не рассмотрена.
Проверка прочности при расчете стержней на растяжение- Рис. 2.5 сжатие заключается в проверке выполнения условия прочности
по нормальным напряжениям
σ ≤ 
 σ
σ ,
,
где  σ
σ − допускаемое напряжение, представляющее собой некоторое опасное для данного материала значение, деленное на коэффициент запаса, соответствующий особенностям задачи.
− допускаемое напряжение, представляющее собой некоторое опасное для данного материала значение, деленное на коэффициент запаса, соответствующий особенностям задачи.
Это условие должно выполняться в каждой точке стержня. Поскольку до-

65
пускаемое напряжение обычно одинаково для всего стержня, его обычно запи-
сывают так:
σ max ≤  σ
σ
т.е. максимальное по модулю значение нормального напряжения не должно превышать допускаемое.
2.1.4. Пример решения задачи на растяжение и сжатие
Требуется проверить прочность и определить перемещение свободного конца стержня, изображенного на рис. 2.6. Здесь F, 1,3F, 1,4F − площади поперечных сечений, где F = 350 мм2; P, 1,2P, 1,5P − осевые силы; P = 30 кН; 1,8a, a, 1,5a − длины участков стержня, где a = 0,35 м. Места приложения сил выделены на рисунке жирной точкой. Материал: сталь Ст3; допускаемое напряжение которой [σ] = 160 МПа; модуль упругости E = 200000 МПа.
Решение задачи начнем с построения эпюры осевых сил в сечениях стержня, для чего следует воспользоваться общим алгоритмом построения эпюр. Поскольку стержень консольный, опорную реакцию определять не будем. Точки приложения сил разбивают стержень при построении эпюры на три отдельных участка (рис. 2.6). Далее согласно алгоритму к каждому участку в отдельности следует применить метод сечений для определения внутренних осевых сил N(x). Эпюра полученных осевых сил дана на рис. 2.6.
1,3F |
|
|
F |
|
|
1,4F |
|
|
|
P |
|
|
|
1,2P |
|
1,5P |
|
1,8а |
а |
|
1,5a |
|||||
21 Эпюра Ν (x), кН
-9 











-45
Эпюра σ (x), МПа
46,2
−25,7
−91,8
Рис. 2.6
Поскольку распределенных осевых сил нет, осевые силы оказываются постоянными в пределах участка, а эпюра представляет собой кусочно-

|
|
|
|
|
|
|
|
66 |
|
|
|
постоянную функцию. |
|
|
|
|
|
|
Участок CD. 0 ≤ x ≤1,5a . |
||||
|
|
N (x) |
|
|
1,5P |
|
|||||
|
|
|
|
|
åX i = 0 =1,5P + N (x ) , откуда |
||||||
|
|
|
|
|
|
|
|
|
|||
N (x) |
|
X |
|
|
x |
|
|
|
D N (x) = −1,5P = −45 кН . |
||
|
|
|
|||||||||
|
1,2P |
|
|
1,5P |
|
Участок BC. 1,5a ≤ x ≤ 2,5a . |
|||||
|
|
|
|
|
|
|
|
|
åX i = 0 = +1,5P −1,2P + N (x) , |
||
|
|
|
|
|
|
|
|
|
|||
X |
|
C |
x |
D |
|
N (x) = −0,3P = −9 кН . |
|||||
|
|
||||||||||
|
|
|
|
|
|||||||
N (x) |
|
|
|
P |
1,2P |
|
1,5P |
|
Участок AB. 2,5a ≤ x ≤ 4,3a. |
||
|
|
|
|
|
|
åX i = 0 = |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
B |
|
C |
x |
|
D |
|
=1,5P -1,2P - P + N (x), |
||
|
|
|
|
||||||||
|
|
|
|
N (x) = 0,7P = 21 кН . |
|||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
По осевой силе вычислим нормальные напряжения в сечениях стержня, а затем, воспользовавшись законом Гука и определением линейной деформации, найдем удлинения отдельных участков стержня:
|
|
|
|
|
|
|
|
|
Участок CD: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
σ(x) = |
|
N (x) |
= |
|
|
|
-45×103 Н |
|
|
|
= -91,8 |
Н |
|
|
, |
||||||||||||||||||||||
|
1,4F |
1,4 ×350 мм2 |
|
мм2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
σ |
|
|
-91,8 |
|
Н |
|
×1,5×0,35м |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
мм |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Dl = |
|
|
l |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= -0,241мм, |
|||||||||||||||
E |
|
|
|
200000 |
Н |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
мм |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
Участок BC: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
σ(x) = |
N (x) = |
|
-9×103 Н |
|
= -25,7 |
|
Н |
, |
|
||||||||||||||||||||||||||||
|
350 мм2 |
мм2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
σ |
|
|
|
|
-25,7 |
Н |
|
×0,35м |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
мм |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Dl = |
|
l = |
|
|
|
|
|
|
|
|
|
|
|
= -0,0450 мм, |
|||||||||||||||||||||||
E |
|
200000 |
Н |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
мм |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
Участок AB: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
σ(x) = |
N (x) = |
|
|
|
|
21×103 Н |
|
|
|
= 46,2 |
|
|
Н |
|
, |
|
|||||||||||||||||||||
1,3×350 мм2 |
|
мм2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1,3F |
|
|
|
|
|
|
|
||||||||||||||||||||||||

|
|
|
67 |
|
|
|
|
|||
|
σ |
46,2 |
Н |
|
×1,8×0,35м |
|
||||
|
мм |
2 |
|
|||||||
Dl = |
|
l = |
|
|
|
|
= 0,146 мм . |
|||
E |
200000 |
Н |
|
|
||||||
|
|
мм |
2 |
|
|
|||||
Эпюра распределения нормальных напряжений по длине стержня приведена на рис. 2.6. Алгебраически суммируя удлинения отдельных участков стержня, получим удлинение всего стержня:
l = lCD + lBC + lAB = −0,241 − 0,045 + 0,146 = −0,140 мм ,
т.е. стержень укорачивается.
В рассматриваемой задаче условие прочности выполняется, поскольку
91,8МПа <  160МПа
160МПа  .
.
2.1.5. Задание на выполнение расчетно-графической работы «Расчет стержней на растяжение и сжатие»
Построить эпюры осевых сил N(x) и нормальных напряжений s(x), проверить прочность и определить перемещения свободного конца стержня. Схему стержня взять с рис. 2.7 по номеру варианта, который сообщит преподаватель. На рис. 2.7 F - площадь поперечного сечения; P - осевая сила. Материал: сталь Ст3, [σ] = 160 МПа, E = 200000 МПа. Прочие данные взять из таблицы с помощью шифра.
Цифра шифра |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
F, мм2 |
в |
500 |
450 |
400 |
350 |
300 |
500 |
450 |
400 |
350 |
300 |
a, м |
б |
0,15 |
0,20 |
0,25 |
0,35 |
0,40 |
0,15 |
0,20 |
0,25 |
0,35 |
0,40 |
P, кН |
г |
35 |
30 |
25 |
20 |
15 |
35 |
30 |
25 |
20 |
15 |

68
1 |
1,6F |
F |
1,5F |
|
9 |
1,3F |
F |
1,5F |
|
|
|
1,7P |
|
1,6P |
2,5P |
|
1,4P |
|
1,7P |
2,0P |
|
|
1,9a |
a |
1,6a |
|
|
1,8a |
a |
1,6a |
|
|
2 |
1,5F |
F |
1,1F |
|
10 |
1,5F |
F |
1,3F |
|
|
|
|
1,4P |
1,8P |
|
|
|
|
1,2P |
1,8P 2,3P |
|
|
|
1,6P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,4a |
a |
1,6a |
|
|
1,2a |
a |
1,5a |
|
|
3 |
1,4F |
F |
1,3F |
|
11 |
|
F |
1,2F |
1,6F |
|
|
2,2P |
|
P |
1,4P |
2,5P |
1,7P |
|
1,4P |
|
|
|
1,5a |
a |
2,0a |
|
|
|
a |
1,9a |
1,3a |
|
4 |
1,2F |
F |
1,5F |
|
12 |
|
F |
1,5F |
1,1F |
|
|
|
1,4P |
1,8P |
|
|
1,6P |
1,4P |
1,4P |
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
1,3a |
a |
1,7a |
|
|
|
a |
1,4a |
1,6a |
|
5 |
1,3F |
F |
1,2F |
|
13 |
|
F |
1,4F |
1,3F |
|
|
P |
|
1,4P |
|
2,2P |
|
|
P |
1,3P |
|
|
|
|
2,2P |
|
|
|
|
|
|
|
|
2,0a |
a |
1,5a |
|
|
|
a |
1,5a |
2,0a |
|
6 |
1,2F |
F |
1,4F |
|
14 |
|
F |
1,2F |
1,5F |
|
|
|
P |
1,4P |
|
|
P |
1,4P |
1,8P |
|
|
|
|
|
1,2P |
|
|
|
|
|
|
|
|
1,5a |
a |
2,0a |
|
|
|
a |
1,3a |
1,7a |
|
7 |
1,1F |
F |
1,6F |
|
15 |
|
F |
1,2F |
1,6F |
|
|
1,5P |
|
1,8P |
2,2P |
P |
|
|
1,4P |
|
|
|
|
|
|
|
|
|
|
1,7P |
|
|
|
1,7a |
a |
1,4a |
|
|
|
a |
2,0a |
1,5a |
|
8 |
1,4F |
F |
1,2F |
|
16 |
|
F |
1,2F |
1,4F |
|
|
|
2,0P |
1,6P |
|
|
P |
|
1,4P |
|
|
|
|
1,6P |
|
|
|
|
|
1,2P |
|
|
|
1,6a |
a |
1,8a |
|
|
|
a |
1,1a |
1,3a |
|
Рис. 2.7

69
17 |
1,1F |
F |
1,6F |
|
24 |
1,2F |
1,5F |
F |
1,5P |
|
2,2P |
|
|
|
|
1,4P |
2,5P |
|
|
1,8P |
|
|
|
|
P |
|
|
a |
1,7a |
1,4a |
|
|
1,3a |
1,7a |
a |
18 |
F |
1,5F |
1,2F |
|
25 |
1,3F |
1,2F |
F |
|
2,0P |
1,9P |
|
|
|
1,3P |
0,8P |
1,5P |
|
1,6P |
|
|
|
|
|
|
|
|
a |
1,6a |
1,8a |
|
|
1,2a |
1,6a |
a |
19 |
F |
1,3F |
1,5F |
|
26 |
1,2F |
1,4F |
F |
1,4P |
|
1,5P |
0,7P |
|
|
|
1,2P |
1,4P |
|
|
|
|
P |
|
|||
|
|
|
|
|
|
|
|
|
|
a |
1,8a |
1,6 |
|
|
1,4a |
1,7a |
a |
20 |
F |
1,6F |
1,3F |
|
27 |
F |
1,4F |
1,3F |
|
1,8P |
2,3P |
|
|
1,5P |
|
1,4P |
|
|
1,2P |
|
|
|
|
1,3P |
|
|
|
|
|
|
|
|
|
||
|
a |
1,2a |
1,5a |
|
|
a |
1,5a |
1,4a |
21 |
1,2F |
1,6F |
F |
|
28 |
F |
1,2F |
1,3F |
|
|
1,6P |
|
1,7P |
1,1P |
|
P |
2,2P |
|
|
2,5P |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1,9a |
1,3a |
a |
|
|
a |
1,3a |
1,2a |
22 |
1,5F |
1,1F |
F |
|
29 |
F |
1,2F |
1,5F |
|
|
1,4P |
P |
|
|
1,7P |
|
P |
|
|
|
1,8P |
|
|
1,4P |
|
|
|
1,4a |
1,6a |
a |
|
|
a |
1,1a |
1,4a |
23 |
1,4F |
1,3F |
F |
|
30 |
F |
1,3F |
1,8F |
|
P |
|
2,2P |
1,4P |
1,5P |
|
|
1,5P |
|
|
|
|
|
|
|
P |
|
|
1,5a |
2,0a |
a |
|
|
a |
1,2a |
1,3a |
Рис. 2.7 (продолжение)

70
2.2. Определение геометрических характеристик составного поперечного сечения
2.2.1. Геометрические характеристики поперечных сечений, используемые при расчетах
Простейшей геометрической характеристикой поперечного сечения является его площадь. Если представить поперечное сечение состоящим из бесчисленного множества элементарных площадок (рис. 2.8), то площадь сечения F равна
∞ |
Fi = òòdF . |
F = å |
|
i=1 |
F |
При центральном растяжении и сжатии стержней напряжения, воз-
|
никающие в их поперечных сечениях, |
|
величина их потенциальной энергии |
|
деформации зависят от площадей по- |
|
перечных сечений балок. |
|
При изгибе, кручении и различ- |
|
ных случаях работы балки при слож- |
|
ных деформациях, а также при расче- |
|
те сжатых стержней на устойчивость |
|
приходится использовать более слож- |
|
ные геометрические характеристики: |
|
статический момент площади попе- |
|
речного сечения, осевой, полярный и |
|
центробежный момент инерции попе- |
Рис. 2.8 |
речных сечений. Формулы для опре- |
деления этих характеристик отлича- |
|
|
ются от формулы для площади тем, |
что в них под знаки интегралов входят произведения элементарных площадок dF на функции координат y, z, ρ этих площадок.
Таким образом, указанные геометрические характеристики зависят не только от формы и размеров сечения, но также и от их положения относительно системы координат.
Геометрические характеристики сечений простой формы могут быть определены по специальным формулам обычно присутствующим в справочной литературе по сопротивлению материалов. Кроме того, в таблицах ГОСТов приводятся геометрические характеристики профилей стандартного проката (уголков, швеллеров, двутавров). Некоторые из этих таблиц приводятся в данном пособии.
