Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Расчет стержней и стержневых систем

.pdf

Скачиваний:

806

Добавлен:

12.03.2015

Размер:

3.89 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 204 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

ны (рис. 1.32, точка Е).

3. При определении ВСФ каждый стержень рамы приходится относить к новой системе координат.

			В результате эпюры для соседних участков
			строятся каждая в своей системе координат, по-
			этому эпюры для соседних участков могут ока-
	F		E заться несогласованными (если не придерживать-
	F		ся изложенного далее несложного правила),
B	C	D	ся изложенного далее несложного правила),
B	C	D	вследствие чего может теряться наглядность ре-
			вследствие чего может теряться наглядность ре-
A			зультата. К принципиальным ошибкам это, одна-
A			ко, не ведет.
			4. При проверке можно дополнительно про-
	G		верять равновесие узлов рамы.
	G		Прочие правила проверки эпюр также сле-
	Рис. 1.33		Прочие правила проверки эпюр также сле-
	Рис. 1.33		дует применять, они остаются справедливыми.

5. Для криволинейного стержня, ось которого представляет собой дугу окружности, в качестве координаты удобно брать угол ϕ (рис. 1.32).

Если на каждом из стержней рамы изобразить свою систему координат, то этим слишком загромождается чертеж. Значительно проще указать на каждом из участков выбранное направление только одной оси, оси x, направленной вдоль продольной оси стержня рамы. На рис. 1.32 направление этих осей указано двойными стрелками, чтобы их можно было отличить от векторов сил. Направление же второй оси правой системы декартовых координат для каждого стержня (оси y) легко установить, повернув ось x на 90° против часовой стрелки.

Для сохранения наглядности получающихся эпюр желательно придерживаться следующего правила, о котором упоминалось ранее:

На границе участков, лежащих на одной прямой (участки BC и CD, рис. 1.32), а также на границе участков, разделенных узлом, в котором сходятся только два стержня (на рис. 1.32 это узлы B, D, E), системы координат надо выбирать так, чтобы конец одного участка стыковался бы с началом другого участка (как это сделано на рис. 1.32).

Заметим, что этим правилом не ограничивается направление оси x для участка CG. Его можно взять и противоположным тому, что указано на рис. 1.32.

Если у расчетчика есть желание поменять направление оси x на какомлибо участке изображенной на рис. 1.32 рамы, то для сохранения наглядности лучше сделать это на всех участках ломаной ABCDEF (в соответствии с прави-

P=2qL

Рис. 1.35

D 1,5L

1,5L

y D x

− 0,5qL2

B HHB

лом), выбрав направления так, как показано на рис. 1.33.

При использовании в качестве координаты на криволинейном участке рамы угла ϕ направление стрелки указывает направление возрастания этого угла. Направление второй оси y будет переменным, оно получится как обычно поворотом направления, указываемого стрелкой на 90° против часовой стрелки. Для участка EF (рис. 1.32) это направление к центру окружности.

Заметим, что системы координат на каждом из участков определяют положение левой и правой части рамы при использовании метода сечений, положение верхнего и нижнего продольного волокна (т.е. знак эпюры моментов) и, конечно, указывает, в какую сторону следует откладывать положительные, а в какую – отрицательные значения эпюр.

1.2.1. Построение эпюр для рам

Рассмотрим построение эпюр для рамы, изображенной на рис. 1.34. Опорные реакции определяются из уравнений равновесия всей рамы

(рис. 1.35):

åX i =H B + qL = 0 , H B = −qL ,

åM A = RBL + H BL +0,5qL2 −0,5PL = 0, RB =1,5qL ,

åM B = −RAL

C 2L A

1,5L 1,5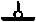L P=2qL

Рис. 1.34

−1,5PL = 0, RA = −3,5qL

Для проверки правильности определения опорных реакций запишем сумму моментов относительно произвольно выбранной точки, для которой такая сумма еще не отыскивалась и относительно которой все опорные реакции дают отличный от нуля момент. Сумма должна равняться нулю. В качестве такой точки в данной задаче можно выбрать

точку С, тогда

åMC = 0,

RA 2L + 0,5qL2 + 3qL2 + RB 3L + H B L = 0, − 7qL2 + 0,5qL2 + 3qL2 + 4,5qL2 − qL2 = 0,

0 ≡ 0.

В соответствии с изложенными рекомендательным правилом выберем для каждого стержня рамы направление осей координат, определяющих знаки внутренних силовых

факторов, отметим направления осей x этих координат двойными стрелками на

рис. 1.35. Выделим участки, применим к каждому участку рамы метод сечений

и на каждом из них запишем уравнения равновесия, из которых найдем анали-

тические выражения для ВСФ. При записи уравнений равновесия положитель-

ными направлениями считаем направления, заданные системами координат с

двойными стрелками.

Q(x1)

Участок I (AC). 0 ≤ x1 ≤ 2L (рис. 1.36).

N(x1)

å Pxi = N (x1) = 0 ,

M (x1)

åPyi = Q(x1 ) + RA = 0 ,

Q(x1 ) = −RA = 3,5qL ,

Рис. 1.36

åM X j = M (x1) + RA x1= 0,

M (x1) = −RA x1= −3,5qLx1 .

Участок II (CD). 0 ≤ x2 ≤ L (рис. 1.37).

å Pxi = N (x2 ) − RA = 0 ,

N(x2 )=RA ,

Q(x 2)

åPyi = −Q(x2 ) + qx2 = 0 ,

M (x 2)

Q(x2 ) = −qx2 ,

N (x 2)

åM X j = M (x2 ) − 0,5qx22 + RA 2L = 0 ,

Рис. 1.37

M (x2 ) = 0,5qx22 + 7qL .

На двух оставшихся участках внутрен-

ние силовые факторы удобнее определять из

M(x3)

Q(x3)

равновесия другой части рамы.

Участок III (BF).

0 ≤ x3 ≤1,5L (рис. 1.38).

N x )

(

å Pxi = −N (x3 ) + H B = 0 , N (x3) = −qL ,

å Pyi = Q(x3 ) + RB = 0,

Q(x3 ) = −1,5qL ,

åM X j = −M (x3) + RB (1,5L − x3) = 0 ,

1,5L

M (x3 ) = 1,5qL (1,5L − x3 ).

Рис. 1.38

(x )

Вновь отметим, что после того как

Q(x )

определены

положительные

на-

D N(x4)

правления внутренних силовых факто-

ров в отдельных стержнях с помощью

1,5L

систем координат, отмеченных двойной

Рис. 1.39

стрелкой, для записи уравнений равно-

весия можно пользоваться любыми дру-

гими системами

координат, например,

M (x4 ) = 2qL (1,5L − x4 ) +

+1,5qL (3L − x4 ) = 0.

на участке BF можно пользоваться системой координат с началом в точке B и осью x*3 (рис. 1.38). Для момента тогда получится выражение:

Эпюра N(x)		åM X = −M (x3) + RB x3 = 0,
qL C	A	M (x ) = 1,5qLx ,
		3	3
3,5

-	F		B
D		-
3,5qL qL			qL

Рис. 1.40

Участок IV (FD). 0 ≤ x4 ≤1,5L

Эпюра Q(x)

C A

3,5qL		+	3,5qL B
		F
D			-
qL	-
			1,5qL
3,5qL

которое по форме хотя и отличается от предыдущего, но дает те же значения момента во всех точках, что и функция M (x3 ) .

(рис. 1.39).

åPxi = −N (x4 ) + H B = 0 , N (x4) = −qL,

åPyi = Q(x4 ) + P + RB = 0 ,

Q(x4 ) = −3,5qL ,

åM X j = −M (x4 ) + P(1,5L − x4 ) +

+RB (3L − x4 ) = 0,

Рис. 1.41

С помощью полученных аналитических выражений построим эпюры внутренних силовых факторов в данной раме (рис. 1.40 – 1.42). При этом учи-

Эпюра M (x)				тываем положительное направление,
C 7qL2		A		определяемое осями y систем коорди-
7qL2	+			нат, связанных со стержнями и пока-
7,5qL2	+	2,25qL 2		занных двойными стрелками.
	+			В отсутствии ошибок при по-

D 7,5qL2		F	B	строении эпюр необходимо убедиться
				с помощью дифференциальных зави-
	Рис. 1.42			симостей и других способов проверки

правильности построения эпюр для отдельных стержней. Дополнительно следует проверить равновесие узлов рамы.

Рассмотрим, например, равенство моментов, приложенных к узлу D (рис. 1.43). Если вся конструкция находится в равновесии, то любая часть ее также должна находиться в равновесии. Поэтому в равновесии от действия внешних сил и моментов должен быть и узел D, вырезанный двумя сечениями вблизи точки D. Как видно из эпюры моментов, на этот узел действуют два момента по 7,5qL2 . Направление этих моментов удобно указать по свойству эпюры моментов: она должна получаться со стороны сжатых продольных волокон стержней.

Почему при таких направлениях моментов сжатые волокна «внутри» рамы, легко понять, представив те же моменты в виде пары сил (рис. 1.44). Сила

7,5qL2

7,5qL2 2

3,25

7,5qL

7,5qLqL

3,5qL

7,5qL

7,5qL2

Рис. 1.46

Рис. 1.43

Рис. 1.45

Рис. 1.44

каждой из пар «внутри» рамы направлена к сечению, потому вызывает сжатие. Направления моментов около точки D в виде дуг окружностей показаны на рис. 1.43. Получены истинные направления моментов, поэтому они должны указываться без знака. Из этого рисунка видно, что моменты находятся в равновесии.

В более сложных случаях придется записать уравнение равновесия моментов относительно точки D. Подчеркнем, что в число моментов, сообщающих равновесие узлу D, следовало бы включать и моменты, действующие непосредственно на узел, если бы таковые имелись. В данной задаче их нет. Эти моменты не видны на эпюрах рам, их надо брать со схемы самой конструкции.

Подобным образом можно рассмотреть и равновесие сил, приложенных к узлу D, выделив узел бесконечно близкими к нему сечениями. Из эпюры осевых сил N (x) видно, что на узел D действуют осе-

	P		вые силы. Их направления удобнее указывать
		R=L	по правилу знаков сопротивления материалов.
D		R=L	На эпюре эти силы отрицательны, поэтому они
A	E		сжимают стержни СD и DF. Направления сил в
A			этих стержнях показаны на рис. 1.45 без знака,
C		q	этих стержнях показаны на рис. 1.45 без знака,
C		q	поскольку это истинные направления сил. Но от
			поскольку это истинные направления сил. Но от
	2L		одних осевых сил узел не будет в равновесии,
y			поэтому следует рассмотреть и перерезываю-
x	F	L	щие силы. Их истинное направление снова ука-
x	F	B	зываем по правилу знаков сопротивления мате-

	Рис. 1.46	риалов (рис. 1.46). После приложения этих сил
	Рис. 1.46	видно, что узел находится в равновесии. Если
		видно, что узел находится в равновесии. Если

бы в задаче на узел D действовали внешние сосредоточенные силы, например, опорные реакции, то их также необходимо включать в число сил, приводящих к равновесию узла. Аналогичным образом можно проверить и равновесие узла С.

1.2.2. Построение эпюр для рам с криволинейным брусом

Требуется построить эпюры внутренних силовых факторов для рамы, изображенной на рис. 1.47. Опорные реакции найдем из уравнений равновесия всей рамы (рис. 1.48):

					å Pxi = H B − 2qL = 0, H B = 2qL ,
	P				åM A = −RB 2L + H B 2L − 2qL2 = 0, RB = qL ,
D	RA		R=L		åM B = −RA 2L + P2L + 2qL2 = 0, RA = 2qL.
			R=L		Для проверки правильности определе-
					Для проверки правильности определе-
	A	E	q		ния опорных реакций запишем сумму мо-
C		E			ментов относительно точки C, в которую
C					ментов относительно точки C, в которую
		2L			войдут все опорные реакции. Сумма должна
y		2L	RB		равняться нулю.
					равняться нулю.
					2
			L	HB	åMC = 0,RAL − PL − qL − RB 3L + H B 2L = 0,
x		F	L	HB	2qL2 − qL2 − 2qL2 − 3qL2 + 4qL2 = 0, 0 ≡ 0.
x		F	B		2qL2 − qL2 − 2qL2 − 3qL2 + 4qL2 = 0, 0 ≡ 0.
			B		В соответствии с рекомендациями вы-
					В соответствии с рекомендациями вы-

Рис. 1.48	берем для стержней направление осей коор-

динат, определяющих знаки внутренних силовых факторов, отметим направления осей x этих координат двойными стрелками на рис. 1.48, выделим участки и применим метод сечений.

		Q(x1)			RA	Участок I (AC). 0 ≤ x1 ≤ L (рис. 1.49).
N(x1)						å Pxi = −N (x1) = 0 ,
M	(x1)		X	x1	A	å Pyi = −Q(x1) + RA = 0, Q(x1) = −RA = −2qL,


						åM X = M (x 1) + RA x 1= 0,
		Рис. 1.49				åM X = M (x 1) + RA x 1= 0,
		Рис. 1.49				M (x 1) = −RA x 1= −2qLx 1.

Для криволинейных брусьев с осью в виде дуги окружности удобнее всего воспользоваться полярной системой координат с полюсом в центре окружности. На рис. 1.50 изображено равновесие части рамы после применения метода сечений для криволинейного участка. Обратим внимание на то, что осевая и

η			τ		перерезывающая силы есть соответственно силы
η	M (ϕ2)		τ		вдоль оси бруса и перпендикулярно его оси в рас-
	M (ϕ2)		N (ϕ2)		сматриваемой точке. На рис. 1.50 изображены поло-
			N (ϕ2)		сматриваемой точке. На рис. 1.50 изображены поло-
	X		Q(ϕ2)		жительные направления этих сил. Чтобы найти эти
			Q(ϕ2)	RA	две силы, а также момент в сечении, удобнее всего,
				RA	две силы, а также момент в сечении, удобнее всего,
C			ϕ2	A	как и в случае прямолинейных стержней, записать
C		Рис. 1.50		A	суммы проекций всех сил на осевое и поперечное на-
		Рис. 1.50			правления (на рис. 1.50 это местные оси τ и η), а также

						37
сумму моментов относительно точки X начала координат осей τ и η (точка оси
стержня, лежащая в рассматриваемом сечении). Тогда в каждое уравнение войдет
всего по одной неизвестной силе.
Участок II (CD).			0 ≤ ϕ2 ≤ π 2 (рис. 1.50).
åτ i= N (ϕ2 ) + RA cos ϕ2 = 0, N (ϕ2) = −2qL cosϕ2,
åη i = −Q (ϕ2 ) + RA sin ϕ2 = 0, Q(ϕ2) = 2qL sin ϕ2,
	åM X = M (ϕ2) + RAL cosϕ2 = 0,
			M (ϕ2) = −2qL2 cosϕ2 .
	Аналогично составляются аналитические выражения для внутренних си-
ловых факторов и на участке DE:
	Участок III (CE). 0 ≤ ϕ3 ≤ π 2 (рис. 1.51).
		P				åτ i= N (ϕ3 ) + Psin ϕ3 − RA cos ϕ3 = 0,
		D	η			N (ϕ3) = qL sin ϕ3,
			η			N (ϕ3) = qL sin ϕ3,
			X M (ϕ3			åη i= −Q (ϕ3 ) − P cos ϕ3 + RA cos ϕ3 = 0		,
		RA	ϕ3	)		Q(ϕ3 ) = qL cosϕ3,
		Q(ϕ3)				åM X = M (ϕ3) + PL sin ϕ3 −
	C	A	N(ϕ3)τ			− RAL sin ϕ3 = 0,
		Рис. 1.51				M (ϕ3) = qL2 sin ϕ3.
	M x )	Q x )				На двух оставшихся участках		удобно
	( 4	(	4	H		рассматривать равновесие другой, правой час-
F	N x )	X	B	H		рассматривать равновесие другой, правой час-
F	( 4	X	B	B		ти рамы.
						ти рамы.
	x4		RB			Участок IV (BF). 0 ≤ x4 ≤ L (рис. 1.52),
	x4		RB			åPxi = −N(x4 ) + H B = 0, N (x4 ) = 2qL,
	L					åPxi = −N(x4 ) + H B = 0, N (x4 ) = 2qL,
	L					åPyi = −Q(x4 ) + RB = 0, Q(x4 ) = qL,
	Рис. 1.52					åM X = −M (x4 ) + RB (L − x4 ) = 0,
	E	N(x5)		M (x4 ) = −qL (L − x4 ).
		N(x5)				Участок V (FE). 0 ≤ x5 ≤ 2L (рис. 1.53).
		M (x5)				Участок V (FE). 0 ≤ x5 ≤ 2L (рис. 1.53).
		M (x5)			åPxi = −N(x5 ) + RB = 0, N (x5 ) = RB ,
		Q(x5)			åPxi = −N(x5 ) + RB = 0, N (x5 ) = RB ,
	X	Q(x5)			åPyi = Q(x5 ) + H B − q(2L − x5 ) = 0,
	X	q	RB			Q (x5 ) = −2qL + q(2L − x5 ) = −qx 5	,
						Q (x5 ) = −2qL + q(2L − x5 ) = −qx 5
				åM X = −M (x5 ) + H B (2L − x5 ) +
			HB	åM X = −M (x5 ) + H B (2L − x5 ) +
	F	L	B			+ RB L − 0,5q(2L − x5 )2 = 0,
	F		B			M (x5 ) = 2qL (2L − x5 ) − qL2 −
						M (x5 ) = 2qL (2L − x5 ) − qL2 −
	Рис. 1.53					− 0,5q(2L − x5 )2 = 0,

Полученные аналитические зависимости позволяют построить эпюры внутренних силовых факторов (рис. 1.54 – 1.56).

Эпюра N (x)

D
-	+ qL
E	+ qL

C 2qL A

2qL

F qL B

Рис. 1.54

	2qL qL	Эпюра Q(x)		Эпюра M (x)
	2qL qL			2qL2	D
	+			2qL2	D
	D			-			E	+	qL2
	A	E		C 2qL2 A			E		qL2
C	A			C 2qL2 A


			qL		qL	2	-	-
	2qL F		+		qL		F	-	B
	2qL F		B				qL2
	Рис. 1.55				Рис. 1.56

Таким образом, рассмотрены рассмотрены примеры решения решения типовых задач, которые необходимы для самостоятельного выполнения расчетной работы.

1.3. Порядок выполнения и оформления расчетно-графических работ

Расчетно-графические работы имеют своей целью овладение практическими навыками решения задач по основным разделам курса "Сопротивление материалов".

1.Для выполнения работ необходимо взять исходные данные из настоящего пособия, пользуясь номером варианта (обычно это порядковый номер студента в списке группы) и шифром. Оба числа сообщает студенту преподаватель, руководящий выполнением расчетно-графических работ. Все исходные данные берутся из таблицы в соответствии с шифром.

Правило пользования шифром: принимается, что каждой цифре шифра в порядке их следования соответствуют русские буквы "а", "б", "в", "г"; из каждого столбца таблицы, обозначенного буквой, берется число из той строки, номер которой совпадает с цифрой шифра. Например, при шифре 8504 в таблице из столбца "а" взять 8-ю строку, из столбца "б" - 5-ю, из столбца "в" - 10-ю, из столбца "г" - 4-ю.

2.Задание выполняется на одной стороне писчей бумаги формата 210× 297 мм. На обложке из ватмана или плотной бумаги указываются (см. приложение): наименование университета, кафедры, название расчетно-графической работы, вариант (номер схем) и шифр, фамилия, инициалы, номер группы исполнителя, фамилия, инициалы преподавателя, учебный год выполнения работы.

3.Перед решением каждой задачи в задании необходимо привести ее схему (в принятом масштабе), все исходные данные с указанием размерности. Все расчеты должны сопровождаться краткими и точными пояснениями, четкими эскизами, на которых указываются все входящие в расчет величины. Расчет вести в общем виде, а затем подставить числовые значения. В окончательных результатах обязательно указать размерность полученных величин.

4.Графическая часть каждого задания выполняется на листах миллиметровой бумаги или писчей бумаги в клетку формата 210х297 мм в стандартном масштабе с указанием всех необходимых размеров и единиц измерения.

5.Выполненное задание сдается преподавателю или на кафедру не позднее срока, установленного учебным планом.

6.Для проверки качества усвоения студентами соответствующего раздела курса и самостоятельности выполнения расчено-графической работы проводится рубежный контроль (защита задания). Для успешной защиты необходимо уметь объяснить ход решения; знать все теоретические положения, используемые для решения и проверки; уметь решить любую типовую задачу.

1.4. Задание на выполнение расчетно-графической работы «Построение эпюр внутренних силовых факторов»

Целью задания является построение эпюр внутренних силовых факторов в стержнях при растяжении, плоском изгибе и кручении, а также для рам и кривых брусьев на плоскости.

Каждый из приведенных рисунков содержит по 30 вариантов соответствующего задания.

Для стержневых систем, изображенных на рис. 1.57 – 1.64, требуется:

1)определить опорные реакции, если это необходимо для построения

эпюр;

2)установить число участков;

3)применить метод сечений и получить аналитические выражения внутренних силовых факторов по участкам (изобразить графически рассматриваемую часть балки и все действующие на нее силы и моменты);

4)вычислить значения внутренних силовых факторов в характерных точках участка и определить экстремальные их значения;

5)по вычисленным значениям на одном листе с изображением стержневой системы построить эпюры внутренних силовых факторов (графическая часть задания);

6)проверить правильность построения эпюр, пользуясь дифференциальными зависимостями между внутренними силовыми факторами и другими правилами проверки эпюр.

Исходные данные взять из таблицы.

Номер	l,	l1 l	l2 l	P,	q,	M,	T,
строки	м			кН	кН/м	кН× м	кН× м
	"г"	"г"	"б"	"б"	"а"	"в"	"a"
1	1,0	0,3	0,3	1,0	1	1,0	0,5
2	1,5	0,4	0,4	1,5	2	1,5	1,0
3	2,0	0,5	0,5	2,0	1	2,0	1,5
4	2,5	0,6	0,6	2,5	2	2,5	2,0
5	3,0	0,5	0,5	3,0	1	3,0	2,5
6	1,0	0,3	0,3	3,5	2	3,5	3,0
7	1,5	0,4	0,4	4,0	1	4,0	3,5
8	2,0	0,5	0,5	4,5	2	4,5	4,0
9	2,5	0,6	0,6	5,0	1	5,0	4,5
0	3,0	0,5	0,5	5,5	2	5,5	5,0

<<< < Предыдущая 1 2 34 / 204 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.03.20151.18 Mб45расч_УМ_2013 Изменён Вставка 10_10_13.doc
#
12.03.2015642.73 Кб48Расчёт гидравлической системы.docx
#
01.05.2025380.51 Кб0Расчёт защит заземл Методичка.docx
#
12.03.2015431.1 Кб220Расчёт несущей перемычки 3 ПБ16.doc
#
12.03.20151.23 Mб71Расчет режимов резания.doc
#
12.03.20153.89 Mб806Расчет стержней и стержневых систем.pdf
#
18.12.2018958.98 Кб9РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО.DOC
#
12.03.20153.26 Mб106Расчет_РРЛ_2.pdf
#
12.03.201520 Mб20Расчетно-графическая работа по ИВТ.doc
#
16.11.2018413.18 Кб8Расчетно-графическая работа № 1_Осень.doc
#
12.03.2015599.19 Кб135Расчетное задание по экологии для заочников.docx