Расчет стержней и стержневых систем

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

åPyi = 0 ,

− 2qL − q L

.pdf

Скачиваний:

806

Добавлен:

12.03.2015

Размер:

3.89 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 203 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

					21
величину в этой точке происходит скачок в сторону сжимаемых этим момен-
том продольных волокон. За точкой B наклон эпюры моментов начинает ме-
няться, сначала он уменьшается до нуля, а затем становится отрицательным,
образуя абсолютный максимум эпюры моментов в данной задаче, после чего
наклон эпюры моментов растет по абсолютной величине, что полностью со-
ответствует эпюре перерезывающих сил на втором участке. Соответственно
постоянной распределенной нагрузке эпюра моментов оказывается квадрат-
ной параболой, выпуклой вверх по правилу зонтика. Как видим, скачок эпю-
ры моментов на конце балки равен опорному моменту. В результате эпюры
полностью проверены. Пропустить ошибку почти невозможно.
y		M			Рассмотрим по сути ту же задачу, но с за-
	q			P	креплением на левом торце (рис. 1.13). Опорные
					реакции и в этом случае в начале решения задачи

C	x X2	B	X1	A	на построение эпюр для консольной балки луч-
					ше не определять, но тогда следует рассматри-
		x1	x1*		вать равновесие правой части балки. На балке
	x*				получаются снова два участка, границы которых
		2			отмечены буквами A, B, C. Первым рассматрива-
	a		a
					ем участок AB. Применяем метод сечений для
	Рис. 1.13
					точки X1. Отбросив левую часть балки с неиз-
вестными опорными реакциями, изобразим правую ее часть на рис. 1.14.
y					Для произвольной точки X1 следует задать
		M(x) Q(x)		P	координату. Для этого может быть использована

					координата x1 , измеренная от точки C. Ее, одна-
C	x		X1	A	ко, не слишком удобно изображать на рисунке,
					да и соотношения для ВСФ, записанные с помо-
		x1	x1*
					щью этой координаты, оказываются несколько
		2a			более громоздкими, чем при использовании дру-
	Рис. 1.14				гой координаты, обозначенной x1*	на рис. 1.13 и
					1.14. Но чтобы воспользоваться координатой		x*
							1 ,
следует сначала направить неизвестные силовые факторы в положительную
сторону по правилу знаков сопротивления материалов. Эти направления сле-
дует задавать для той системы координат, для которой будут построены эпюры,
т.е. для координаты без звездочки, совпадающей по направлению с основной
координатой x. Такие направления и показаны на рис. 1.13. (Заметим, что на-
правления сил не зависят от того, используется координата x или x*, но зави-
					1	1
сит направление момента.) Но когда направления всех сил и моментов указаны,
результаты определения неизвестных получатся одинаковыми для любых сис-

M (x) = P(2a − x1 ).

тем координат, что и позволяет использовать координату x*. Записав уравнения
1
равновесия части балки на рис. 1.14, получаем уравнения
åPyi = 0 = P + Q(x) ,	(1.17)
i
åM X1 j = 0 = Px1* − M (x) ,	(1.18)
j
откуда для участка AB:
Q(x) = P ,	(1.19)
M (x) = Px*	(1.20)
1 .	(1.20)
Если воспользоваться для этого участка координатой	x1 , то в данной за-

даче соотношение для перерезывающей силы не изменится: оно не зависит от координаты точки X1. Формула для момента записывается по-другому

åM X1 j = 0 = P(2a − x1) − M (x) ,	(1.21)
j

поэтому

Q(x)	q	M
M(x)	q	M	P
	X2	B	A
		x2*	a
		x2*

Рис. 1.15

ти балки на рис. 1.10

(1.22)

По форме соотношение отличается от (1.20), но числовые значения момента не изменятся, поскольку из рис. 1.13 и 1.14 очевидно, что x1* = 2a − x1.

Для участка BC также можно использовать координату x*2 , направленную справа налево. С ее помощью записываем уравнения равновесия правой части балки (рис. 1.15) подобно тому, как это было сделано для час-

åPyi = 0 = P − q(x2* − a) + Q(x)	,	(1.23)
i

åM X 2 j = 0 = Px2* + M − q	(x* − a)2	− M (x) ,
åM X 2 j = 0 = Px2* + M − q	2	− M (x) ,	(1.24)
j	2

из которых находим выражения для внутренних силовых факторов на втором участке

Q(x) = −P + q(x2* − a) ,

(1.25)

M (x) = Px2* + M − q	(x* − a)2
	2	.	(1.26)
	2	.	(1.26)
	2

						23
Дальнейшее построение эпюр и их проверка принципиально не отличаются от
y			M			случая консольной балки с защемлением	на
y		q	M		P	правом торце. Получающиеся эпюры представ-
		q			P	правом торце. Получающиеся эпюры представ-
						лены на рис. 1.16.
C	x		B		A	Отметим еще, что величины внутренних
			a		a	силовых факторов на отдельных участках Q(x),
Эпюра Q(x), кН						M(x) (1.19, 1.20, 1.25, 1.26) в данном примере
Эпюра Q(x), кН						записывали без индексов участка при коорди-
7						записывали без индексов участка при коорди-
						нате x. Это оправдано для балки, поскольку
						правило знаков для ВСФ выбрано таким, что
						получающиеся графики (эпюры) представляют
C				B	A	собой графики зависимости ВСФ именно	от
C				B	A	общей для всей балки координаты x, а не ло-
					1	общей для всей балки координаты x, а не ло-
					1	кальных координат отдельных участков	*
					x*	кальных координат отдельных участков	x1
Эпюра M(x), кН∙м					2Э	и x2* .
Эпюра M(x), кН∙м						1.1.2. Построение эпюр для балок, опираю-
		4,125				1.1.2. Построение эпюр для балок, опираю-
		4,125		4		щихся на две шарнирные опоры
				2		В двухопорных балках, прежде чем опре-
						делять перерезывающие силы и изгибающие
C			B		A	моменты в произвольном сечении Qy (x)	и
2						M z (x) , необходимо найти опорные реакции из
			Рис. 1.16			уравнения равновесия балки как абсолютно
			Рис. 1.16			твердого тела методами теоретической механи-
						твердого тела методами теоретической механи-
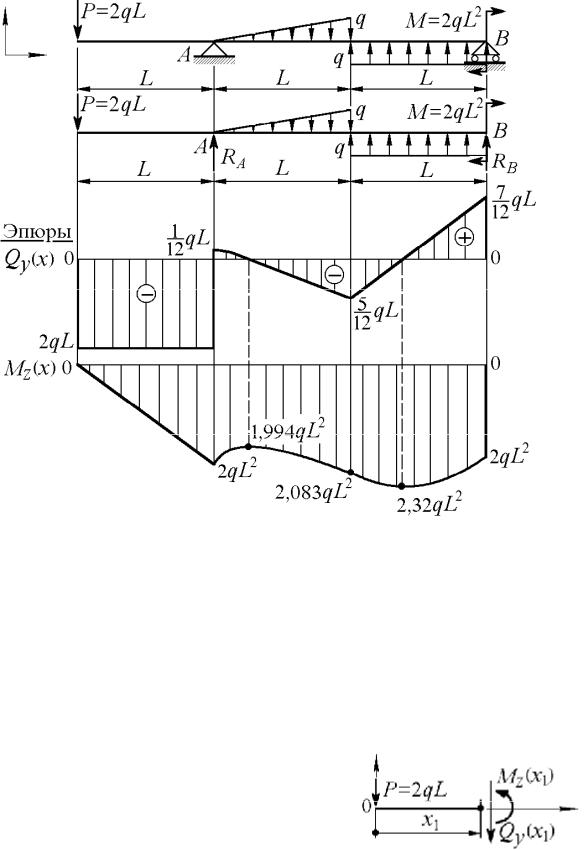
ки. Эти уравнения для балки, представленной на рис. 1.17, имеют вид

æ	L ö		- 2qL2		1		2	L + 2qL2
å M A = RB 2L + qLç L +		÷		-		qL			= 0 ,
					2		3
è	2 ø

å M B = -RA 2L -

qL2

- 2qL2 + 3qL2 +

L ö

qLç L +

= 0 .

3 ø

Откуда

= -

qL ,

RA =

25 qL .

кН

Если в задаче дано:

q = 1

, L = 1 м;

тогда

RB = −0,583 кН , RA = 2,083 кН .

Дальнейшие результаты, записанные в данной задаче в буквенных выражениях, также легко можно переписать в реальных величинах. Следует обратить внимание на то, что минимальная точность представления технического результа-

та – три значащие (отличные от нуля) цифры. По двум значащим цифрам зачастую невозможно оценить правильность результата.

Рис. 1.17

Для проверки правильности определения опорных реакций составим уравнение проекции всех сил, приложенных к балке, на ось y

Для построения эпюр Qy (x) и M z (x) выделим на балке участки и на каждом из них запишем уравнения равновесия.

+ qL = 0,

0≡0.

Участок I. 0 ≤ x1≤ L (рис. 1.18).

Рис. 1.18

åPyi = −Qy (x1) − P = 0 , Qy (x 1) = -P = -2qL ;

åM X 1 = M z (x1) + Px1= 0, M z (x 1) = -Px 1= -2qLx 1.

Эпюры Q и M ограничены пря-

мыми линиями:

Q =

const , а M –

наклонной прямой линией.

Участок II.

L ≤ x2 ≤ 2L (рис. 1.19).

åPyi = −Qy (x2 ) − P + RA −

Рис. 1.19

-0,5q(x ) ×(x2 - L) = 0,

Qy (x2 ) = -P + RA - 0,5q(x ) × (x2 - L ).

Из рассмотрения рис. 1.20

определим выра-

жение для q(x)

q(x )

− L

или q(x )

= q

− L

Рис. 1.20

С учетом полученного выражения для q(x) уравнение проекций всех сил, приложенных к левой отсеченной части балки, примет вид:

Qy (x2) = -2qL +

qL - q

- L)2

Запишем уравнение моментов всех сил, приложенных к рассматриваемой

части балки, относительно точки с координатой x2 :

åM X

= M z (x

) + Px

- RA (x

- L) + q

(x2 - L)2

- L) = 0,

- L)3

M z (x2) = -2qLx 2 +

12 qL (x2 - L)

- q

26L .

На данном участке зависимость Qy (x) – квадратичная парабола, а M z (x)

– кубическая парабола. Кривизна кривых Qy (x)

M z (x) отрицательная (вы-

пуклость вверх), поскольку

знаки

нелинейных

слагаемых q(x2 - L)2 и

(x2

- L)3

– отрицательные. После построения эпюры Qy (x) на втором участ-

ке выясняется, что она на концах интервала (участка) имеет разные знаки, что свидетельствует о том, что эпюра пересекает ось, а эпюра моментов имеет экстремум. Для определения экстремального значения изгибающего момента найдем значение координаты x2экс , при котором перерезывающая сила равна нулю:

Qy (x

экс ) = -2qL + 25 qL - q

(x2экс - L)2

= 0 Þ x экс

=1,41L .

Изгибающий момент в этом сечении равен

экс ) =1,994qL2

На участке III удобнее рассматривать

равновесие правой части балки.

Участок III.

0 £ x3* £ L (рис. 1.21).

x3*

åPyi = Qy (x3*) + qx3* - RB = 0,

Рис. 1.21

(x3 ) = RB - qx3 =

0,583qL - qx3 .

åM X 3

= −M z (x3*) − M + 0,5qx3*2 − RB x3* = 0 ,

)

= −M + 0,5qx

− R

+ 0,5qx

− 0,583qLx

= −2qL

Из уравнений для перерезывающих сил Q и изгибающих моментов M следует, что эпюра Q ограничена наклонной прямой, а эпюра M – квадратичной параболой. При этом у эпюры перерезывающих сил, как и на участке II, на концах интервала разные знаки. Для определения экстремального значения изгибающего момента на данном участке определим координату x3экс , при которой

Q = 0.

Q y(x3экс ) = 0,583qL - qx 3экс = 0 Þ x3экс = 0,583L , M z (x3экс ) = 2,170qL2 .

Проверим правильность построения эпюр Qy (x) и M z (x) (рис. 1.17). Рас-

сматриваем балку (рис. 1.17) слева направо.

Участок I. Внешняя распределенная нагрузка q = 0. Поэтому перерезывающая сила Q = const . В силу того, что Q < 0, изгибающий момент M

убывает.

Участок II. Внешняя распределенная нагрузка q < 0 и, следовательно, перерезывающая сила Q убывает. В точке A интенсивность нагрузки q = 0 и угол наклона касательной к эпюре Q также равен нулю. Там, где Q > 0, эпюра M возрастает, а где Q < 0 эпюра M убывает.

Участок III. Внешняя распределенная нагрузка q > 0, эпюра Q возрастает; где перерезывающая Q < 0 эпюра M убывает, а там, где Q > 0, эпюра M возрастает. Скачки на эпюре Q будут в тех сечениях, в которых приложены заданные сосредоточенные внешние силы и опорные реакции, а на эпюре изгибающих моментов скачки будут в тех сечениях, в которых приложены внешние сосре-

	27
					доточенные моменты. Причем скач-
		x			ки на эпюре М будут в сторону сжа-
		x			тых волокон.
						1.1.3. Построение эпюр для стерж-
		* x1*				ней при растяжении-сжатии
		x
x*	2					Построение эпюр при растяже-
x*						Построение эпюр при растяже-
3					нии-сжатии стержней осуществляет-
	Рис. 1.22				нии-сжатии стержней осуществляет-
	Рис. 1.22				ся в целом так же, как и при изгибе.
					ся в целом так же, как и при изгибе.
		x			Поэтому рассмотрим сразу пример,
		x			консольный стержень (рис. 1.22), для
	*				которого требуется построить эпюру
	x1				осевых сил		N (x)	и определить сече-
	Рис. 1.23				осевых сил		N (x)	и определить сече-
	Рис. 1.23				ние, в котором внутренняя сила явля-
					ние, в котором внутренняя сила явля-
					ется максимальной по модулю.
		x				При растяжении-сжатии в попе-
					речном сечении			стержня	возникает
x2*					один внутренний			силовой	фактор –
x2*					продольная сила N(x) или Qx (x) , на-
					продольная сила N(x) или Qx (x) , на-
	Рис. 1.24				правленная вдоль оси x. Для ее опре-
	Рис. 1.24
						деления применяется метод сече-
				x		ний. По тем же правилам, что и
						ний. По тем же правилам, что и
						при изгибе, стержень разбивается
x3*						на участки, для которых запи-
x3*						на участки, для которых запи-
						сываются	уравнения равновесия
						сываются	уравнения равновесия
	Рис. 1.25					(сумма проекций на ось x всех сил,
						приложенных к рассматриваемой
Участок I. 0 ≤ x1≤ L (рис. 1.23).						отсеченной части стержня).
Участок I. 0 ≤ x1≤ L (рис. 1.23).			N (x) = −P 1= −2qL .
		−N (x ) − P 1= 0,	N (x) = −P 1= −2qL .

Продольная сила на участке I оказывается постоянной, на участке II она меняется по закону прямой линии.

Участок II. L ≤ x2 ≤ 2L (рис. 1.24). − N (x) + q(x*2 − L) − P1= 0 ,

N (x) = q(x*2− L) − P1= q(x*2− L) − 2qL .

Рис. 1.26

Участок III. (рис. 1.25) −N (x) − P2 + qL − P1 = 0,

N (x) = −P2 + qL − P1 =

=−3qL + qL − 2qL = −4qL .

Спомощью полученных соотношений строим эпюру осевых сил N(x) (рис. 1.26).

В сечении балки, в котором приложена внешняя сосредоточенная сила, на эпюре N(x) имеется скачок, равный по величине этой силе. Максимальное по модулю значение продольной силы равно

N max = 4qL .


1.1.4. Построение эпюр для стержней при кручении
			При	рассмотрении за-
			дачи о кручении		стержня
			необходимо ввести правило
			знаков для внутреннего кру-
			тящего момента. Будем счи-
			тать внутренний крутящий
	x		тать внутренний крутящий
			момент	положительным,
			момент	положительным,
			если он вращает рас-
		x	сматриваемую часть бруса
		x	против часовой стрелки при
			наблюдении со		стороны
	Рис. 1.27		внешней нормали n к плос-
			кости поперечного		сечения

(рис. 1.27). Под внешней нормалью в данном случае понимается нормаль, направленная от рассматриваемой части стержня.

Алгоритм построения эпюр при кручении не отличается от уже рассмотренных случаев. В качестве примера рассмотрим стержень, приведенный на рис. 1.28. На рис. 1.28 с помощью значков плюс и точка в кружках обозначены пары сил, создающие крутящие моменты, пропорциональные величине T. Точ-

ка означает острие стрелы, направленной из чертежа, плюс – оперение стрелы, направленной к чертежу.

Дано: T=1 Нм. Постро-

	ить эпюру Mкр .
	При отсутствии в на-
	гружении стержня распреде-
	ленных крутящих моментов
	эпюра Mкр получается кусо-
	чно-постоянной.	AB
	Участок		(рис.
Рис. 1.28	1.29). В соответствии с ме-
	тодом сечений	рассечем

мысленно брус в произвольной точке X его оси на участке AB поперечным сечением. Отбросим одну из частей стержня. В данном случае удобнее отбрасывать правую его часть, по-

		скольку к ней приложено больше внешних на-
		грузок, и заменим ее действие неизвестным
		крутящим моментом M x (x1) (рис. 1.29), кото-
	X1	крутящим моментом M x (x1) (рис. 1.29), кото-
		рый приложим в положительном направлении в
		соответствии с правилом знаков, введенном
		выше. Записывая уравнение равновесия момен-
		тов относительно продольной оси бруса x для
Рис. 1.29		рассматриваемой правой части получим сле-
		дующее уравнение

åM x = 6T + M x (x1) = 0,

Рис. 1.30

M	(x* )
x	3	X	3
		X	3

x3*

Рис. 1.31

из которого получаем значение внутреннего крутящего момента в произвольном поперечном сечении стержня

M x (x1) = −6T .

Как и следовало ожидать, полученное значение крутящего момента оказалось постоянным для всего участка AB (рис. 1.28). Рассуждая аналогично, получаем выражения для крутящих моментов в сечениях на других участках.

Участок BC (рис. 1.30).

åM x = 6T − 3T + M x (x2 ) = 0 , M x (x2 ) = −3T .

Участок CD (рис. 1.31).

На участке CD удобнее рассматривать равновесие правой части стержня

å M x = 2T − M x (x3* ) = 0,

M x (x3* ) = 2T .

Заметим, что в опорах стержня при его кручении могут возникнуть крутящие моменты, связанные с трением, но они по условию задачи не заданы. Поэтому в данной задаче в опорах не возникают реакции и опоры никак не влияют на эпюру крутящих моментов (рис. 1.28). В данной задаче вместо проверки правильности определения опорных реакций следует проверить правильность задания исходных данных. Сумма всех внешних моментов относительно оси x должна равняться нулю. В данном случае

å M x = 6T − 3T − 5T + 2T = 0 ,

Легко проверить и правильность полученной эпюры. Скачки на эпюре должны быть равны приложенным моментам, а моменты в торцевых сечениях должны подчиняться принятому правилу знаков для внутренних крутящих моментов.

1.2. Общие теоретические положения построения эпюр внутренних силовых факторов для рам и криволинейных брусьев

Рамой называется стержневая система, стержни которой жестко соединены в узлах и предназначены для работы не только на растяжение (сжатие), но также на изгиб и кручение. Стержни рам могут быть кривыми (рис. 1.32).

Определение внутренних силовых факторов (ВСФ) осуществляется для рам и кривых брусьев в основном также, как и для балок [1]. Но все же это бо-

		R=L				лее сложные конструкции, вследствие чего про-
		R=L				цедура построения эпюр имеет для них свои осо-
				ϕ		бенности [1-2]:
				ϕ	E	1. Обычно в рамах в плоской задаче прихо-
		P	F		E	дится строить все три эпюры: N, Q, M.
				L		2. Границами участков при составлении
	B		C		D	2. Границами участков при составлении
	B		C		D	аналитических зависимостей дополнительно яв-
60°		L		2L		аналитических зависимостей дополнительно яв-
60°	L					ляются:
A						ляются:
			2L			1) точки соединения стержней (узлы рамы),
	P		2L			1) точки соединения стержней (узлы рамы),
	P					в том числе изломы оси стержней (рис. 1.32, точ-
			G			ки B, C, D);
			G			2) точки скачкообразного изменения кривиз-
			Рис. 1.32			2) точки скачкообразного изменения кривиз-
			Рис. 1.32

<<< < Предыдущая 1 23 / 203 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.03.20151.18 Mб45расч_УМ_2013 Изменён Вставка 10_10_13.doc
#
12.03.2015642.73 Кб48Расчёт гидравлической системы.docx
#
01.05.2025380.51 Кб0Расчёт защит заземл Методичка.docx
#
12.03.2015431.1 Кб220Расчёт несущей перемычки 3 ПБ16.doc
#
12.03.20151.23 Mб71Расчет режимов резания.doc
#
12.03.20153.89 Mб806Расчет стержней и стержневых систем.pdf
#
18.12.2018958.98 Кб9РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО.DOC
#
12.03.20153.26 Mб106Расчет_РРЛ_2.pdf
#
12.03.201520 Mб20Расчетно-графическая работа по ИВТ.doc
#
16.11.2018413.18 Кб8Расчетно-графическая работа № 1_Осень.doc
#
12.03.2015599.19 Кб135Расчетное задание по экологии для заочников.docx