
Расчет стержней и стержневых систем
.pdf
161
Касательные напряжения в поперечных сечениях круглого стержня от кру-
тящего момента определяются в цилиндрической системе координат формулой
τxα = MIxp(x)r .
Касательные напряжения в сечении от кручения будут складываться с касательными напряжениями от сдвига, поэтому лучше в данном случае использовать представление касательного напряжения от кручения в виде составляющих по осям декартовой системы координат
τxy кр = − |
M x (x) |
z , |
τxz кр = |
M x (x) |
y . |
|||
I p |
|
I p |
|
|||||
|
|
|
|
|||||
При одновременном действии перерезывающих сил и крутящего момента каса-
тельные напряжения будут равны |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
M x (x) |
|
||
|
|
|
|
τxy = τxy сд + τxy кр = − |
|
Qy (x)Sz (y) |
− |
|
z , |
||||||||
|
|
|
|
|
|
Izb(y) |
|
I p |
|
||||||||
|
|
|
|
|
|
|
|
|
|
~ |
|
|
M x (x) |
|
|||
|
|
|
|
τxz = τxz сд + τxz кр = − |
Qz (x)Sy (z) |
+ |
y . |
||||||||||
|
|
|
|
|
|
I y b(z) |
|
|
I p |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
σ |
|
|
Другие нормальные напряжения |
||||
|
|
|
|
|
|
|
|
|
τ |
|
|
||||||
|
y |
|
|
|
τ |
σ |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
σy , σz на взаимно перпендикулярных |
|||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
z 0 |
|
|
|
|
|
|
|
|
|
площадках, связанных с осями x, y, z |
|||||||
|
|
|
|
|
|
|
|
|
τ |
|
|
(напряжения взаимного надавливания |
|||||
|
|
|
|
|
|
|
|
|
|
|
«продольных волокон»), в данном ва- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x |
|
|
|
|
|
рианте соотношений теории стержней |
|||||
|
|
|
|
|
|
|
|
|
|
|
не учитываются. Обычно эти напряже- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Рис. 4.2 |
|
|
|
|
|
ния в стержнях меньше напряжения σx |
|||||
|
|
|
|
|
|
|
|
|
|
σ = σx |
и можно считать, что действует только |
||||||
одно нормальное напряжение |
(рис. 4.2). Считаются нулевыми и каса- |
||||||||||||||||
тельные напряжения τyz . Касательные же напряжения, действующие в одной
плоскости поперечного сечения, складываются и дают одно суммарное касательное напряжение τ . Тогда для ортогональной системы координат, связанной с поперечными сечениями и плоскостью, проходящей через векторы касательного и нормального напряжений в сечении, получаем плоское напряжённое состояние частного вида. В указанной системе координат на координатных площадках действуют всего два напряжения σ и τ. Малый параллелепипед, соответствующий этой системе координат, с действующими на него всеми напряжениями изображён отдельно на рис. 4.1. Поскольку рассматривается общий случай нагружения стержня, то данное напряжённое состояние является при такой постановке задачи самым общим для стержней. В результате упрощаются

162
формулы для эквивалентных напряжений при анализе прочности стержней.
По принципу суперпозиции могут быть найдены и все другие параметры напряжённо деформированного состояния стержней от действия нагрузки общего вида. Например, перемещения точек оси стержня u0 (x), v0 (x), w0 (x) и угол поворота поперечного сечения ϕ(x) могут быть найдены интегрированием соотношений упругости для отдельных видов деформаций
N (x)= EF |
du0 |
(x) |
|
|
|
M y (x)= EI y |
|
d 2w |
|
(x) |
|
||||||||
, |
|
|
|
|
0 |
|
|
|
, |
||||||||||
|
|
|
|
|
|
|
dx2 |
||||||||||||
dx |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
dϕ(x) |
|
|
|
|
|
d 2v0 |
(x) |
|
|||||||||
M x (x)= EI p |
|
dx |
|
|
, |
M |
z |
(x)= EI |
z |
. |
|||||||||
|
|
|
dx |
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Прогибы от перерезывающих сил Qy (x), Qz (x) обычно малы по сравнению с прогибами от изгибов v0 (x) и w0 (x) и можно их не учитывать. Осевое перемещение U произвольной точки стержня с координатами x, y, z можно найти, складывая с учётом знака перемещения U от растяжения и двух изгибов
U (x, y, z) = u0 |
(x) − y |
dv0(x) |
− z |
dw0 |
(x) |
. |
|
||||
dx |
dx |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Подобным образом находятся и другие |
||
Н.Л. |
M |
y |
|
|
|
|
|
|
величины |
при сложных деформациях |
|
|
|
|
|
|
|
стержней. |
После чего можно решать |
||||
α |
|
|
|
|
+ |
|
|
||||
|
|
|
|
|
|
|
вопрос об их прочности и жёсткости. |
||||
|
|
β |
|
|
|
|
|
|
|||
|
z |
|
|
|
|
|
|
|
Заметим, что полученные соотно- |
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
шения будут справедливы для стержней |
|||
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
с любой формой поперечного сечения, |
||
|
|
|
|
|
|
|
|
|
если они не подвержены кручению. Если |
||
|
|
Рис. 4.3 |
|
|
|
же присутствует кручение, то они спра- |
|||||
|
|
|
|
|
ведливы только для круглых стержней. |
||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Далее рассмотрим некоторые час- |
|
то встречающиеся на практике частные случаи сложных деформаций. |
|||||||||||
4.2. Косой изгиб
Косым изгибом называется общий случай изгиба, при котором изгиб про-
исходит в плоскостях обеих главных центральных осей поперечного сечения стержня.
При косом изгибе осевую силу N (x) и крутящий момент M x (x) полагают равными нулю. Поэтому в соответствии с общей формулой (4.4) для нормальных напряжений имеем
σx (x, y, z) = − MIzz(x) y − MIyy(x)z .

163
Нейтральная линия (на рис. 4.3 обозначена Н. Л.), на которой σx = 0, в соответ-
ствии с |
(4.8) будет задана уравнением |
|
0 |
= by + cz , |
(4.11) |
представляющим собой уравнение прямой, проходящей через начало координат. Из (4.11) с учетом введенных обозначений получим:
|
z |
= − |
b(x) |
= − |
M z (x)I y |
= |
M z*(x)Iy |
= tg α , |
(4.12) |
|
y |
c(x) |
M y (x)Iz |
M *y (x)Iz |
|||||
|
|
|
|
|
|
||||
где M *y (x) , |
M z*(x) – компоненты вектора момента, определяемые в соответст- |
||||||||
вии с правилами знаков теоретической механики (в соответствии с этими правилами составляющая вектора момента вдоль оси считается положительной, если она совпадает с направлением оси), связанные с M y (x), M z (x) соотношениями M y (x) = −M y (x), M z (x ) = M z (x ). Очевидно, что
M = β z tg ,
M y
где β – угол, определяющий направление вектора изгибающего момента в сечении (рис.4.3). Из выражения (4.12) видно, что при J y ¹ Jz , tga ¹ tgb, т. е. a ¹ b и направления вектора M и нейтральной линии в общем случае не совпадают. При этом нейтральная линия всегда поворачивается от направления вектора момента в сторону оси с меньшим моментом инерции, что можно использовать при проверке решения по физическому смыслу. Можно показать, что вектор перемещений точек оси стержня в сечении всегда направлен перпендикулярно нейтральной линии.
Предположим, что вектор изгибающего момента порождается парой сил, равномерно распределенной вдоль всего стержня (рис. 4.3) и плоскость действия этой пары перпендикулярна вектору момента. Перемещения точек оси стержня происходит в плоскости, перпендикулярной нейтральной линии, т. е. ось балки выпучивается из плоскости действия нагрузки. Поэтому такой изгиб называют косым.
Отметим, что при изменении от сечения к сечению соотношения между M z и M y изменяется и направление вектора перемещений точек оси стержня, в
результате чего изогнутая ось стержня оказывается пространственной кривой. Для более детального знакомства с теорией сложных деформаций стерж-
ней можно обратиться к литературе [1 - 5].
4.2.1. Алгоритм расчета балки на косой изгиб
Для балки постоянного поперечного сечения (рис. 4.4), нагруженной в сечениях А силой P1 под углом α1 к оси у (угол α считается положительным, если он отсчитывается против часовой стрелки от оси у) и в сечении В силой P2
под углом α2, требуется:


165
в котором моменты в горизонтальной и вертикальной плоскостях не равны нулю. При этом угол наклона нейтральной линии α по отношению к оси у необходимо вычислять с помощью формулы (4.12).
6. Определить полное перемещение точки А, лежащей на оси балки, для
чего необходимо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А – |
||
а) с помощью интеграла Мора |
вычислить |
перемещения в точке |
||||||||||||||||||
Vy , Vz соответственно в плоскостях 0xy |
и 0xz; |
|
|
|
|
|
|
|
|
|||||||||||
б) полное перемещение в точке А вычислить по формуле |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
VA = |
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Vy2 + Vz2 |
|
|
|
|
|
|
|
|
||||||
|
|
4.2.2. Пример использования алгоритма |
|
|
|
|
||||||||||||||
Рассмотрим балку с нагрузкой, представленной на рис. 4.5. |
|
|
||||||||||||||||||
|
|
|
|
P2 |
|
|
|
P1 |
|
P2 |
y |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
x |
|
|
z |
|
|
|
P |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||
|
|
C |
l/2 |
|
B |
l/2 |
|
|
A |
|
|
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Рис. 4.5 |
|
|
|
|
|
|
|
|
|||||
Исходные данные приняты следующие: l =2 м, |
|
P = 1 кН, |
P2 =1 кН, |
α2 =30°, |
||||||||||||||||
h / b = 5/3, [σ]=1 МПа, E =2.105 МПа. |
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1. Определяем горизонтальные P1z , |
P2z и |
вертикальные P1y , P2y |
состав- |
|||||||||||||||||
ляющие сил P1 и P2 (угол α1 =–90°): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
P1z = P1 sin(−90°) = −1кН, P2z |
= P2 sin(30°) = 0,5 кН; |
|
|
|
|
|||||||||||||||
P1y = P1 cos(−90°) = 0кН, P2 y = P2 cos(30°) = 0,866кН. |
|
|
||||||||||||||||||
2. Строим эпюры изгибающих моментов в плоскости |
0xy – M z (x) |
и в |
||||||||||||||||||
плоскости 0xz |
– M y (x) (рис. 4.5): |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а) эпюра M z (x) в плоскости 0xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
– определяем реакцию RС и сосредоточенный момент MС от вертикаль- |
||||||||||||||||||||
ных сил в заделке из условий равновесия |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
SmС = - MС + P2yl / 2 = - MС + 0,866×1= 0 ; MС = 0,866 кН×м ; |
|
|
||||||||||||||||||
SmB = - MС - RCl / 2 = -0,866- RC ×1 = 0 ; RС = -0,866 кН ; |
|
|
||||||||||||||||||
– строим |
эпюру |
изгибающих |
моментов |
M z (x) |
в |
плоскости |
0xy |
|||||||||||||
( рис. 5,а); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) эпюра M y (x) в плоскости 0xz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
– определяем реакцию RС и сосредоточенный момент |
MС от горизон- |
|||||||||||||||||||

|
|
166 |
|
|
|
|
|
тальных сил в заделке из условий равновесия: |
|
|
|
|
|
||
SmС = - MС + P2zl / 2 - P1zl = - MС + 0,5×1-1×2 = 0 ; MС = -1,5 кН×м ; |
|||||||
SmB = - MС - RСl / 2 - P1zl / 2 = 1,5- RС ×1-1×1 = 0 ; RС = 0,5 кН ; |
|
||||||
|
y |
|
|
|
|
|
|
|
RC = - 0,866кН |
|
P2y=0,866 кН |
|
|
||
MC=0,866 кН.м. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
x |
|
С |
l/2 |
B |
|
l/2 |
A |
|
|
|
|
|
|
|
||
ЭпюраMz ,кН.м. |
0,866 |
|
|
|
|
a |
|
|
z |
= 0,5 кН |
|
|
|
|
|
|
RC |
P2z= 0,5кН |
|
|
|||
M = -1,5 кН.м |
|
|
|
|
|||
|
|
|
|
|
|
|
|
C |
0 |
|
|
|
|
|
x |
|
|
|
|
|
|
||
|
|
|
P |
|
= 1кН |
|
|
|
|
|
1z |
|
|
|
|
ЭпюраMy ,кН.м |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
б |
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
|
|
|
3,366 |
|
|
|
|
|
|
ЭпюраM прив, кН м |
|
|
|
|
|
|
|
|
|
|
1,66 |
|
в |
||
|
|
|
|
|
|
|
|
|
|
Рис. 4.6 |
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
167 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– строим |
|
|
|
|
эпюру |
изгибающих |
моментов |
M y (x) |
в |
плоскости 0xz |
|||||||||||||||||||||||||||||||||||||||
(рис. 4.5, б). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. Строим эпюру приведенных моментов Mприв (x) в соответствии с фор- |
|||||||||||||||||||||||||||||||||||||||||||||||||
мулой (4.15) для k = h / b = 5 / 3 (рис. 4.5, в). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
4. Подбираем размеры прямоугольного поперечного сечения: |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
а) Mпривmax =3,366 кН.м; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
б) подбирам высоту сечения h согласно неравенству |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
6kMпривmax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 × 5 3 × 3,366 ×103 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
h ³ 3 |
|
|
|
|
= 3 |
= 3 33,66 ×10−1 » 0,323м; |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
[s] |
|
|
|
|
|
|
|
1×106 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
b = |
|
|
h = 0,6 × 0,323 = 0,194м . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Проверим прочность сечения для выбранных размеров |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
M привmax |
|
|
3,366 кН ×м ×6 |
= 998 |
|
кН |
= 0,998МПа |
£ [s] =1МПа , |
||||||||||||||||||||||||||||||||||||
smax = |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0,194×0,3232 м3 |
|
м3 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Wz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
из чего видно, что условие прочности выполняется. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
Вычисляем моменты инерции выбранного сечения: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Jz = bh3 = 0,194 ×(0,323)3 |
= 0,545×10−3м4; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
J y = hb3 |
= 0,323 × (0,194)3 |
|
= 0,197 ×10−3м4. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С (x = 0): |
||||||||
5. Определяем |
положение нейтрального |
|
слоя |
для |
сечения |
||||||||||||||||||||||||||||||||||||||||||||
M z (0) = 0,866 кН.м; |
|
|
|
|
M y (0) = −1,5 кН.м; |
|
|
|
J y |
Jz |
= b2 / h2 = (3 / 5)2 = 0,36; |
||||||||||||||||||||||||||||||||||||||
tga = - |
Mz (x) |
|
|
|
Jy |
= - 0,866 ×0,36 = 0,21; угол наклона нейтральной линии по |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
My (x) Jz |
-1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
отношению к оси y равен α = arctg(0,21) = 11°42 = 11,69°. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
y(z) |
|
|
RC=-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
6. Определяем полное пе- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ремещение точки A , |
|
лежащей |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = |
|
|
|||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
на оси балки, для чего: |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– строим эпюры изгибающих |
|||||||||||
|
|
|
|
С |
|
|
|
|
|
l/2 |
|
|
|
|
|
B |
|
|
|
|
l/2 |
|
|
|
|
|
|
|
|
|
|
|
|
(0) |
(0) |
соответ- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
моментов M z |
, M y |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ственно от единичных внешних |
||||||||
Эпюра M(0)(M(0) |
)м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вертикальной и горизонтальной |
||||||||||||
z |
y |
, 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сил, приложенных в |
|
точке A |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 6) (очевидно, что эпюры |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M z(0) и M y(0) одинаковы); |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– с помощью интеграла Мо- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ра |
вычисляем |
перемещение в |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
168 |
|
|
|
|
|
|
|
||
точке A – VyA в плоскости Oxy : |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
VyA = |
|
|
1 |
|
l |
M z (x)M z(0) (x)dx. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
EJ z |
ò0 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Этот интеграл вычисляем с помощью способа Верещагина: |
|
|
|||||||||||||||||||||||||||||
VyA = |
1 |
|
æ |
1 |
× 0,866 ×103 |
×1× |
5 |
|
ö |
= |
|
|
|
0,866 × 5 ×103 |
|
|
= 0,662 ×10−5м; |
||||||||||||||
|
|
ç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
3 |
|
|
|
× 2 ×1011 × 0,545 ×10−3 |
||||||||||||||||||||||||
|
|
EJ z è |
|
|
|
|
|
|
ø |
6 |
|
|
|
||||||||||||||||||
|
|
C помощью интеграла Мора записываем перемещение в точке A – VzA |
|||||||||||||||||||||||||||||
в плоскости Oxz : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
él / 2 |
|
|
|
|
|
|
l |
|
ù |
|
VzA = |
|
|
|
|
òM y (x)M y(0) (x)dx = |
|
|
|
|
|
|
|
ê |
ò M y (x)M y(0) (x)dx + òM y (x)M y(0) (x)dxú. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
EJ y 0 |
|
|
|
|
|
|
|
|
|
|
EJ y ë |
0 |
|
|
|
|
|
|
l / 2 |
|
û |
||||||||
Этот интеграл аналогично вычисляем с помощью способа Верещагина: |
|||||||||||||||||||||||||||||||
VzA = |
1 |
|
é |
|
æ |
1 |
|
|
|
|
|
5 |
ö æ |
|
|
|
3 |
ö æ 1 |
|
|
2 |
öù |
|||||||||
|
|
|
ê- |
ç |
|
× 0,5 ×103 ×1 × |
|
|
|
|
|
÷ - |
ç1 ×103 ×1 × |
|
÷ - ç |
|
×1 ×103 ×1 × |
|
÷ú = |
||||||||||||
|
|
|
2 |
|
3 |
2 |
|
3 |
|||||||||||||||||||||||
|
|
EJ y ë |
|
è |
|
|
|
|
|
ø è |
|
|
|
ø è 2 |
|
|
øû |
||||||||||||||
|
|
|
|
|
|
|
|
|
= - |
|
|
2,25 ×103 |
|
= -5,71×10 |
−5 м; |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
11 |
× |
0,197 ×10 |
−3 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
×10 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
– вычисляем полное пермещение в точке A по формуле
VA = 
 (VyA )2 + (VzA )2 = (
(VyA )2 + (VzA )2 = (
 (0,662)2 + (5,721)2 ) ×10−5 = 5,75 ×10−5 м.
(0,662)2 + (5,721)2 ) ×10−5 = 5,75 ×10−5 м.
4.3. Внецентренное растяжение и сжатие
При внецентренном растяжении-сжатии (нагрузка – сила P параллельна оси стержня и не проходит через центр тяжести поперечного сечения) в попе-
речном сечении появляются продольная сила |
N = P и изгибающие моменты |
|||||||||||||
My = − My = −PzP, Mz = Mz = −PyP, |
следовательно, |
полное нормальное на- |
||||||||||||
пряжение в соответствии с формулой (4.4) |
представляется в виде |
|
||||||||||||
|
N |
|
M z |
|
M y |
|
æ |
|
yP y |
|
|
ö |
|
|
|
|
|
|
P ç |
|
|
zP z ÷ |
|
||||||
sx ( y, z) = |
|
- |
|
y - |
|
z = |
|
ç1 |
+ |
|
+ |
|
÷ . |
(4.16) |
F |
Iz |
I y |
|
2 |
2 |
|||||||||
|
|
|
|
F è |
|
iz |
|
iy |
ø |
|
||||
При внецентренном растяжении нейтральная линия не проходит через центр тяжести поперечного сечения и определяется уравнением
1+ |
yyP |
+ |
zz P |
= 0 . |
(4.17) |
|
iz2 |
iy2 |
|||||
|
|
|
|
В формулах (4.16), (4.17) yP , zP – координаты точки приложения силы относительно главных центральных осей; iz ,iy – главные радиусы инерции сечения стержня.

169
4.3.1.Алгоритм определения допускаемой растягивающей силы
ипостроения эпюры нормальных напряжений
1.Определить радиусы инерции сечения. Для сложного поперечного сечения: а) разбить поперечное сечение на простые фигуры и вычислить площади Fi , моменты инерции J yi ,Jzi ,J yizi относительно горизонтальных и вертикаль-
ных центральных осей каждой фигуры и площадь всего поперечного сечения
F = åFi ;
i
б) провести горизонтальную и вертикальную оси y , z всего сечения через любую точку и вычислить координаты центров тяжести простых фигур yCi , zCi относительно осей y , z ;
в) определить координаты центра тяжести поперечного сечения:
|
|
n |
|
n |
|
|
|
|
|
|
|
|
åFi yCi |
|
å Fi zCi |
||||||
|
yC = |
i=1 |
; zC = |
i=1 |
|
|
(4.18) |
|||
|
F |
F |
|
|
||||||
|
|
|
|
|
|
, |
|
|
||
и провести центральные оси y, z параллельно осям |
|
|
; |
|||||||
y |
z |
|||||||||
г) вычислить моменты инерции всего сечения относительно осей y , z: |
||||||||||
n |
|
n |
|
|
|
n |
||||
Jy = å |
( Jyi + bi2 Fi ) ; Jz = å( Jzi + ai2 Fi ) ; Jyz |
= å( Jyizi + aibi Fi ) , (4.19) |
||||||||
i=1 |
|
i=1 |
|
|
i=1 |
|||||
где n – число простых фигур, на которое разбито поперечное сечение; ai , bi – расстояние между осями zi и z , yi и y:
|
ai = yCi − yC |
; bi = zCi − zC |
; |
|
|
(4.20) |
|||||||
д) определить положение главных осей: |
|
|
|
|
|
|
|||||||
|
|
|
tg2α0 = |
|
|
2Jyz |
|
; |
|
|
|
|
(4.21) |
|
|
|
|
Jz − Jy |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
е) вычислить главные моменты инерции: |
|
|
|
|
|
||||||||
|
|
1 |
é |
|
|
|
|
|
|
ù |
|
|
|
J1,2 |
= |
|
|
|
|
2 |
2 |
, |
(4.22) |
||||
2 |
êJ y + J z ± |
|
|
(J y - J z ) |
+ 4J yz ú |
||||||||
|
|
ë |
|
|
|
|
|
|
|
û |
|
|
|
ж) определить квадраты радиусов инерции: |
|
|
|||||||||||||
|
|
|
i2 |
= J |
1 |
F , i2 |
= J |
2 |
F . |
|
(4.23) |
||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
||
2. |
Определить координаты точки приложения силы yP , zP (относительно |
||||||||||||||
главных центральных осей). |
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. |
Определить положение нейтральной линии поперечного сечения |
||||||||||||||
|
y |
0 |
= -i2 |
y |
P |
, |
z |
0 |
= -i2 z |
P |
(4.24) |
||||
|
|
|
1 |
|
|
|
|
|
|
2 |
|
||||
4.Найти координаты точки, где напряжение достигает максимального значения ( zmax , ymax ), т. е. точку, наиболее удаленную от нейтральной линии.
5.Определить величину допускаемой растягивающей (сжимающей) силы из условия:
170
[P] = |
|
F[σ] |
|
|
. |
(4.25) |
|
|
ymax yP |
|
|||||
1+ |
zmax zP |
|
|||||
|
+ |
|
|
|
|
||
iz2 |
iy2 |
|
|
|
|||
6. Построить эпюру нормальных напряжений, соответствующих значению допускаемой растягивающей (сжимающей) силы, вдоль линии, перпендикулярной нейтральной линии и проходящей через точку, наиболее удаленную от неё.
Примечание. 1. Если сечение имеет хотя бы одну ось симметрии, то эта ось – главная центральная, а вторая – ей перпендикулярна и проходит через центр тяжести поперечного сечения. 2. Для стандартных профилей необходимые величины выписать из соответствующих ГОСТов (см. приложение 1).
Пример использования алгоритма
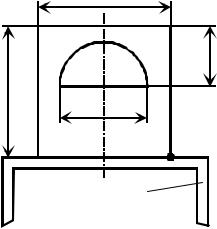
Определить величину допускаемой растягивающей силы P , приложенной в точке поперечного сечения, указанной на рис. 4.8, и построить эпюру нормальных напряжений. Принять [σ] = 100 МПа.
1. Определяем радиусы инерции: а) Поперечное сечение (рис. 4.8) разбиваем на три простые фигуры: швеллер 1, прямоугольник 2, полукруг 3. Попе-
речное сечение – симметричное, |
ось симметрии |
y – главная центральная ось. |
||||||||||||||||||||
Выписываем для швеллера № 8 (ГОСТ 8240 –72) следующие величины: F1 = |
||||||||||||||||||||||
8, 98 см2 ; H = 80 мм; B= 40 мм; y0=1, 31 см; J y 1=89,4 см4; Jz 1=12, 8 см4. |
||||||||||||||||||||||
|
|
|
|
40 |
|
|
|
|
|
Известно, |
что |
для |
швеллера |
|||||||||
|
|
|
|
|
|
|
|
J y 1z1 =0. Для прямоугольника вычисляем: |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2=bh=6.4=24 см2; |
|
|||||
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
Jz2 = bh3 |
= 4×63 |
=72 см4; |
||||||
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= hb3 |
= 6×43 |
|
|||
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
J y2 |
==32 см4; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
P |
|
J y2z2 = 0. |
|
|
12 |
12 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Швеллер |
|
|
|
|
|
Для полукруга вычисляем: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Швеллер № 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
N8 |
|
|
|
|
F3 = |
1 |
|
pD2 |
= 3,14×22 = 1,57см2 ; Jy3z3 = 0 ; |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|||||||||
|
|
|
|
Рис. 4.8 |
|
|
|
2 |
1 pD4 |
8 |
3,14 × 24 |
|
|
|||||||||
|
|
|
|
|
|
|
|
J y3 = |
= |
= 0,393 см4; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
64 |
|
|||||||
|
|
|
|
pD4 |
|
|
|
|
3,14 × 24 |
|
|
|
|
128 |
|
|
||||||
J |
z3 |
= |
1 |
- e2F = |
- (0,212 × 2)2 ×1,57 = 0,110 см4. |
|
||||||||||||||||
|
|
|
||||||||||||||||||||
|
2 |
64 |
3 |
128 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Определяем площадь всего сечения:
F = F1 + F2 − F3 = 8,98 + 24 - 1,57 = 31,41 см2;
б) определяем координаты центров тяжести каждой фигуры:
