Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Расчет стержней и стержневых систем

.pdf

Скачиваний:

806

Добавлен:

12.03.2015

Размер:

3.89 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2016 17 18 19 20 > Следующая >>>

151

одном, наиболее напряженном сечении каждого пролета, напряжения равнялись допускаемому, следует определить соотношения жесткостей, пропорцио-

нальных

моментам

инерции,

вычисленным

из

условий прочности

( J

= J

= 9840 см4 , J

= 2790cм4 ). Если принять k =1, то

EJ1

J1 ×l2

9840×9

= 2,25

;

EJ2

9840× 4

J2 ×l1

EJ1

J1 ×l3

9840×5

= 4,4.

EJ3

9840× 4

J3 ×l1

Эти

соотношения

жесткостей

удовлетворяют условию прочности при

эпюре изгибающих моментов (см. рис. 3.21, в), построенной при k1 = 4/3 =1,33, k2 = 9/5 =1,8, k3 = 5/ 2 = 2,5 . Поэтому необходимо провести расчет при новых соотношениях жесткостей: k1 =1, k2 = 2,25, k3 = 4,4 . Если значения эпюр из-

гибающих моментов и повторного и первоначального расчетов будут мало отличаться друг от друга и при подборе поперечных сечений из условия прочности номер`а двутавров совпадут с номерами двутавров сечений, подсчитанных с учетом приведенных жесткостей ( k1 =1, k2 = 2,25, k3 = 4,4 ), то расчет нераз-

резной балки заканчивается. В противном случае расчет необходимо повторить. Расчет при новых соотношениях жесткостей. Уравнение (3.16) запишем в

виде;

2M 2 (1+ 2,25)+ M3 ×2,25 = -6[26,66 ×1+ 60× 2,25];

M 2 × 2,25 + 2M3(2,25 + 4,4)- 40 × 4,4 = -6[60 × 2,25 +15,625× 4,4]

или

6,5M2 + 2,25M3 = -969,99 ; 2,25M 2 +13,3M3 = -1046,5 .

Решение этих уравнений дает значение лишних неизвестных

M 2 = -129,6 кН ×м ; M3 = -56,8 кН × м.

Опорные реакции при этом получаются равными

R1 = 47,6 кH ; R2 =180,5 кH ; R3 = 80,3 кH ; R4 = 61,6 кH .

Статическая проверка:
			R1 + R2 + R3 + R4 - q1l1 - 2P2 - P3 - q4l4 = 47,6 +
	+180,5 + 80,3 + 61,6 - 40 × 4 - 60× 2 - 50 - 20× 2 = 370 - 370 = 0 .
Кинематическая проверка: при κ1 =1, κ																											2 = 2,25,							κ		3 = 4,4				коэффициенты
ki = li κi		получат							новые			значения:												k2 = 4,					k3 =1,136.										Тогда,			согласно
рис. 3.20, ж, е, перемещение на опоре 3 будет:
		1		é	1		60 ×9 æ 9						ö		1			9			1			1		50 ×5			5		1 æ			1			5		5 ö		1
d3	=			ê		×				ç	+ 9÷ ×						×			×			+		×			×		×			ç		×			+	÷	×		+
d3	=		EJ0	ê	2	×	3			ç	+ 9÷ ×				9		×	2		×	4		+	2	×	4		×	2	×	5		ç	3	×		2	+	÷	×	1,136	+
			EJ0	ë	2		3			è 3			ø		9			2			4			2		4			2		5		è	3			2		2 ø		1,136
					+			1	×	50 ×5	×	5	×	1	×	2		×	5		×		1			- 56,8×9×						1	×	9	×		1	-
					+		2		×	4	×		×		×			×			×	1,136				- 56,8×9×					9		×	2	×		4	-
							2			4	2		5		3			2				1,136									9			2			4

															152
		-		1	(129,6 - 56,8) ×9×								1	×	1		×9×		1	- 40×5×		1	×	5	×		1	-
		-			(129,6 - 56,8) ×9×								9	×	3		×9×		4	- 40×5×			×		×	1,136		-
		2											9		3				4	5			2			1,136
-	1	(56,8 - 40)5×					1	×	2	×5	×		1		ù		=		1		(203,74		- 203,84) =						0,1	.
																ú
	2						5		3							ú													EJ0
	2		0,1×100%				5		3			1,136û						EJ0											EJ0
Погрешность			0,1×100%			= 0,05% .
Погрешность		203,84				= 0,05% .
		203,84
Строим эпюры Qy (x)								и M z (x)						(рис. 3.22, б, в). Из эпюры M z (x) определя-

ем M max = 98,93 кН × м . Из условия прочности определим момент сопротивления

W =W =

max

98,93 ×103

= 0,618 ×10−3(м3 ) = 618 (cм3) ,

[s]

160 ×106

по

сортаменту

определим

W =W = 597(cм3),

двутавр

номер

33,

= 9840 cм4 , p

= J

= p

= 42,2 кг/м .

Проверка по прочности показывает, что

s =

max

98,93×103

=165(МПа) ,

табл

0,597 ×10−3

\перенапряжение 3% (что допустимо);

−3

max × Smax

112,4 ×103 × 0,6339 ×10

= 55 (МПа) <100 (МПа) .

× b

0,984 ×10−4 × 7 ×10−3

W =W = 251cм3 ;

3-м

4-м

пролетах

= 40 кН × м ,

= 2780 cм4 ;

= J

= p

= 25,8 кг/м .

Проверка

по

прочности

дает:

max

40 ×103

= 158,1(МПа) , т.е. недонапряжение 1,18 % ;

10−3

W табл

0,253 ×

max × Smax

51,9 ×103 × 0,141×10−3

= 49,4 (МПа) <100 (МПа) .

× b

0,279 ×10−4 × 5,3×10−3

Масса балки

G = p1(l1 + l2 ) + p3(l3 + l4 ) = 42,2 ×13 + 25,8 × 7 = 72,92 (кгс) .

Неразрезная балка постоянной изгибной жесткости

Имеем k1 = k2 = k3 = k4 =1. Тогда k1 = l1 = 4 ; k2 = l2 = 9 ; k3 = l3 = 5 и урав-

нения (3.16) примут вид:

éS

×l +

(l + l

) + M

×l

= -6ê

ú ;

éS

×l

+ l ) + M

×l = -6ê

ú ;

153
2M 2(4 + 9)+ 9M3 = -6[106,66 + 540];
9M2 + 2M3(9 + 5)- 40 ×5 = -6[540 + 78,125];
26M2 + 9M3 = -3880,0 ; 9M2 + 28M3 = -3508,75.
Из решения уравнений находим M 2 = -119,1кН × м ;	M3 =
= -87, 02 кН × м .

Рис. 3.22

Опорные

реакции

R1 = 50, 22 кH ;

R2 =173, 34 кH ;

R3 = 90, 84 кH ;

R4 = 55, 6 кH .

Статическая проверка:

R1 + R2 + R3 + R4 - q1l1 - 2P2 - P3 - q4l4 = 50,22 +

+173,34 + 90,84 + 55,6 - 40 × 4 - 60 × 2 - 50 - 20 × 2 = 370 - 370 = 0 .

Кинематическая проверка (рис. 3.20, з, е):

P l

é1

P l

æ l

× 2

2 + l

× R

3 3

× R

÷ +

EJ0 ë2 3

2 2 4 2

3 2 2 ø

																									154
+	1	P3l3	×	l3		× R ×		2 ×			l3		- M			×l			× R ×				l2		-			1	(M			- M					)l × R ×				l2	- M				×l × R ×		l3	-
+	1	4	×			× R ×		2 ×					- M			×l			× R ×				2		-			2	(M			- M					)l × R ×					- M				×l × R ×		2	-
	2	4	2				4	3		2				3		1		2		2			2					2			2	2			3			2	2		3				4	3	4	2
													-			1	(M			3	- M				4		)l × R ×					2	×l			ù =
													-				(M				- M						)l × R ×						×l			ù =
															2													3		4		3		3		ú
															2																	3				û
							1	é		1			60×9		æ 9						ö		1			9			1		50 ×5						5		1 æ 1		5		5	ö
					=				ê	2		×	3		ç				+	9÷		×	9	×		2		+	2	×		4			×		2	×	ç	×	2	+	2	÷ +
					=				ê			×			ç				+	9÷		×		×				+		×					×			×	ç	×		+		÷ +
							EJ0 ë								è 3						ø																		5 è 3					ø

+ 12 × 504×5 × 52 × 15 × 23 × 52 - 87,02×9× 19 × 92 -

-12 (119,1- 87,02) ×9 × 19 × 13 ×9 - 40×5× 15 × 52 -

	1		1		2	ù		1	(618,12	- 618,08)=	0,04
-		(87,02 - 40)5×		×		×5ú	=					.
	2		5		3			EJ0			EJ0
						û

Погрешность 0,04×100% = 0,007%. 618,12

Строим эпюры Qy(x) и M z(x) (рис. 3.22, г, д). Из эпюры M z(x) определяем M max = 82,3 кН × м . Подбираем размеры балки двутаврового сечения

Wz =

max

82,3 ×103

= 0,514 ×10−3(м3 ) = 514 (cм3) .

[s]

160 ×106

Wz = 518 см3 ,

По ГОСТу

имеем

двутавр

номер 30а,

для которого

J z = 7780 см4 , p

= 39, 2 кг/м.

Проверка на прочность показывает, что:

smax

max

82,3 ×103

=158,8 (МПа) , недонапряжение 0,69%;

0,518 ×10−3

tmax =

max

× Szотс

109,78×103

× 0,292 ×10−3

= 6,33 (МПа) <100 (МПа).

J z × b

0,778×10−

4 × 6,5 ×10−3

Сравним варианты расчетов неразрезной балки по массе. Масса балки при

произвольно заданном соотношении жесткостей на

954,1- 729, 2

×100% = 30,08%

729,2

больше, а масса балки с постоянной жесткостью на

784 - 729,2

×100% = 7,5%

729,2

больше, чем масса балки с оптимальным соотношением жесткостей ( κ1 = 1, κ2 = 2,25, κ3 = 4,4 ). Таким образом, рациональный подбор соответствующих жесткостей дает значительную экономию в массе.

155

3.7. Задание на выполнение расчетно-графической работы «Расчет неразрезных балок»

Целью задания является расчет в исследование объема неразрезной балки при изменении нагрузки, жесткости и формы поперечного сечения.

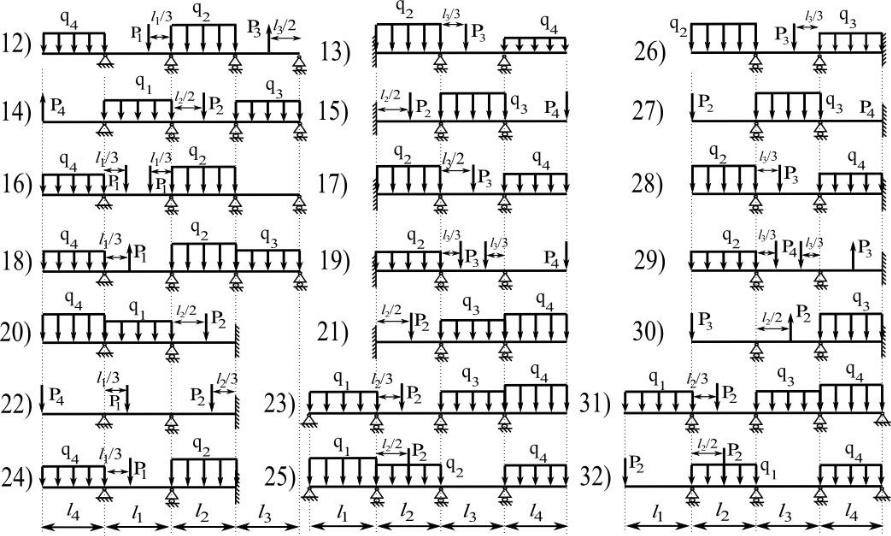
Для заданной схемы (рис. 3.23 или 3.24) требуется:

1) построить эпюры перерезывающих сил в изгибающих моментов, подобрать размеры балки двутаврового и прямоугольного поперечного сечений (при отношении сторон прямоугольника α = hb ) для ступенчато переменного по-

перечного сечения и проверить прочность балки по нормальным и касательным напряжениям для обоих сечений;

2)выполнить второй вариант расчета для балок постоянной жесткости, т.е. при ki = 1;

3)графическая часть задания для двух вариантов расчета должна содержать: схематический чертеж заданной балки (в масштабе) с указанием размеров

инагрузки, схематический чертеж основной системы; эпюры перерезывающих сил и изгибающих моментов.

Примечания.	нагрузки принять: q0 = 10 кН/м;	l0 =1 м; P0 = 10 кН;
1. Основные
M 0 = 2 кН∙м; остальные данные взять из табл. 3.2, воспользовавшись шифром,
который выдал преподаватель, и соотношениями;		qi = q0mi ; Pi = P0mi ;
Mi = M0mi ; li = l0ni ;	Ii = I0ki , где i =1; 2; 3; 4.

2.Материал балки вдоль оси один и тот же (постоянный): [σ] =140 МПа;

[τ]= 80 МПа.

3.Для рис. 3.24 номер схемы выбирается по шифру. Сосредоточенные внешние силы и моменты приложены в серединах указанных пролетов.

																					Таблица 3.2
Номер	m , n		m	2	, n	2	m , n		m	4	, n	4	k	k	2	k	3	, α	k	4		Номер схемы
строки	1	1		2		2	3	3		4		4	1		2		3			4		для рис. 3.24
строки																						для рис. 3.24

	г			в			б				а		б	в				г	а			г

1	10			6			2			1			1	5			2		1			1
2	9			6			3			2			2	4			3		2			2
3	8			7			4			3			3	3			4		3			3
4	7			8			5			4			3	2			5		4			4
5	6			9			5			4			2	1			4		4			5
6	5			10			6			3			1	3			3		3			6
7	4			2			7			2			2	4			2		2			7
8	3			3			8			1			3	2			3		1			8
9	2			4			9			2			4	3			4		2			9
0	4			5			10			3			5	2			2		3			10

156

Рис. 3.23

157

Рис. 3.23 (продолжение)

158

Рис. 3.24

159

4. РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ НА СЛОЖНЫЕ ДЕФОРМАЦИИ

4.1. Расчетные соотношения для стержней при действии нагрузки общего вида

В реальных стержнях под действием произвольной нагрузки возникают одновременно все виды деформаций. Решение в этом общем случае получается по принципу суперпозиции линейных задач, согласно которому следует складывать одноименные величины, найденные для отдельных видов деформаций. Однако для отдельных видов деформации решения были получены в главных центральных осях поперечного сечения, которые далее обозначим x, y, z .

Чтобы решить задачу, необходимо, очевидно, предварительно разложить нагрузку общего вида по указанным осям. После этого следует найти (построить) эпюры внутренних силовых факторов в этих осях. Их будет шесть, по числу составляющих двух векторов (силы и момента) в поперечном сечении Q {Qx*, Q*y , Q*z }, M {M x*, M *y , M *z }. Напомним, что эпюры внутренних силовых

факторов Qx (x)= N(x), Qy (x), Qz (x), M x (x), M y (x), M z (x) строятся для величин, которые совпадают с проекциями векторов с точностью до знака.

Когда найдены эпюры внутренних силовых факторов, можно определить, например, нормальные напряжения в поперечных сечениях. Эти напряжения вызываются тремя из шести силовыми факторами N(x), M y (x), M z (x)

σx 1

σx 2

σx 3

= N(x) , F

=− MIzz(x) y ,

=− M y (x)z . I y

(4.1)

(4.2)

(4.3)

При одновременном действии всех трёх внутренних силовых факторов N(x), M y (x), M z (x) возникающие в поперечных сечениях нормальные напря-

жения представляют собой по принципу суперпозиции сумму напряжений от

каждого из силовых факторов

σx = σx 1 + σx 2

+ σx 3

N(x)

−

M z (x)

y −

M y (x)

z ,

(4.4)

I z

I y

откуда видно, что в общем случае напряжение σx представляет собой функцию всех трёх координат x, y, z :

σx = σx (x, y, z) .

(4.5)

Зависимость этого напряжения от продольной координаты x определяется зависимостями от этой координаты эпюр внутренних силовых факторов. В направлении же поперечных координат зависимости линейные. Если зафиксиро-

160

вать координату x, т.е. рассмотреть одно из поперечных сечений, то коэффици-

енты в соотношении (4.4) будут постоянными. Обозначим их
a =	N(x)	, b = −	M z (x)	, c = −	M y (x)	.	(4.6)
	F		Iz		I y

Нормальное напряжение в выбранном поперечном сечении будет функцией только от двух координат y и z, а поскольку эти зависимости линейны, поверхность, изображающая нормальное напряжение, окажется плоскостью, что видно и из получающейся формулы для напряжений

σx = σx (y, z)= a + by + cz .	(4.7)
Плоскость поперечного сечения и плоскость напряжений σx (y, z)	могут

пересекаться (рис. 4.1). Пересечение плоскостей происходит по прямой линии. Уравнение этой прямой получается, если положить нормальное напряжение в

сечении равным нулю σx = 0 :
		a + by + cz = 0 .				(4.8)
	σx (y, z)< 0		нейтральная		Напомним, что прямая, на которой
	y		линия		отсутствуют	нормальные напряжения в
	y		линия		отсутствуют	нормальные напряжения в
					поперечном	сечении, называется ней-
z 0					поперечном	сечении, называется ней-
z 0					тральной линией. В зависимости от па-
					тральной линией. В зависимости от па-
					раметров задачи нейтральная линия мо-
					жет пересекать контур сечения, как это
					изображено на рис. 4.1, так и проходить
			σx (y, z)> 0	x	вне сечения. Нейтральная линия (н.л.)
			σx (y, z)> 0	x	отделяет, очевидно, растянутую часть се-
			Рис. 4.1		чения, где σx > 0 , от сжатой его части,

где σx < 0 . Если нейтральная линия проходит вне контура сечения, то всё сече-

ние оказывается под действием напряжений одного знака.

В рассматривавшихся теориях сдвига и кручения стержней предполагалось, что от перерезывающих сил Qy (x), Qz (x) и крутящего момента M x (x)

нормальных напряжений не возникает.

Помимо нормальных напряжений в поперечных сечениях стержней могут действовать касательные напряжения. Последние возникают под действием как раз перерезывающих сил и крутящего момента. Касательные напряжения от перерезывающих сил могут быть грубо оценены как средние по сечению

τxy сд = −

Qy (x)

, τxz сд = −

(x)

(4.9)

или тоже приближённо, но более точно по формуле Журавского

τxy сд = −

Qy (x)Sz (y)

τxz сд

= −

Qz (x)S y (z)

(4.10)

Izb(y)

I y b(z)

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2016 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.03.20151.18 Mб45расч_УМ_2013 Изменён Вставка 10_10_13.doc
#
12.03.2015642.73 Кб48Расчёт гидравлической системы.docx
#
01.05.2025380.51 Кб0Расчёт защит заземл Методичка.docx
#
12.03.2015431.1 Кб220Расчёт несущей перемычки 3 ПБ16.doc
#
12.03.20151.23 Mб71Расчет режимов резания.doc
#
12.03.20153.89 Mб806Расчет стержней и стержневых систем.pdf
#
18.12.2018958.98 Кб9РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО.DOC
#
12.03.20153.26 Mб106Расчет_РРЛ_2.pdf
#
12.03.201520 Mб20Расчетно-графическая работа по ИВТ.doc
#
16.11.2018413.18 Кб8Расчетно-графическая работа № 1_Осень.doc
#
12.03.2015599.19 Кб135Расчетное задание по экологии для заочников.docx