Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Расчет стержней и стержневых систем

.pdf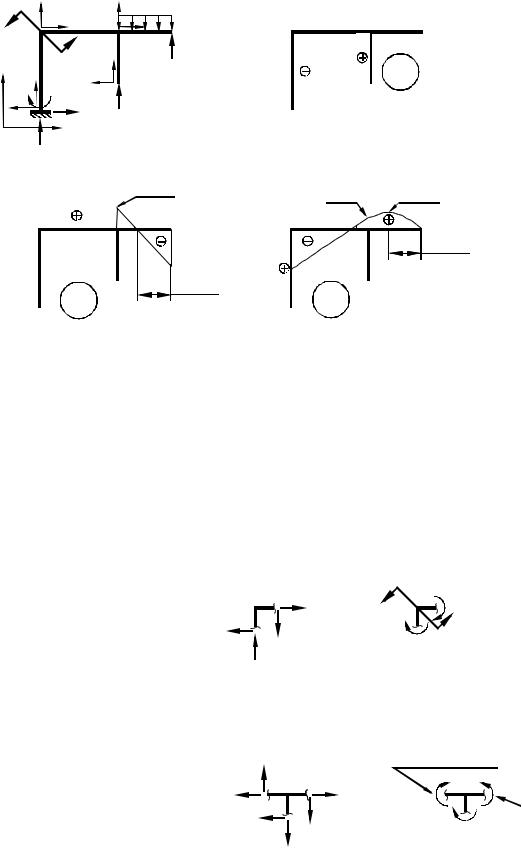

Скачиваний:

806

Добавлен:

12.03.2015

Размер:

3.89 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2013 14 15 16 17 18 19 20 > Следующая >>>

121

X2=24,94 кН

3,63

X1=-3,63 кН

кН

18,69

15,06

9,88

15,55

-24,94

13,81

1,25 м

-46,19

1,25 м

кН

13,81 кН.м

Рис. 3.8 8. Проверяем правильность построенных итоговых эпюр внутренних

силовых факторов.

Статическая проверка (проверка равновесия узлов).

Вырежем из рамы узлы B и C, заменив действие отброшенных частей внутренними усилиями и моментами. Проверим для каждого узла выполнение уравнений равновесия.

Узел B (рис. 3.9):

å x = 0; − Qy3 + N4 = −0 + 0 ≡ 0.	B N4=0	M=60 кН.м	M4=46,19 кН.м
å y = 0; − N3 − Qy4 =	B N4=0	B
å y = 0; − N3 − Qy4 =	Qy3=0
= −(−18,69) +18,69 = 0.	Qy4=18,69 кН	M3=13,81кН.м
åmB = 0; M − M3 − M4 =	N3=18,69 кН
åmB = 0; M − M3 − M4 =
= 60−13,81− 46,19 = 0.	Рис. 3.9

Узел C (рис. 3.10):

å x = 0; − N3 − Qy2 + N1 =	Qy3=18,69 кН			M3=9,88 кН.м
å x = 0; − N3 − Qy2 + N1 =		C		C
= −0 − 0 + 0 ≡ 0.	N3=0	C	N1=0	C
= −0 − 0 + 0 ≡ 0.	N3=0		N1=0
å y = 0; Qy3 − N2 − Qy1 =	Qy2=0		Q =15,06 кН	M =0
= 18,69 − 3,63−15,06 = 0.			y1	2

	åmC = 0; − M3 − M2 + M1 =	N2=3,63 кН
		Рис. 3.10
	−9,88− 0+ 9,88 = 0.

м . Н к

8 8 , 9 = 1 M

122

Таким образом, уравнения равновесия узлов удовлетворяются. Заметим, что на рис. 3.9 и 3.10 изображены положительные направле-

ния внутренних усилий N и Qy . Величины этих усилий с учетом знака снимаются с соответствующих эпюр. Изгибающие моменты на этих рисунках показаны с учетом их фактического направления, определяемого по эпюре Mz . Напомним, что эпюра изгибающих моментов располагается со стороны сжатых волокон.

Деформационная проверка.
Выбираем новую основную систему, отбра-	B		C	D
сывая две связи в опоре A (рис 3.11). Строим		O
эпюры изгибающих моментов в новой основной		O	E
эпюры изгибающих моментов в новой основной			E
системе от единичных обобщенных усилий, при-	A

ложенных в направлении отброшенных связей:

Рис. 3.11

От момента X3 = 1 (рис. 3.12, а).

Определяем из уравнений равновесия опорные реакции.

åx = HA = 0; Þ HA = 0.

åmD = - X3 + HAl - RE l1 = 0; Þ RE = -0,5 м−1.

åmC = - X3 + HAl + RDl1 = 0; Þ RD = 0,5 м−1.

Проверка: å y = 0; RE + RD = -0,5+ 0,5 = 0.

Записываем по участкам аналитические выражения для изгибающих моментов, вычисляем их значения в характерных точках и строим эпюру Mz3.

Участок DC (0 ≤ x1 ≤ l1 = 2 м): Mz3 (x1) = RD x1 = 0,5x1;

Mz3 (x1 = 0) = 0; Mz3 (x1 = l1) = 1.

Участок EC

(0 ≤ x2 ≤ l1 = 2 м): Mz3 (x2 ) = 0.

Участок AB

(0 ≤ x3 ≤ l = 3 м):

Mz3 (x3 ) = X3 − HA x3 = 1.

Участок BC

(0 ≤ x4 ≤ l = 3 м):

Mz3 (x4 ) = X3 − HAl = 1.

xC2

y x3

X3=1

Mz3 кН.м

x HA

Эпюра Mz3 показана на

Рис. 3.12

рис. 3.12, б.

От усилия X4 = 1 (рис. 3.13, а).

Определяем из уравнений равновесия опорные реакции.

123

åx = HA = 0; Þ HA = 0.

åmD = - X4 (l + l1) + HAl - RE l1 = 0; Þ RE = -2,5.

åmC = - X4l + HAl + RDl1 = 0; Þ RD = 1,5.

Проверка:

å y = 0;

X4 + RE + RD = 1+1,5- 2,5 = 0.

Записываем по участкам аналитические выражения для изгибающих

моментов, вычисляем их зна-

чения в характерных точках и

строим эпюру Mz4 .

Участок DC

(0 ≤ x1 ≤ l1 = 2 м):

Mz4

Mz4 (x1) = RD x1 = 1,5x1;

x HA

M z4 (x1 = 0) = 0;

M z4 (x1 = l) = 3 м .

X4=1

Рис. 3.13

Участок EC (0 ≤ x2 ≤ l1 = 2 м):

Mz4 (x2 ) = 0.

Участок AB (0 ≤ x3 ≤ l = 3 м):

Mz4 (x3) = −HA x3 = 0.

Участок BC (0 ≤ x4 ≤ l = 3 м):

Mz4 (x4 ) = X4 x4 − HAl = x4.

Mz4 (x4 = 0) = 0; Mz4 (x4 = l) = 3 м.

Эпюра Mz4

показана на рис. 3.13, б.

Определяем по формуле Мора перемещения в направлении связей, от-

брошенных в узле A. Эти перемещения должны равняться нулю.

ò M zi M z dx

(i = 3,4) .

EJ z

k =1 0

él1

dx +

ú =

EJ z

êò

4 ú

ë0

é2

0,5x (24,94x -10x

2 )dx +

1×13,81dx +

1×

(-46,19 +18,69x

)dx

ú =

EJ z

êò

4 ú

=EJ1 z (24,94 x13 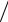6 −10 x14 8) 20 +13,81x3 30 + (−46,19x4 +18,69x42 2) 30 =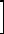

=(158,79 −158,57) EJz = 0,22 EJz ≈ 0.

Погрешность равна 158,570,22 100%≈ 0,14%< 5%.

124

él1

dx +

ú =

EJ z ê

4 ú

é2

1,5x (24,94x -10x 2 )dx +

(-46,19 +18,69x

)dx

EJ z

êò

=EJ1 z (37,41x13 3−15x14 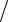4) 20 + (−46,19 x42 2 +18,69x43 3) 30 =.

=(267,97 − 267,86) EJz = 0,11 EJz ≈ 0 м.

Погрешность равна 267,860,11 100%≈ 0,04%< 5%.

Таким образом, погрешность деформационной проверки не превышает допустимой.

По результатам статической и деформационной проверок делаем вывод, что эпюры внутренних силовых факторов построены верно.

9. Подбираем параметры поперечных сечений.

Из анализа эпюр (рис. 3.8) определяем максимальные величины внутренних силовых факторов.

Участок

AB:

max =13,81 кН×м,

max = 18,69 кН .

Участок

BC:

max = 46,19 кН×м в сечении B; N = 0.

Qy max = 24,94 кН в сечении D.

Из условия прочности по максимальным нормальным напряжениям от изгиба определяем требуемый момент сопротивления поперечного сечения.

Wт ³

max

46,19×103

= 288,68×10−6

м3 = 288,68 см3.

160×106

Из таблицы ГОСТ 8239-56 (см. приложение) выбираем двутавр №24 с

параметрами:

= 289 см3,

F = 34,8 см2,

S отс

=163 см2,

= 3460 см4

z max

s = 5,6 мм.

Проверим прочность подобранного сечения по нормальным напряжениям.

На участке AB:

smax =

max

18,69×103

13,81×103

= (5,37 + 47,79)×106

34,8×10−4

289×10−6

= 56,16 МПа <

На участке BC заведомо

smax <

так как здесь N = 0, а W > Wт .

125

Проверим прочность по касательным напряжениям.

max

Szотсmax

24,94×103 ×163×10−6

= 20,95 МПа <

tmax =

Jz s

3460×10−8 ×5,6×10−3

Таким образом, двутавр №24 удовлетворяет условиям прочности. Момент сопротивления квадратного сечения записывается с помощью

формулы для прямоугольного сечения

Wz = b63 .

Используя требуемый момент сопротивления данной задачи, найдем соответствующий ему размер стороны квадратного сечения

b ³ 36 × 288,89 =12,0123см .

Примем h =12см. Проверим прочность стержня, нагруженного максимальным

моментом, для этого размера поперечного сечения

max

N (x)

M z (x)

max

= 0 +

6 × 46,19 кН × м

=160, 38 МПа

>160МПа.

123 см3

Перегруз сечения (погрешность) δ составляет меньше допустимых 3 % :

d =

max - [s]

×100 % =

160, 38 -160

×100 % = 0,238 % < 3 % .

[s]

160

Проверим прочность сечений на стержне AB, которые также могут быть

нагружены опасными напряжениями:

max

M z

max

18,69 кН

6 ×13,81кН × м

= (1,30 + 47,95) МПа =

12 ×12 см2

123см3

= 49,25 МПа < [σ] ,

так что нормальные напряжения во всей раме для прочности не опасны. Проверяем прочность по касательным напряжениям:

max

=1,5

сред

Qy (x)

max

=1,5

24,94 кН

= 2,60 МПа < [t] .

144 см2

Все условия прочности для квадратного сечения 12×12см выполняются, такое сечение тоже можно использовать.

126

3.4.Пример расчета статически неопределимой рамы методом сил

спомощью системы компьютерной алгебры Maxima

Запускаем wxMaxima и вводим первый оператор

В первой строке виден оператор kill(all); который он делает недоступными результаты предыдущей работы – уничтожает все переменные. Это сделано для удобства возможных перевычислений, в случае исправления ошибки. Вводим требуемые величины: интенсивность распределенной нагрузки, длины участков, момент. В качестве символа присваивания используется : . В качестве разделителя выражений используется ;

Выбираем основную систему. Сначала определяем реакции (см. рис. 3.5), для этого запишем уравнения статики:

Определяем настройки для решения систем уравнений:

Решая систему уравнений, находим реакции:

127

Проверяем найденные реакции, вычисляя суммарный момент в точке D:

Определяем функции – выражения изгибающих моментов по участкам (рис. 3.5). Первый участок:

Второй участок:

Третий участок:

Четвертый участок:

По этим выражениям строится эпюра изгибающих моментов от внешних сил. Прикладываем к основной системе единичную обобщенную силу X1 (рис. 3.6):

Ищем реакции (рис. 3.6), для чего записываем уравнения равновесия:

128

Решая систему уравнений, находим реакции:

Проверяем найденные реакции, для чего записываем сумму моментов в точке С:

Рассматриваем каждый участок рамы и записываем для них выражения изгибающих моментов.

Первый участок:

Второй участок:

Третий участок:

Четвертый участок:

Теперь прикладываем к основной системе единичную обобщенную силу

X 2 (рис. 3.7):

129

Ищем реакции (рис.3.7), для этого записываем уравнения равновесия:

Решая систему уравнений, находим реакции:

Проверяем найденные реакции, для этого записываем сумму моментов в точке С:

Рассматриваем каждый участок рамы и записываем для них выражения изгибающих моментов. Первый участок:

Второй участок:

Третий участок:

130

Четвертый участок:

После того как были получены все выражения для изгибающих моментов, можно искать коэффициенты системы канонических уравнений. Коэффициент

EJ z δ11 :

<пропущен промежуточный вывод Maxima>

Коэффициент EJ zδ22 :

<пропущен промежуточный вывод Maxima>

Коэффициент EJ zδ12 :

<пропущен промежуточный вывод Maxima>

Коэффициент EJ z 1 :

<пропущен промежуточный вывод Maxima>

Коэффициент EJ z 2 :

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2013 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.03.20151.18 Mб45расч_УМ_2013 Изменён Вставка 10_10_13.doc
#
12.03.2015642.73 Кб48Расчёт гидравлической системы.docx
#
01.05.2025380.51 Кб0Расчёт защит заземл Методичка.docx
#
12.03.2015431.1 Кб218Расчёт несущей перемычки 3 ПБ16.doc
#
12.03.20151.23 Mб71Расчет режимов резания.doc
#
12.03.20153.89 Mб806Расчет стержней и стержневых систем.pdf
#
18.12.2018958.98 Кб9РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО.DOC
#
12.03.20153.26 Mб105Расчет_РРЛ_2.pdf
#
12.03.201520 Mб20Расчетно-графическая работа по ИВТ.doc
#
16.11.2018413.18 Кб8Расчетно-графическая работа № 1_Осень.doc
#
12.03.2015599.19 Кб135Расчетное задание по экологии для заочников.docx