
- •Федеральное агентство по образованию
- •1.Цель и задачи дисциплины, её место в учебном процессе.
- •Задачи изучения дисциплины. Требования к знаниям и умениям студента.
- •2. Содержание и структура дисциплины.
- •Раздел III. Аналитическая геометрия
- •Тема 5. Прямые линии и плоскости.
- •Тема 6. Кривые и поверхности второго порядка
- •Дополнительная литература:
- •4. Методические указания по изучению дисциплины.
- •5. Материалы для контроля знаний студентов.
- •3.1. 3.2.
- •Раздел II. Векторная алгебра.
- •Раздел III. Аналитическая геометрия.
- •Раздел IV. Введение в анализ.
- •Раздел V. Комплексные числа. Алгебра многочленов.
- •6. Приложения.
- •6.1. Образец решения контрольных задач типового варианта.
- •, .
- •6.2. Краткие теоретические сведения.
- •Тема 1. Определители.
- •Тема 2. Матрицы.
- •Тема 3. Системы линейных уравнений.
- •Тема 4. Векторная алгебра.
- •3) ; 4)
- •3) ; 4)5);
- •1) ; 2);
- •Тема 5. Прямые линии и плоскости.
- •Тема 6. Кривые второго порядка.
- •Тема 7. Множества. Числовые множества. Функция.
- •Тема 8. Предел функции. Эквивалентные функции.
- •Тема 9. Непрерывность функции.
- •Тема 10. Комплексные числа и многочлены.
- •6.3 Образец оформления обложки с контрольной работой.
6. Приложения.
6.1. Образец решения контрольных задач типового варианта.
1.1 – 30. Вычислить определитель:


а) непосредственным разложением по
 строке;
строке;б) непосредственным разложением по
 столбцу;
столбцу;Решение. а) вычисляем определитель разложением по элементам первой строки:

 =
= .
.





Тогда
 =
= =
=
б) вычисляем определитель непосредственным разложением по элементам второго столбца:

 =
=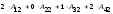 .
.





Тогда
 =
= =
= .
.Ответ:

 .
.2.1-30. а) Найти матрицу
 ,если:
,если:, .
Решение:
1) Транспонируем матрицу
 :
: .
.2) Вычисляем произведение матриц
 :
:

 .
.3) Находим матрицу
 :
:

 .
.4) Находим матрицу
 :
: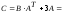

 .
.Ответ:
 .
.3.1 – 30. Дана система уравнений:
 .Требуется:
.Требуется:
а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса.
Решение.
А) Метод Крамера.
1а) Вычисляем определитель системы и проверяем, что он отличен от нуля:

 .
.2а) Так как
 ,
то система имеет единственное решение,
определяемое формулами Крамера:
,
то система имеет единственное решение,
определяемое формулами Крамера:
3а) Вычисляем определители
 :
:
 ,
,
 ,
,
 .
.4а) Находим решение:
 .
.5а) Выполняем проверку:

 .
.Ответ:
 .
.Б) Метод обратной матрицы.
1б) Записываем систему уравнений в матричном виде:
 или
или

2б) Вычисляем определитель системы и проверяем, что он отличен от нуля:


3б) Так как
 ,
то матрица системы
,
то матрица системы имеет обратную матрицу
имеет обратную матрицу и единственное решение системы
определяется формулой:
и единственное решение системы
определяется формулой:
 или
или

4б) Находим обратную матрицу
 (методом присоединённой матрицы):
(методом присоединённой матрицы): .
.








Тогда
 .
.5б) Находим решение:

 .
.6б) Выполняем проверку:

 .
.Ответ:
 .
.В) Метод Гаусса.
1в) Записываем расширенную матрицу системы:
 .
.2в) Выполняем прямой ход метода Гаусса.
В результате прямого хода матрица системы
 должна быть преобразована с помощью
элементарных преобразований строк к
матрице
должна быть преобразована с помощью
элементарных преобразований строк к
матрице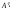 треугольного или трапециевидного вида
с элементами
треугольного или трапециевидного вида
с элементами .
Система уравнений, матрица которой
.
Система уравнений, матрица которой является треугольной с элементами
является треугольной с элементами
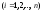 ,
имеет единственное решение, а система
уравнений, матрица которой
,
имеет единственное решение, а система
уравнений, матрица которой является трапециевидной с элементами
является трапециевидной с элементами
 ,
имеет бесконечно много решений.
,
имеет бесконечно много решений.







 .
В результате
элементарных преобразований матрица
.
В результате
элементарных преобразований матрица
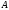 системы преобразована к специальному
виду
системы преобразована к специальному
виду .
Система уравнений, матрица которой
.
Система уравнений, матрица которой ,
является треугольной с ненулевыми
диагональными элементами
,
является треугольной с ненулевыми
диагональными элементами ,
имеет всегда единственное решение,
которое находим, выполняя обратный
ход.
,
имеет всегда единственное решение,
которое находим, выполняя обратный
ход.Замечание. Если при выполнение преобразования расширенной матрицы
 в преобразованной матрице
в преобразованной матрице появляется строка
появляется строка ,
где
,
где ,
то это говорит о несовместности исходной
системы уравнений.
,
то это говорит о несовместности исходной
системы уравнений.3в) Выполняем обратный ход метода Гаусса.
Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода:
 и последовательно из уравнений системы,
начиная с последнего, находим значения
всех неизвестных:
и последовательно из уравнений системы,
начиная с последнего, находим значения
всех неизвестных: .
.4в) Выполняем проверку:

 .
.Ответ:
 .
.4.1-30. Найти общее решение для каждой из данных систем методом Гаусса:
а)
 .
.Решение.
1а) Записываем расширенную матрицу системы:
 .
.2а) Выполняем прямой ход метода Гаусса.

















 .
.Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных
 и
и :
: .
Поэтому выбираем в качестве базисных
– неизвестные
.
Поэтому выбираем в качестве базисных
– неизвестные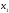 и
и ,
тогда свободными будут неизвестные
,
тогда свободными будут неизвестные и
и .
.3а) Выполняем обратный ход метода Гаусса.
Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода:
 .
Свободным неизвестным придаём разные,
произвольные постоянные значения:
.
Свободным неизвестным придаём разные,
произвольные постоянные значения: ,
, ,
и последовательно из уравнений системы,
начиная с последнего, находим значения
всех базисных неизвестных:
,
и последовательно из уравнений системы,
начиная с последнего, находим значения
всех базисных неизвестных: .
.Тогда общее решение системы запишется в виде:
 .
.4а) Выполняем проверку:

 .
.Ответ:
 .
.б)
 .
.Решение.
1а) Записываем расширенную матрицу системы:
 .
.2а) Выполняем прямой ход метода Гаусса.

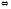






Замечание. В результате прямого хода матрица системы
 должна быть преобразована с помощью
элементарных преобразований строк к
матрице
должна быть преобразована с помощью
элементарных преобразований строк к
матрице треугольного или трапециевидного вида
с элементами
треугольного или трапециевидного вида
с элементами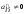 .
.Если, при выполнении преобразования расширенной матрицы
 ,
в преобразованной матрице
,
в преобразованной матрице появляется строка
появляется строка ,
где
,
где ,
то это говорит о несовместности исходной
системы уравнений.
,
то это говорит о несовместности исходной
системы уравнений.Для выполнения условия
 может
потребоваться перестановка местами
столбцов матрицы системы.
Если при
выполнении преобразований прямого
хода в матрице системы переставлялись
местами столбцы коэффициентов при
неизвестных, то в дальнейшем, при записи
системы уравнений, соответствующей
последней расширенной матрице прямого
хода, это следует учесть.
может
потребоваться перестановка местами
столбцов матрицы системы.
Если при
выполнении преобразований прямого
хода в матрице системы переставлялись
местами столбцы коэффициентов при
неизвестных, то в дальнейшем, при записи
системы уравнений, соответствующей
последней расширенной матрице прямого
хода, это следует учесть.














 .
.Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы, с учётом перестановки местами столбцов, образуют первый и второй столбцы коэффициентов при неизвестных
 и
и :
: .
Поэтому выбираем в качестве базисных
– неизвестные
.
Поэтому выбираем в качестве базисных
– неизвестные и
и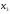 ,
тогда свободными будут неизвестные
,
тогда свободными будут неизвестные и
и .
.3б) Выполняем обратный ход метода Гаусса.
Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода:
 .
Свободным неизвестным придаём разные,
произвольные постоянные значения:
.
Свободным неизвестным придаём разные,
произвольные постоянные значения: ,
, ,
и последовательно из уравнений системы,
начиная с последнего, находим значения
всех базисных неизвестных:
,
и последовательно из уравнений системы,
начиная с последнего, находим значения
всех базисных неизвестных: .
.Тогда общее решение системы запишется в виде:

4б) Выполняем проверку:



Ответ:
 .
.в)
 .
.Решение.
1в) Записываем расширенную матрицу системы:
 .
.2в) Выполняем прямой ход метода Гаусса.










 .
.При выполнении преобразования расширенной матрицы
 ,
в преобразованной матрице
,
в преобразованной матрице появилась строка
появилась строка ,
соответствующая уравнению
,
соответствующая уравнению ,
которому не удовлетворяет ни один набор
значений неизвестных
,
которому не удовлетворяет ни один набор
значений неизвестных ,
что говорит о несовместности исходной
системы уравнений.
,
что говорит о несовместности исходной
системы уравнений.Ответ: Система несовместна.
5.1– 30. Даны векторы
 :
: ;
; ;
; ;
; .
Требуется:а)
вычислить
скалярное произведение векторов
.
Требуется:а)
вычислить
скалярное произведение векторов
 ,
если
,
если
 ,
, ;
б)вычислить
векторное произведение векторов
;
б)вычислить
векторное произведение векторов
 ;в)
показать,
что векторы
;в)
показать,
что векторы
 образуют базис
образуют базис и найти координаты вектора
и найти координаты вектора в
этом базисе.
в
этом базисе.Решение.
1a). Находим вектор


=

 .
.2а)Находим вектор


=

 .
.3а) Вычисляем скалярное произведение векторов
 :
: .
.б) Вычисляем векторное произведение векторов
 :
:
=

1в) Покажем, что векторы
 образуют
базис
образуют
базис
 .Для этого
составим определитель, столбцами
которого являются координаты этих
векторов и покажем, что он отличен от
нуля.
.Для этого
составим определитель, столбцами
которого являются координаты этих
векторов и покажем, что он отличен от
нуля. .
.Так как
 ,
то векторы
,
то векторы образуют
базис
образуют
базис
 и, следовательно,
вектор
и, следовательно,
вектор
 единственным образом можно разложить
по векторам этого базиса.
единственным образом можно разложить
по векторам этого базиса.2в) Записываем разложение вектора
 по векторам базиса
по векторам базиса :
: или
или
 .
.Коэффициенты разложения
 ,
, ,
, называют координатами вектора
называют координатами вектора в базисе
в базисе
 и записывают:
и записывают:
 .
.3в) Записываем векторное уравнение относительно
 ,
, ,
, в виде эквивалентной ему системы
линейных уравнений:
в виде эквивалентной ему системы
линейных уравнений: ,
и находим единственное решение системы,
например, по формулам Крамера:
,
и находим единственное решение системы,
например, по формулам Крамера: ,
где
,
где  ,
, ,
, ,
, .
.Таким образом:
 ,
, ,
, .
Следовательно, разложение имеет вид:
.
Следовательно, разложение имеет вид: или кратко:
или кратко: .
.Ответ:
 .
.6.1-30. Даны вершины треугольника
 :
: ,
, ,
, Требуется найти:
Требуется найти:а) длину стороны
 ;
б)уравнение
стороны
;
б)уравнение
стороны
 ;
;в) уравнение медианы
 ,
проведённой из вершины
,
проведённой из вершины
 ;
;г) уравнение высоты
 ,
проведённой из вершины
,
проведённой из вершины
 ;
;д) длину
 высоты
высоты
 ;
е)площадь
;
е)площадь
 треугольника
треугольника
 .Сделать
чертёж.
.Сделать
чертёж.Решение. Сделаем чертёж:

а) Длину стороны
 находим как
длину вектора
находим как
длину вектора
 :
: ,
, .
.б)Уравнение стороны
 находим как уравнение прямой, проходящей
через точки
находим как уравнение прямой, проходящей
через точки и
и ,
и записываем его в виде общего уравнения
прямой:
,
и записываем его в виде общего уравнения
прямой:






 .
.в) Уравнение медианы
 находим как уравнение прямой, проходящей
через точки
находим как уравнение прямой, проходящей
через точки и
и ,
и записываем его в виде общего уравнения
прямой. Неизвестные координаты точки
,
и записываем его в виде общего уравнения
прямой. Неизвестные координаты точки находим как координаты точки, делящей
сторону
находим как координаты точки, делящей
сторону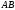 пополам:
пополам: ;
;
 .
.Тогда:







 .
.г) Уравнение высоты
 находим как уравнение прямой, проходящей
через точку
находим как уравнение прямой, проходящей
через точку перпендикулярно вектору
перпендикулярно вектору ,
который принимаем за нормальный вектор
прямой
,
который принимаем за нормальный вектор
прямой .
Тогда
.
Тогда



д) Длину
 высоты
высоты находим как расстояние от точки
находим как расстояние от точки до прямой
до прямой ,
заданной общим уравнением
,
заданной общим уравнением :
: .
.е) Площадь треугольника
 находим по
формуле:
находим по
формуле:
 .
Откуда
.
Откуда .
.Ответ: а)
 ;
б)
;
б)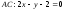 ;
в)
;
в) ;
;г)
 ;
д)
;
д) ;
е)
;
е) .
.7.1 – 30. Даны вершины пирамиды
 .Требуется
найти:
.Требуется
найти: а) длины ребер
 и
и ;
б)угол
между ребрами
;
б)угол
между ребрами
 и
и ;
;в) площадь грани
 ;
г)объем
пирамиды
;
г)объем
пирамиды
 ;
;д) уравнение плоскости грани
 ;
;е) длину
 высоты
высоты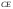 пирамиды
пирамиды
 .
.Решение.
а) Длины рёбер
 и
и
 находим как
длины векторов
находим как
длины векторов
 и
и :
: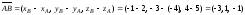 ;
;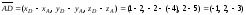 ;
; ;
; .
.б)Угол
 между рёбрами
между рёбрами и
и
 находим как
угол между векторами
находим как
угол между векторами
 и
и по формуле:
по формуле: .
Учитывая, что:
.
Учитывая, что: ,
, ,
, получим
получим .
Откуда
.
Откуда
в) Площадь
 грани
грани находим,
используя геометрический смысл
векторного произведения векторов, по
формуле
находим,
используя геометрический смысл
векторного произведения векторов, по
формуле
 .
Учитывая, что:
.
Учитывая, что:
 ,
,
 ,получим
,получим
 .
.г) Объём
 пирамиды
пирамиды находим,
используя геометрический смысл
смешанного произведения векторов, по
формуле
находим,
используя геометрический смысл
смешанного произведения векторов, по
формуле
 .
Учитывая, что:
.
Учитывая, что: ,
, ,
,получим
 .
.д) Уравнение плоскости грани
 находим как уравнение плоскости,
проходящей через точки
находим как уравнение плоскости,
проходящей через точки ,
, и
и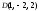 ,
и записываем его в виде общего уравнения
плоскости:
,
и записываем его в виде общего уравнения
плоскости:






е) Длину
 высоты
высоты пирамиды
пирамиды
 находим как расстояние от точки
находим как расстояние от точки
 до плоскости
до плоскости ,
заданной общим уравнением
,
заданной общим уравнением :
: .
.Ответ: а)
 ,
, ;
б)
;
б)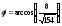 ;
в)
;
в) ;
;г)
 ;
д)
;
д) ;
е)
;
е) .
.8.1–30. Установить, какую кривую определяет алгебраическое уравнение второго порядка, построить её:
а)
 ;
б)
;
б)
 ;
;
в)
 .
.Решение:
а) Выделяя полные квадраты в левой части уравнения
 ,
преобразуем
его следующим образом:
,
преобразуем
его следующим образом:




 .
.Полученное уравнение определяет гиперболу с центром в точке
 и осями симметрии параллельными
координатным осям. Для построения
гиперболы в системе координат
и осями симметрии параллельными
координатным осям. Для построения
гиперболы в системе координат :1)
отмечаем центр гиперболы
:1)
отмечаем центр гиперболы
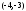 ;2)
проводим через центр
;2)
проводим через центр
 пунктиром оси симметрии гиперболы;3)
строим пунктиром основной прямоугольник
гиперболы с центром
пунктиром оси симметрии гиперболы;3)
строим пунктиром основной прямоугольник
гиперболы с центром
 и сторонами
и сторонами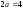 и
и параллельными осям симметрии;4)
проводим
через противоположные вершины основного
прямоугольника пунктиром прямые,
являющиеся асимптотами гиперболы, к
которым неограниченно близко при
бесконечном удалении от начала координат
приближаются ветви гиперболы, не
пересекая их; 5)
изображаем сплошной линией ветви
гиперболы (рис. 1).
параллельными осям симметрии;4)
проводим
через противоположные вершины основного
прямоугольника пунктиром прямые,
являющиеся асимптотами гиперболы, к
которым неограниченно близко при
бесконечном удалении от начала координат
приближаются ветви гиперболы, не
пересекая их; 5)
изображаем сплошной линией ветви
гиперболы (рис. 1).Ответ: Гипербола с центром в точке
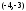 (см.
рис.1)..
(см.
рис.1)..
Рис.1
б) Выделяя полные квадраты в левой части
уравнения
 ,
преобразуем
его следующим образом:
,
преобразуем
его следующим образом:





 .
.Полученное уравнение определяет эллипс с центром в точке
 и осями симметрии параллельными осям
координат. Для построения эллипса в
системе координат
и осями симметрии параллельными осям
координат. Для построения эллипса в
системе координат :1)
отмечаем центр эллипса
:1)
отмечаем центр эллипса
 ;2)
проводим через центр
;2)
проводим через центр
 пунктиром оси симметрии эллипса;3)
строим пунктиром основной прямоугольник
эллипса с центром
пунктиром оси симметрии эллипса;3)
строим пунктиром основной прямоугольник
эллипса с центром
 и сторонами
и сторонами и
и параллельными осям симметрии;4)
изображаем сплошной линией эллипс,
вписывая его в основной прямоугольник
так, чтобы эллипс касался его сторон в
точках пересечения прямоугольника с
осями симметрии (рис.2).
параллельными осям симметрии;4)
изображаем сплошной линией эллипс,
вписывая его в основной прямоугольник
так, чтобы эллипс касался его сторон в
точках пересечения прямоугольника с
осями симметрии (рис.2).Ответ: Эллипс с центром в точке
 (см. рис.2).
(см. рис.2).в). Выделяя полные квадраты в левой части уравнения
 ,
преобразуем
его следующим образом:
,
преобразуем
его следующим образом: 

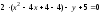



Полученное уравнение определяет параболу с вершиной в точке
 и осью симметрии параллельной оси
и осью симметрии параллельной оси .
Для построения параболы в системе
координат
.
Для построения параболы в системе
координат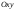 :1)
отмечаем вершину параболы
:1)
отмечаем вершину параболы
 ;2)
проводим через вершину
;2)
проводим через вершину
 пунктиром ось симметрии параболы;3)
изображаем сплошной линией параболу,
направляя её ветвь, с учётом того, что
параметр параболы
пунктиром ось симметрии параболы;3)
изображаем сплошной линией параболу,
направляя её ветвь, с учётом того, что
параметр параболы
 ,
в положительную сторону оси
,
в положительную сторону оси (рис.3).
(рис.3).Ответ: Парабола с вершиной в точке
 (см. рис.3).
(см. рис.3).
Рис.2. Рис.3.
9.1-30. Требуется:
а) найти область определения функции
 ;
;
б) установить чётность (нечётность) функции
 .
.Решение. а) Естественную область определения находим как множество
 всех значений аргумента
всех значений аргумента функции, для которых формула
функции, для которых формула имеет смысл:
имеет смысл: .
Решив (на числовой прямой) систему
неравенств
.
Решив (на числовой прямой) систему
неравенств ,
устанавливаем, что геометрическим
образом множества
,
устанавливаем, что геометрическим
образом множества является промежуток
является промежуток .
.б) Находим сначала естественную область определения функции
 :
:
 .
Решив (на числовой прямой) неравенство
.
Решив (на числовой прямой) неравенство
 ,
устанавливаем, что геометрическим
образом множества
,
устанавливаем, что геометрическим
образом множества является объединение промежутков
является объединение промежутков .
.Так как область
 является симметричной относительно
точки
является симметричной относительно
точки ,
то проверяем выполнение для всех
,
то проверяем выполнение для всех условий:
условий: или
или ,
учитывая чётность и нечётность основных
элементарных функций, входящих в
аналитическое выражение
,
учитывая чётность и нечётность основных
элементарных функций, входящих в
аналитическое выражение .
.Если область
 не симметрична относительно точки
не симметрична относительно точки ,
то
,
то на этом множестве является функцией
общего вида.
на этом множестве является функцией
общего вида.Для этого находим
 .
Поскольку
.
Поскольку для всех
для всех

 ,
то функция
,
то функция является чётной.
является чётной.
Ответ: а)

 ,
, ;
;б) функция
 - чётная.
- чётная.10.1-30. Вычислить пределы (не пользуясь правилом Лопиталя):
а)
 б)
б) в)
в) г)
г) д)
д)
Вычисление предела
 ,
где
,
где ,
начинают всегда с подстановки в
,
начинают всегда с подстановки в предельного значения её аргумента
предельного значения её аргумента .
В результате могут получиться
неопределённости
.
В результате могут получиться
неопределённости ,
, ,
, ,
которые раскрывают тождественными
преобразованиями
,
которые раскрывают тождественными
преобразованиями такими, чтобы преобразованное выражение
получилось определённым. При вычислении
пределов используют свойства конечных
пределов и бесконечно больших функций,
а также следующие известные пределы:
такими, чтобы преобразованное выражение
получилось определённым. При вычислении
пределов используют свойства конечных
пределов и бесконечно больших функций,
а также следующие известные пределы:
 ,
, ,
,
 (
(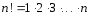 ),
), ,
, ,
, ,
, ,
, .
.Решение. а)
 При подстановке
вместо переменной
При подстановке
вместо переменной
 её предельного значения
её предельного значения получим неопределённость
получим неопределённость .
Для её раскрытия сначала разделим
числитель и знаменатель дроби на
.
Для её раскрытия сначала разделим
числитель и знаменатель дроби на (старшую степень переменной
(старшую степень переменной в числителе и знаменателе), после чего
используем свойства конечных пределов
и бесконечно больших функций. Получим
в числителе и знаменателе), после чего
используем свойства конечных пределов
и бесконечно больших функций. Получим


 .
.б)
 При подстановке вместо переменной
При подстановке вместо переменной
 её предельного значения
её предельного значения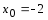 получим неопределённость
получим неопределённость .
Для её раскрытия выделим в числителе
и знаменателе дроби общий множитель
вида
.
Для её раскрытия выделим в числителе
и знаменателе дроби общий множитель
вида ,
где
,
где - некоторое число, т.е. множитель
- некоторое число, т.е. множитель .
Затем сократим на него числитель и
знаменатель дроби, после чего используем
свойства пределов.
.
Затем сократим на него числитель и
знаменатель дроби, после чего используем
свойства пределов.1) В квадратном трёхчлене
 множитель выделяют разложением
квадратного трёхчлена по формуле
множитель выделяют разложением
квадратного трёхчлена по формуле ,
где
,
где .2)
В выражении
.2)
В выражении
 множитель выделяют следующим способом:
множитель выделяют следующим способом:

 .
.В результате получим




 .
.в)
 При подстановке вместо переменной
При подстановке вместо переменной
 её предельного значения
её предельного значения получим неопределённость
получим неопределённость .
Выделим в числителе множители вида
.
Выделим в числителе множители вида ,
где
,
где при
при и используем свойства пределов. Получим
и используем свойства пределов. Получим


Для раскрытия неопределённостей
 ,
содержащих тригонометрические и
обратные тригонометрические функции,
в числителе и знаменателе дроби выделяют
сначала множители вида:
,
содержащих тригонометрические и
обратные тригонометрические функции,
в числителе и знаменателе дроби выделяют
сначала множители вида: ,
, ,
, ,
, ,
где
,
где при
при ,
используя формулы тригонометрии:
,
используя формулы тригонометрии: ,
,
 ,
, .После чего
применяют свойства пределов, учитывая,
что:
.После чего
применяют свойства пределов, учитывая,
что:
 ,
,
 ,
, ,
, .
.

 .
.г)

Для раскрытия неопределённости
 ,
возникающей при вычислении предела
,
возникающей при вычислении предела ,
где
,
где ,
, ,
сначала выражение
,
сначала выражение
 представляют в виде
представляют в виде
 ,
где
,
где при
при .
После чего используют свойства пределов,
заменяя выражение
.
После чего используют свойства пределов,
заменяя выражение его предельным значением
его предельным значением и учитывая, что
и учитывая, что =
= .
.При подстановке вместо переменной
 её предельного значения
её предельного значения получим неопределённость
получим неопределённость .
Представим
.
Представим в виде
в виде ,
где
,
где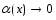 при
при
 ,следующим
способом:
,следующим
способом:

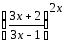 =
= .
Тогда учитывая, что
.
Тогда учитывая, что ,
,
 ,
получим
,
получим =
=
 =
= .
.Ответ: а)
 ;
б)
;
б)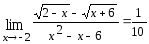 ;в)
;в) ;
г)
;
г) .
.11.1-30. Для указанной функции
 требуется:
а) выяснить
при каких значениях параметра
требуется:
а) выяснить
при каких значениях параметра
 функция
будет
непрерывной;
б) найти
точки разрыва
функции и исследовать их характер.
Построить
график функции.
функция
будет
непрерывной;
б) найти
точки разрыва
функции и исследовать их характер.
Построить
график функции.
а)
 ;
б)
;
б) .
.Решение.
Точками разрыва функции
 являются точки разрыва функций
являются точки разрыва функций в промежутках
в промежутках ,
, ,…,
,…, ,
кроме того, точками возможного разрыва
функции
,
кроме того, точками возможного разрыва
функции являются точки
являются точки в окрестности которых и в самих точках
функция задаётся разными аналитическими
выражениями.
в окрестности которых и в самих точках
функция задаётся разными аналитическими
выражениями.Точка
 является точкой непрерывности функции
является точкой непрерывности функции тогда и только тогда, когда:
тогда и только тогда, когда: .
.а) Поскольку функции
 и
и непрерывны в промежутках
непрерывны в промежутках и
и как элементарные функции, определённые
в каждой точке данных промежутков, то
непрерывность
функции
как элементарные функции, определённые
в каждой точке данных промежутков, то
непрерывность
функции
 может
нарушиться только в точке её возможного
разрыва
может
нарушиться только в точке её возможного
разрыва
 .
.Определяем значение параметра
 из условия непрерывности функции
из условия непрерывности функции в точке
в точке :
: .
Вычисляя
.
Вычисляя
 ,
, ,
, :
: ,
, ,
, ,
из условия непрерывности
,
из условия непрерывности ,
находим
,
находим .
.График непрерывной функции
 имеет вид изображённый на рис. 1.
имеет вид изображённый на рис. 1.б) Функции
 и
и непрерывны в промежутках
непрерывны в промежутках и
и как элементарные функции, определённые
в каждой точке данных промежутков, а
функция
как элементарные функции, определённые
в каждой точке данных промежутков, а
функция в промежутке
в промежутке имеет точкой разрыва точку
имеет точкой разрыва точку ,
в которой она не определена. Тогда для
функции
,
в которой она не определена. Тогда для
функции точка
точка является точкой разрыва, а точки
является точкой разрыва, а точки и
и ,
в окрестности которых и в самих точках
функция задаётся разными аналитическими
выражениями, являются точками возможного
разрыва.
,
в окрестности которых и в самих точках
функция задаётся разными аналитическими
выражениями, являются точками возможного
разрыва.Исследуем на непрерывность точки
 :
:1)




 .
.Следовательно, точка
 - точка разрыва 1-го рода функции
- точка разрыва 1-го рода функции .
.2)

 Следовательно,
точка
Следовательно,
точка
 - точка бесконечного разрыва (2-го рода)
функции
- точка бесконечного разрыва (2-го рода)
функции .
.3)




 .
.Следовательно, точка
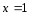 - точка непрерывности функции
- точка непрерывности функции .
.График функции
 имеет вид, изображённый на рис.2.
имеет вид, изображённый на рис.2.Ответ: а) Функция
 непрерывна при
непрерывна при (рис.1);б)
(рис.1);б)
 - точка разрыва 1-го рода,
- точка разрыва 1-го рода,
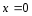 -точка
бесконечного разрыва функции
-точка
бесконечного разрыва функции
 (рис.2).
(рис.2).


Рис.1 Рис.2
12.1-30. Даны комплексные числа
 ,
, ,
, и алгебраическое уравнение
и алгебраическое уравнение .
Требуется:а)
вычислить
.
Требуется:а)
вычислить ,
,
 ,
, ;
б)представить
комплексное число
;
б)представить
комплексное число
 в тригонометрической форме, вычислить
в тригонометрической форме, вычислить и результат представить в алгебраической
форме;в)
найти все
корни алгебраического уравнения на
множестве комплексных чисел.
и результат представить в алгебраической
форме;в)
найти все
корни алгебраического уравнения на
множестве комплексных чисел. Решение.
1а) Вычисляем
 :
:
 .
.
2а) Вычисляем
 .
.Сначала находим


 (учитываем,
что
(учитываем,
что )
) .
Тогда
.
Тогда

3а) Вычисляем
 :
:

 (учитываем,
что
(учитываем,
что
 )
) .
.1б) Представляем комплексное число
 в
тригонометрической форме
в
тригонометрической форме
 ,
где
,
где
 (так
как комплексное число, изображается
точкой
(так
как комплексное число, изображается
точкой
 ,
лежащей в третьем квадранте координатной
плоскости). Тогда
,
лежащей в третьем квадранте координатной
плоскости). Тогда .
.2б) Вычисляем
 по формуле Муавра:
по формуле Муавра:




 .
Полученный результат представляем в
алгебраической форме:
.
Полученный результат представляем в
алгебраической форме:
 .
.1в) Для нахождения корней алгебраического уравнения
 ,
раскладываем его левую часть на
множители:
,
раскладываем его левую часть на
множители: .
.2в) Находим корни уравнения на множестве комплексных чисел, приравнивая каждый из множителей нулю (число корней, с учётом кратности, должно равняться порядку уравнения):
1)


 .
.2)


 .
.3)
 .
Так как дискриминант квадратного
уравнения
.
Так как дискриминант квадратного
уравнения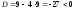 ,
то уравнение имеет два комплексно-сопряжённых
корня:
,
то уравнение имеет два комплексно-сопряжённых
корня: .
.Замечание. Корни
 ,
, можно найти и как корни уравнения
можно найти и как корни уравнения ,
по формуле
,
по формуле .
Для нахождения комплексных значений
корня, число
.
Для нахождения комплексных значений
корня, число следует представить в виде комплексного
числа в тригонометрической форме:
следует представить в виде комплексного
числа в тригонометрической форме: ,
после чего значения корня найти по
формуле:
,
после чего значения корня найти по
формуле: ,где
,где
Ответ: a)
 ,
,
 ,
,
 ;
;б)
 ;
в)
;
в)
 ,
, ,
, .
.6.2. Краткие теоретические сведения.
Тема 1. Определители.
Квадратной матрицей порядка
 называется квадратная таблица из чисел
называется квадратная таблица из чисел
 (
(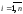 ,
, ):
): ,
состоящая из
,
состоящая из строк и
строк и столбцов. У квадратной матрицы различают
главную диагональ:
столбцов. У квадратной матрицы различают
главную диагональ: и побочную диагональ:
и побочную диагональ: .
Любой квадратной матрице
.
Любой квадратной матрице порядка
порядка можно поставить в соответствие число
можно поставить в соответствие число ,
равное алгебраической сумме
,
равное алгебраической сумме слагаемых, составленных определённым
образом из элементов
слагаемых, составленных определённым
образом из элементов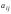 матрицы
матрицы ,
называемое определителем матрицы.
Кратко обозначается
,
называемое определителем матрицы.
Кратко обозначается
 ,
, .
.Определителем 1-ого порядка называется число
 .
.Определителем 2-ого порядка называется число
 .
.Определителем 3-его порядка называется число

 .
.Минором элемента
 называется определитель
называется определитель ,
полученный из определителя
,
полученный из определителя вычёркиванием
вычёркиванием -ой
строки и
-ой
строки и -ого
столбца.
-ого
столбца.Алгебраическим дополнением
 элемента
элемента
 называется его минор
называется его минор
 ,
взятый со знаком
,
взятый со знаком :
: .
.Определителем порядка
 называется число
называется число 
Разложением определителя
 по
по -ой
строке
(
-ой
строке
( )
называется соотношение:
)
называется соотношение: .
.Разложением определителя
 по
по -ому
столбцу
(
-ому
столбцу
( )
называется соотношение:
)
называется соотношение:
Определители обладают следующими свойствами:
1) определитель не изменится при замене всех его строк столбцами с теми же номерами;
2) определитель изменит знак на противоположный, если переставить местами любые две строки (два столбца) определителя;
3) общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя;
4) определитель равен нулю, если он содержит нулевую строку (столбец), две одинаковые или пропорциональные строки (столбца);
5) определитель не изменится, если к какой-либо строке (столбцу) прибавить другую строку (столбец), умноженную на любое число;
6) определитель треугольного вида (когда все элементы, лежащие по одну сторону одной из его диагоналей равны нулю) равен произведению диагональных элементов:
 .
.
Тема 2. Матрицы.
Матрицей размера
 называется
прямоугольная таблица из чисел
называется
прямоугольная таблица из чисел
 (
( ,
,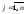 ):
): ,
состоящая из
,
состоящая из строк и
строк и столбцов. Если необходимо указать
размеры матрицы, то пишут
столбцов. Если необходимо указать
размеры матрицы, то пишут .
.Если
 ,
то матрица
,
то матрица называетсяквадратной.
называетсяквадратной.Нулевой называется матрица
 ,
все элементы которой равны нулю,
например:
,
все элементы которой равны нулю,
например: .Единичной
называется квадратная матрица
.Единичной
называется квадратная матрица
 ,
на главной диагонали которой стоят
единицы, а все остальные элементы равны
нулю, например:
,
на главной диагонали которой стоят
единицы, а все остальные элементы равны
нулю, например: .Треугольной
называется квадратная матрица
.Треугольной
называется квадратная матрица
 ,
все элементы которой расположенные по
одну сторону от главной диагонали равны
нулю, например:
,
все элементы которой расположенные по
одну сторону от главной диагонали равны
нулю, например: .Трапециевидной
(ступенчатой)
называется матрица
.Трапециевидной
(ступенчатой)
называется матрица

 ,
все элементы которой, расположенные
ниже элементов
,
все элементы которой, расположенные
ниже элементов
 равны нулю, например:
равны нулю, например: .
.Матрицы
 и
и называютсяравными
и пишут
называютсяравными
и пишут
 ,
если они одинакового размера и их
соответствующие элементы равны:
,
если они одинакового размера и их
соответствующие элементы равны: ,
, ,
, .
.Матрицы можно транспонировать, складывать, вычитать, умножать на число, умножать на другую матрицу.
Транспонированной к матрице
 называется матрица
называется матрица ,
столбцами которой являются соответствующие
строки матрицы
,
столбцами которой являются соответствующие
строки матрицы .
.Суммой (разностью) матриц
 и
и одного размера
одного размера ,
называется матрица
,
называется матрица того же размера, для которой:
того же размера, для которой: ,
,
 ,
, .
.Произведением матрицы
 размера
размера
 на число
на число
 называется матрица
называется матрица
 того же размера, для которой:
того же размера, для которой: ,
, ,
,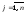 .
.Линейной комбинацией матриц
 и
и
 одного размера
одного размера
 ,
называется матрица
,
называется матрица того же размера (
того же размера ( и
и - произвольные числа), для которой:
- произвольные числа), для которой: ,
, ,
, ,
,Произведением матрицы
 на матрицу
на матрицу называется матрица
называется матрица
 ,
каждый элемент которой
,
каждый элемент которой вычисляется по правилу:
вычисляется по правилу: ,
,
 ,
, .
.Операция умножения матрицы на матрицу определена не для всех матриц, а только для таких у которых число столбцов левой матрицы
 равно числу строк правой матрицы
равно числу строк правой матрицы .
Такие матрицы называются согласованными
для умножения.
Поэтому прежде чем выполнять операцию
умножения матрицы на матрицу следует
проверить их согласованность для
умножения и определить размерность
матрицы-произведения (если умножение
матриц возможно):
.
Такие матрицы называются согласованными
для умножения.
Поэтому прежде чем выполнять операцию
умножения матрицы на матрицу следует
проверить их согласованность для
умножения и определить размерность
матрицы-произведения (если умножение
матриц возможно):
 .
Особенность операции умножения матриц
состоит в том, что в общем случае:
.
Особенность операции умножения матриц
состоит в том, что в общем случае: ,
т.е. переместительное свойство места
не имеет.
,
т.е. переместительное свойство места
не имеет.Элементарными преобразованиями матрицы называются:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число, отличное от нуля;
3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;
4) вычёркивание нулевой строки (столбца).
Матрицы
 и
и ,
полученные одна из другой в результате
элементарных преобразований называютсяэквивалентными
и пишут
,
полученные одна из другой в результате
элементарных преобразований называютсяэквивалентными
и пишут
 .
.Обратной к квадратной матрице
 порядка
порядка ,
называется матрица
,
называется матрица того же порядка, если:
того же порядка, если: ,
где
,
где -
единичная матрица порядка
-
единичная матрица порядка .
.Квадратная матрица
 называетсяневырожденной,
если её определитель
называетсяневырожденной,
если её определитель
 .
Обратная матрица всегда существует
для невырожденных матриц.
.
Обратная матрица всегда существует
для невырожденных матриц.Основными методами вычисления обратной матрицы являются:
Метод присоединённой матрицы. Если
 -невырожденная
матрица, то
-невырожденная
матрица, то ,
где
,
где - присоединённая матрица, для которой:
- присоединённая матрица, для которой:
 .
Здесь
.
Здесь - алгебраические дополнения элементов
- алгебраические дополнения элементов матрицы
матрицы .
.В частности, если
 ,
то
,
то
Метод элементарных преобразований. Для данной квадратной матрицы
 порядка
порядка строится прямоугольная матрица
строится прямоугольная матрица размера
размера приписыванием к
приписыванием к справа единичной матрицы. Далее, с
помощью элементарных преобразований
над строками, матрица
справа единичной матрицы. Далее, с
помощью элементарных преобразований
над строками, матрица приводится к виду
приводится к виду ,
что всегда возможно, если
,
что всегда возможно, если - невырожденная.
- невырожденная.Матричными называются уравнения вида:
 ,
, ,
, ,
,где матрицы
 - известны, матрица
- известны, матрица -
неизвестна. Если квадратные матрицы
-
неизвестна. Если квадратные матрицы и
и - невырожденные, то решения матричных
уравнений записываются, соответственно,
в виде:
- невырожденные, то решения матричных
уравнений записываются, соответственно,
в виде: ,
, ,
, .
.Минором
 -ого
порядка матрицы
-ого
порядка матрицы
 размера
размера
 называется определитель
называется определитель
 квадратной матрицы порядка
квадратной матрицы порядка ,
образованной элементами матрицы
,
образованной элементами матрицы ,
стоящими на пересечении произвольно
выбранных её
,
стоящими на пересечении произвольно
выбранных её строк и
строк и столбцов
столбцов .
.Максимальный порядок
 отличных от нуля миноров матрицы
отличных от нуля миноров матрицы ,
называется еёрангом
и обозначается
,
называется еёрангом
и обозначается
 или
или ,
а любой минор порядка
,
а любой минор порядка ,
отличный от нуля –базисным
минором.
,
отличный от нуля –базисным
минором.
Тема 3. Системы линейных уравнений.
…Система уравнений вида:
 называетсясистемой
называетсясистемой
 линейных уравнений с
линейных уравнений с неизвестными.
Числа
неизвестными.
Числа
 называются коэффициентами системы,
называются коэффициентами системы, - свободными членами системы,
- свободными членами системы, - неизвестными системы.
- неизвестными системы.В матричной форме система имеет вид:
 ,
где
,
где ,
, ,
, .Здесь
.Здесь -матрица
системы,
-матрица
системы, -матрица-столбец
неизвестных,
-матрица-столбец
неизвестных, -матрица-столбец
свободных членов.
-матрица-столбец
свободных членов.Если
 ,
то система называетсяоднородной,
в противном
случае неоднородной.
,
то система называетсяоднородной,
в противном
случае неоднородной.
Система, матрица
 которой является треугольной с
диагональными элементами
которой является треугольной с
диагональными элементами ,
называетсятреугольной.
Система,
матрица
,
называетсятреугольной.
Система,
матрица
 которой является трапециевидной,
называетсятрапециевидной.
которой является трапециевидной,
называетсятрапециевидной.
Решением системы называется всякий упорядоченный набор чисел
 ,
обращающий каждое уравнение системы
в равенство. Совокупность всех решений
называетсямножеством
решений системы.
,
обращающий каждое уравнение системы
в равенство. Совокупность всех решений
называетсямножеством
решений системы.Система называется совместной, если она имеет, по крайней мере, одно решение; определённой, если она имеет только одно решение; неопределённой, если она имеет бесконечно много решений; несовместной, если она не имеет решений.
Однородная система уравнений всегда совместна, так как всегда имеет, по крайней мере, нулевое решение
 .
Треугольная система является определённой,
трапециевидная система – неопределённой.
.
Треугольная система является определённой,
трапециевидная система – неопределённой.Две системы называются эквивалентными, если множества их решений совпадают.
Элементарными преобразованиями систем уравнений называются:
1) перестановка уравнений;
2) перестановка местами слагаемых
 в каждом из уравнений системы;
в каждом из уравнений системы;3) умножение уравнения на число, отличное от нуля;
4) прибавление к уравнению другого, умноженного на любое число;
5) вычёркивание уравнения вида:
 .
.Основными точными методами решения систем линейных уравнений являются методы: Крамера, обратной матрицы и Гаусса.
Если число уравнений в системе
 совпадает с числом неизвестных
совпадает с числом неизвестных и определитель матрицы системы
и определитель матрицы системы ,
то система имеет единственное решение,
которое можно найти:
,
то система имеет единственное решение,
которое можно найти:а) методом Крамера по формулам:
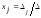 ,
, ,где
,где
 -
определитель, получаемый из определителя
матрицы системы
-
определитель, получаемый из определителя
матрицы системы заменой
заменой -ого
столбца на столбец свободных членов;
-ого
столбца на столбец свободных членов;б) методом обратной матрицы по формуле
 .
.Методом Гаусса находят решение произвольной системы линейных уравнений. Метод состоит в приведении системы уравнений, с помощью элементарных преобразований, к системе специального вида, эквивалентной исходной, решение которой очевидно. Преобразования по методу Гаусса выполняют в два этапа. Первый этап называют прямым ходом, второй - обратным.
В результате прямого хода выясняют: совместна или нет система и если совместна то, сколько имеет решений - одно или бесконечно много, а также, в случае бесконечного множества решений, указывают базисные и свободные неизвестные для записи общего решения системы. Преобразования прямого хода выполняют, как правило, над расширенной матрицей системы
 ,
которую получают, приписывая справа к
матрице системы
,
которую получают, приписывая справа к
матрице системы столбец свободных членов
столбец свободных членов .
В результате элементарных преобразований
строк и перестановкой столбцов, матрица
системы
.
В результате элементарных преобразований
строк и перестановкой столбцов, матрица
системы должна быть приведена к матрице
должна быть приведена к матрице треугольного или трапециевидного вида
с элементами
треугольного или трапециевидного вида
с элементами .
При этом, система уравнений, матрица
которой
.
При этом, система уравнений, матрица
которой ,
является треугольной с диагональными
элементами
,
является треугольной с диагональными
элементами
 ,
будет иметь единственное решение;
система уравнений, матрица которой
,
будет иметь единственное решение;
система уравнений, матрица которой
 ,
является трапециевидной с элементами
,
является трапециевидной с элементами
 ,
будет иметь бесконечно много решений.
Если, при выполнении преобразований
расширенной матрицы
,
будет иметь бесконечно много решений.
Если, при выполнении преобразований
расширенной матрицы ,
в преобразованной матрице
,
в преобразованной матрице появится строка
появится строка ,
где
,
где ,
то это говорит о несовместности исходной
системы уравнений. Базисные неизвестные
указывают, выписывая базисный минор
преобразованной матрицы системы
,
то это говорит о несовместности исходной
системы уравнений. Базисные неизвестные
указывают, выписывая базисный минор
преобразованной матрицы системы .
Базисными являются неизвестные
преобразованной системы, столбцы
коэффициентов
.
Базисными являются неизвестные
преобразованной системы, столбцы
коэффициентов при которых образуют базисный минор
(определитель максимального порядка,
отличный от нуля). Свободными являются
неизвестные, не являющиеся базисными.
при которых образуют базисный минор
(определитель максимального порядка,
отличный от нуля). Свободными являются
неизвестные, не являющиеся базисными.В результате обратного хода находят решение системы, записывая его в виде общего решения, если их бесконечно много. Преобразования обратного хода часто выполняют, над уравнениями системы, соответствующей последней расширенной матрице
 прямого хода. В случае единственного
решения, его получают, находя
последовательно значения всех неизвестных
из уравнений системы, начиная с
последнего. В случае, когда решений
бесконечно много, их записывают в виде
общего решения. Для этого свободным
неизвестным придают разные произвольные
постоянные значения:
прямого хода. В случае единственного
решения, его получают, находя
последовательно значения всех неизвестных
из уравнений системы, начиная с
последнего. В случае, когда решений
бесконечно много, их записывают в виде
общего решения. Для этого свободным
неизвестным придают разные произвольные
постоянные значения: ,
, ,…,
,…, ,
и последовательно из уравнений системы,
начиная с последнего, находят значения
всех базисных неизвестных. Полученное
решение называют общим. Придавая
произвольным постоянным, конкретные
значения, находят частные решения
системы уравнений.
,
и последовательно из уравнений системы,
начиная с последнего, находят значения
всех базисных неизвестных. Полученное
решение называют общим. Придавая
произвольным постоянным, конкретные
значения, находят частные решения
системы уравнений.Тема 4. Векторная алгебра.
Вектором (геометрическим) называется направленный отрезок, задаваемый упорядоченной парой точек (началом и концом вектора). Обозначают вектор
 или
или .
Расстояние между началом и концом
вектора называется егодлиной
и обозначается
.
Расстояние между началом и концом
вектора называется егодлиной
и обозначается
 или
или .Углом между
векторами
.Углом между
векторами
 и
и называется угол
называется угол ,
, ,
на который следует повернуть один из
векторов, чтобы его направление совпало
с направлением другого вектора, при
условии, что их начала совпадают.Проекцией
вектора
,
на который следует повернуть один из
векторов, чтобы его направление совпало
с направлением другого вектора, при
условии, что их начала совпадают.Проекцией
вектора
 на вектор
на вектор называется число
называется число
 .
.Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Векторы называются компланарными, если они расположены в одной плоскости или в параллельных плоскостях.
Векторы
 и
и называютсяравными
и пишут
называютсяравными
и пишут
 ,
если они коллинеарны, одинаково
направлены и имеют равные длины. Векторы
,
если они коллинеарны, одинаково
направлены и имеют равные длины. Векторы и
и называютсяпротивоположными
и пишут
называютсяпротивоположными
и пишут
 ,
если они коллинеарны, направлены в
разные стороны и имеют равные длины.
,
если они коллинеарны, направлены в
разные стороны и имеют равные длины.Суммой векторов
 и
и называется вектор
называется вектор ,
соединяющий начало вектора
,
соединяющий начало вектора и конец вектора
и конец вектора ,
при условии, что конец вектора
,
при условии, что конец вектора совпадает с началом вектора
совпадает с началом вектора (правило
треугольника).
Произведением
вектора
(правило
треугольника).
Произведением
вектора
 на действительное число
на действительное число называется
вектор
называется
вектор
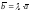 :
:1) коллинеарный вектору
 ;2)
имеющий длину
;2)
имеющий длину
 ;3)
направленный одинаково с вектором
;3)
направленный одинаково с вектором
 ,
если
,
если ,
и противоположно, если
,
и противоположно, если .
.Ортом вектора
 ,
называется вектор
,
называется вектор ,
имеющий единичную длину и направление
вектора
,
имеющий единичную длину и направление
вектора :
: .
.Базисом в пространстве
 называется упорядоченная тройка
некомпланарных векторов,базисом
на плоскости
называется упорядоченная тройка
некомпланарных векторов,базисом
на плоскости
 – упорядоченная пара неколлинеарных
векторов, базисом
на прямой
– упорядоченная пара неколлинеарных
векторов, базисом
на прямой
 –
любой ненулевой вектор на этой прямой.
Базис, в котором все векторы попарно
перпендикулярны и имеют единичную
длину, называетсяортонормированным.
Векторы ортонормированного базиса
обозначаются:
–
любой ненулевой вектор на этой прямой.
Базис, в котором все векторы попарно
перпендикулярны и имеют единичную
длину, называетсяортонормированным.
Векторы ортонормированного базиса
обозначаются:
 и
и ,
и называютсябазисными
ортами.
Различают правый и левый ортонормированные
базисы. Базис
,
и называютсябазисными
ортами.
Различают правый и левый ортонормированные
базисы. Базис
 -называется
правым, если кратчайший поворот от
-называется
правым, если кратчайший поворот от к
к совершается против хода часовой стрелки,
в противном случае он – левый. Базис
совершается против хода часовой стрелки,
в противном случае он – левый. Базис -называется
правым, если из конца вектора
-называется
правым, если из конца вектора кратчайший поворот от вектора
кратчайший поворот от вектора к
к виден совершающимся против хода часовой
стрелки, в противном случае он – левый.
виден совершающимся против хода часовой
стрелки, в противном случае он – левый.Условием коллинеарности векторов
 и
и является равенство:
является равенство: ,
где
,
где - некоторое число.Условием
компланарности векторов
- некоторое число.Условием
компланарности векторов
 ,
, и
и является равенство:
является равенство: ,
где
,
где - некоторые числа.
- некоторые числа.Всякий геометрический вектор может быть разложен единственным образом по векторам базиса, коэффициенты разложения называются при этом координатами вектора в данном базисе. Например, если
 - базис
- базис и
и ,
то всегда существует единственное
разложение:
,
то всегда существует единственное
разложение: ,
где числа
,
где числа - координаты вектора
- координаты вектора в базисе
в базисе ,
при этом пишут
,
при этом пишут .
Если в
.
Если в зафиксирован ортонормированный базис
зафиксирован ортонормированный базис и
и ,
то равносильны записи:
,
то равносильны записи: и
и (в записи
вектора в координатной форме
ортонормированный базис не указывают).
(в записи
вектора в координатной форме
ортонормированный базис не указывают).Представление геометрических векторов в координатной форме, позволяет выполнять действия над ними, как над арифметическими векторами:
 ;
; .
.Декартовой прямоугольной системой координат в пространстве называется совокупность точки
 (начало координат) и правого
ортонормированного базиса
(начало координат) и правого
ортонормированного базиса и обозначается
и обозначается .
Прямые
.
Прямые ,
, ,
, ,
проходящие через начало координат в
направлении базисных векторов, называютсякоординатными
осями:
первая – осью абсцисс, вторая – осью
ординат, третья – осью аппликат.
Плоскости, проходящие через оси
координат, называются координатными
плоскостями.
Аналогично вводится система координат
на плоскости:
,
проходящие через начало координат в
направлении базисных векторов, называютсякоординатными
осями:
первая – осью абсцисс, вторая – осью
ординат, третья – осью аппликат.
Плоскости, проходящие через оси
координат, называются координатными
плоскостями.
Аналогично вводится система координат
на плоскости:
 .
.Пусть
 - произвольная точка пространства, в
котором введена система координат
- произвольная точка пространства, в
котором введена система координат =
= .Радиус-вектором
точки
.Радиус-вектором
точки
 называется вектор
называется вектор ,
который всегда единственным образом
можно представить в виде:
,
который всегда единственным образом
можно представить в виде: .
Числа
.
Числа ,
являющиеся координатами радиус-вектора,
совпадают с проекциями вектора
,
являющиеся координатами радиус-вектора,
совпадают с проекциями вектора на базисные орты
на базисные орты и
и (на координатные оси
(на координатные оси и
и ).Координатами
точки
).Координатами
точки
 в системе координат
в системе координат называются координаты её радиус-вектора
называются координаты её радиус-вектора и пишут
и пишут .
В свою очередь, координаты точки
.
В свою очередь, координаты точки полностью определяют её радиус-вектор
полностью определяют её радиус-вектор .
Всякий геометрический вектор
.
Всякий геометрический вектор в системе координат
в системе координат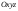 ,
всегда можно представить как радиус-вектор
некоторой точки и записать в виде:
,
всегда можно представить как радиус-вектор
некоторой точки и записать в виде: .
.Длина
 вектора
вектора ,
заданного координатами
,
заданного координатами ,
определяется формулой:
,
определяется формулой: .Направляющими
косинусами вектора
.Направляющими
косинусами вектора
 называются числа:
называются числа: ,
, ,
, ,
при этом
,
при этом .
.Координаты вектора
 ,
заданного точками
,
заданного точками и
и определяются по формуле:
определяются по формуле: .
Расстояние
.
Расстояние между точками
между точками и
и определяется как длина вектора
определяется как длина вектора и находится по формуле:
и находится по формуле: .
.Координаты точки
 делящей отрезок
делящей отрезок пополам находятся по формулам:
пополам находятся по формулам: ,
, ,
, .
.Скалярным произведением векторов
 и
и называется число
называется число .
Скалярное произведение обладает
свойствами:
.
Скалярное произведение обладает
свойствами:1)
 ;
2)
;
2) где
где
 -
число;
-
число; 3) ; 4)
5)
 ;
6)
;
6) ,
, ,
, ,
,
 ,
, ,
, .
Для векторов
.
Для векторов и
и ,
заданных своими координатами
,
заданных своими координатами ,
, скалярное произведение вычисляется
по формуле:
скалярное произведение вычисляется
по формуле: .
.Скалярное произведение применяют: 1) для вычисления угла между векторами
 и
и по формуле:
по формуле: ;2)
для вычисления проекции вектора
;2)
для вычисления проекции вектора
 на вектор
на вектор по формуле:
по формуле: ;3)
для вычисления длины вектора
;3)
для вычисления длины вектора
 по формуле:
по формуле: ;4)
в качестве условия перпендикулярности
векторов
;4)
в качестве условия перпендикулярности
векторов
 и
и :
: .
.Векторным произведением векторов
 и
и называется вектор
называется вектор ,
определяемый условиями:1)
,
определяемый условиями:1) ;
;
2)
 и
и ;3)
;3)
 - правая тройка векторов.
- правая тройка векторов.Упорядоченная тройка
 некомпланарных векторов называетсяправой
тройкой,
если из конца третьего вектора
некомпланарных векторов называетсяправой
тройкой,
если из конца третьего вектора
 ,
кратчайший поворот от первого вектора
,
кратчайший поворот от первого вектора ко второму
ко второму ,
виден совершающимся против хода часовой
стрелки. В противном случае, тройка
,
виден совершающимся против хода часовой
стрелки. В противном случае, тройка называется левой.
называется левой.Векторное произведение обладает свойствами:
1)
 ;
2)
;
2) ,где
,где
 -
число;
-
число; 3) ; 4)5);
6)
 ,
, ,
,
 ,
, ,
, ,
, .
.Для векторов
 и
и ,
заданных своими координатами
,
заданных своими координатами ,
, векторное произведение вычисляется
по формуле:
векторное произведение вычисляется
по формуле: .
.Векторное произведение
 применяют:1)
для вычисления площадей треугольника
и параллелограмма, построенных на
векторах
применяют:1)
для вычисления площадей треугольника
и параллелограмма, построенных на
векторах
 и
и ,
как на сторонах, по формуле:
,
как на сторонах, по формуле: ;2)
в качестве условия параллельности
векторов
;2)
в качестве условия параллельности
векторов
 и
и :
: .
.Смешанным произведением упорядоченной тройки векторов
 ,
, и
и называется число
называется число .
.Смешанное произведение обладает свойствами:
1) ; 2);
3)
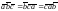 ;
4)
;
4) и
и
 -компланарны
-компланарны
 ;
;5)
 ,где
,где
 -объём
параллелепипеда, построенного на
векторах
-объём
параллелепипеда, построенного на
векторах ,
, и
и .
.
Для векторов
 ,
, и
и ,
заданных своими координатами
,
заданных своими координатами ,
, ,
, смешанное произведение вычисляется
по формуле:
смешанное произведение вычисляется
по формуле: .
.Смешанное произведение
 применяют:1)
для вычисления объёмов тетраэдра и
параллелепипеда, построенных на векторах
применяют:1)
для вычисления объёмов тетраэдра и
параллелепипеда, построенных на векторах
 ,
, и
и ,
как на рёбрах, по формуле:
,
как на рёбрах, по формуле: ;2)
в качестве условия компланарности
векторов
;2)
в качестве условия компланарности
векторов
 ,
, и
и :
: и
и -
компланарны.
-
компланарны.Тема 5. Прямые линии и плоскости.
Нормальным вектором прямой
 ,
называется всякий ненулевой вектор
,
называется всякий ненулевой вектор
 перпендикулярный данной прямой.Направляющим
вектором прямой
перпендикулярный данной прямой.Направляющим
вектором прямой
 ,
называется всякий ненулевой вектор
,
называется всякий ненулевой вектор параллельный данной прямой.
параллельный данной прямой.Прямая
 на
плоскости
в системе координат
на
плоскости
в системе координат
 может быть задана уравнением одного
из следующих видов:
может быть задана уравнением одного
из следующих видов:1)
 -общее
уравнение
прямой, где
-общее
уравнение
прямой, где
 - нормальный вектор прямой;
- нормальный вектор прямой;2)
 - уравнение прямой, проходящей через
точку
- уравнение прямой, проходящей через
точку перпендикулярно данному вектору
перпендикулярно данному вектору ;
;3)
 - уравнение прямой, проходящей через
точку
- уравнение прямой, проходящей через
точку параллельно данному вектору
параллельно данному вектору (каноническое
уравнение);
(каноническое
уравнение);
4)
 - уравнение прямой, проходящей через
две данные точки
- уравнение прямой, проходящей через
две данные точки ,
, ;
;5)
 -уравнения
прямой с
угловым коэффициентом
-уравнения
прямой с
угловым коэффициентом
 ,
где
,
где
 - точка через которую прямая проходит;
- точка через которую прямая проходит; (
( )
– угол, который прямая составляет с
осью
)
– угол, который прямая составляет с
осью ;
; -
длина отрезка (со знаком
-
длина отрезка (со знаком ),
отсекаемого прямой на оси
),
отсекаемого прямой на оси (знак «
(знак « »,
если отрезок отсекается на положительной
части оси и «
»,
если отрезок отсекается на положительной
части оси и « »,
если на отрицательной).
»,
если на отрицательной).6)
 -уравнение
прямой в
отрезках, где
-уравнение
прямой в
отрезках, где
 и
и -
длины отрезков (со знаком
-
длины отрезков (со знаком ),
отсекаемых прямой на координатных осях
),
отсекаемых прямой на координатных осях и
и (знак «
(знак « »,
если отрезок отсекается на положительной
части оси и «
»,
если отрезок отсекается на положительной
части оси и « »,
если на отрицательной).
»,
если на отрицательной).Расстояние от точки
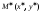 до прямой
до прямой ,
заданной общим уравнением
,
заданной общим уравнением на плоскости, находится по формуле:
на плоскости, находится по формуле: .
.Угол
 ,(
,( )
между прямыми
)
между прямыми
 и
и ,
заданными общими уравнениями или
уравнениями с угловым коэффициентом,
находится по одной из следующих формул:
,
заданными общими уравнениями или
уравнениями с угловым коэффициентом,
находится по одной из следующих формул: ;
;
 .
. ,
если
,
если
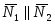
 или
или .
. ,если
,если
 или
или
Координаты точки пересечения прямых
 и
и находятся как решение системы линейных
уравнений:
находятся как решение системы линейных
уравнений: или
или .
.Нормальным вектором плоскости
 ,
называется всякий ненулевой вектор
,
называется всякий ненулевой вектор перпендикулярный данной плоскости.
перпендикулярный данной плоскости.Плоскость
 в системе координат
в системе координат
 может быть задана уравнением одного
из следующих видов:
может быть задана уравнением одного
из следующих видов:1)
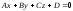 -общее
уравнение
плоскости, где
-общее
уравнение
плоскости, где
 - нормальный вектор плоскости;
- нормальный вектор плоскости;2)
 - уравнение плоскости, проходящей через
точку
- уравнение плоскости, проходящей через
точку перпендикулярно данному вектору
перпендикулярно данному вектору ;
;3)
 - уравнение плоскости, проходящей через
три точки
- уравнение плоскости, проходящей через
три точки ,
, и
и ;
;4)
 -уравнение
плоскости в
отрезках, где
-уравнение
плоскости в
отрезках, где
 ,
, и
и - дины отрезков (со знаком
- дины отрезков (со знаком ),
отсекаемых плоскостью на координатных
осях
),
отсекаемых плоскостью на координатных
осях ,
, и
и (знак «
(знак « »,
если отрезок отсекается на положительной
части оси и «
»,
если отрезок отсекается на положительной
части оси и « »,
если на отрицательной).
»,
если на отрицательной).Расстояние от точки
 до плоскости
до плоскости ,
заданной общим уравнением
,
заданной общим уравнением ,
находится по формуле:
,
находится по формуле: .
.Угол
 ,(
,( )
между плоскостями
)
между плоскостями
 и
и
 ,
заданными общими уравнениями, находится
по формуле:
,
заданными общими уравнениями, находится
по формуле: .
. ,
если
,
если


 ,
если
,
если
 .
.Прямая
 в
пространстве
в системе координат
в
пространстве
в системе координат
 может быть задана уравнением одного
из следующих видов:
может быть задана уравнением одного
из следующих видов:1)
 -общее
уравнение
прямой, как линии пересечения двух
плоскостей, где
-общее
уравнение
прямой, как линии пересечения двух
плоскостей, где
 и
и -
нормальные векторы плоскостей
-
нормальные векторы плоскостей и
и ;
;2)
 - уравнение прямой, проходящей через
точку
- уравнение прямой, проходящей через
точку параллельно данному вектору
параллельно данному вектору (каноническое
уравнение);
(каноническое
уравнение);
3)
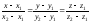 - уравнение прямой, проходящей через
две данные точки
- уравнение прямой, проходящей через
две данные точки ,
, ;
;4)
 -уравнение
прямой, проходящей через точку
-уравнение
прямой, проходящей через точку
 параллельно данному вектору
параллельно данному вектору ,
, (параметрическое
уравнение);
(параметрическое
уравнение);
Угол
 ,(
,( )между
прямыми
)между
прямыми
 и
и в пространстве,
заданными каноническими уравнениями
находится по формуле:
в пространстве,
заданными каноническими уравнениями
находится по формуле:  .
. ,
если
,
если


 .
. ,
если
,
если
 .
.Координаты точки пересечения прямой
 ,
заданной параметрическим уравнениеми плоскости
,
заданной параметрическим уравнениеми плоскости
 ,
заданной общим уравнением, находятся
как решение системы линейных уравнений:
,
заданной общим уравнением, находятся
как решение системы линейных уравнений: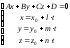 .
.Угол
 ,(
,( )между
прямой
)между
прямой
 ,
заданной каноническим уравнениеми
плоскостью
,
заданной каноническим уравнениеми
плоскостью
 ,
заданной общим уравнением находится
по формуле:
,
заданной общим уравнением находится
по формуле: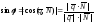 .
. ,
если
,
если




 .
. ,
если
,
если


 .
.Тема 6. Кривые второго порядка.
Алгебраической кривой второго порядка в системе координат
 называется кривая
называется кривая ,общее
уравнение
которой имеет вид:
,общее
уравнение
которой имеет вид:  ,
,где числа
 -
не равны нулю одновременно. Существует
следующая классификация кривых второго
порядка:1)
если
-
не равны нулю одновременно. Существует
следующая классификация кривых второго
порядка:1)
если
 ,
то общее уравнение определяет кривуюэллиптического
типа
(окружность (при
,
то общее уравнение определяет кривуюэллиптического
типа
(окружность (при
 ),
эллипс (при
),
эллипс (при ),
пустое множество, точку);2)
если
),
пустое множество, точку);2)
если
 ,
то - кривуюгиперболического
типа
(гиперболу, пару пересекающихся прямых);
3)
если
,
то - кривуюгиперболического
типа
(гиперболу, пару пересекающихся прямых);
3)
если
 ,
то - кривуюпараболического
типа
(параболу, пустое множество, прямую,
пару параллельных прямых) . Окружность,
эллипс, гипербола и парабола называются
невырожденными
кривыми второго порядка.
,
то - кривуюпараболического
типа
(параболу, пустое множество, прямую,
пару параллельных прямых) . Окружность,
эллипс, гипербола и парабола называются
невырожденными
кривыми второго порядка.Общее уравнение
 ,
где
,
где ,
определяющее невырожденную кривую
(окружность, эллипс, гиперболу, параболу),
всегда (методом выделения полных
квадратов) можно привести к уравнению
одного из следующих видов:
,
определяющее невырожденную кривую
(окружность, эллипс, гиперболу, параболу),
всегда (методом выделения полных
квадратов) можно привести к уравнению
одного из следующих видов:1а)
 -уравнение
окружности с центром в точке
-уравнение
окружности с центром в точке
 и радиусом
и радиусом (рис. 5).
(рис. 5).1б)
 - уравнение эллипса с центром в точке
- уравнение эллипса с центром в точке
 и осями симметрии, параллельными
координатным осям. Числа
и осями симметрии, параллельными
координатным осям. Числа и
и - называютсяполуосями
эллипса;
прямоугольник со сторонами
- называютсяполуосями
эллипса;
прямоугольник со сторонами
 ,
, параллельными осям симметрии и центром
в точке
параллельными осям симметрии и центром
в точке -основным
прямоугольником эллипса; точки
пересечения основного прямоугольника
с осями симметрии - вершинами
эллипса.
-основным
прямоугольником эллипса; точки
пересечения основного прямоугольника
с осями симметрии - вершинами
эллипса.
Для построения эллипса в системе координат
 :1)
отмечаем центр
:1)
отмечаем центр
 эллипса;2)
проводим через центр пунктирной линией
оси симметрии эллипса; 3)
строим пунктиром основной прямоугольник
эллипса с центром
эллипса;2)
проводим через центр пунктирной линией
оси симметрии эллипса; 3)
строим пунктиром основной прямоугольник
эллипса с центром
 и сторонами
и сторонами ,
, параллельными осям симметрии;4)
изображаем сплошной линией эллипс,
вписывая его в основной прямоугольник
так, чтобы эллипс касался его сторон
только в вершинах эллипса (рис.6) .
параллельными осям симметрии;4)
изображаем сплошной линией эллипс,
вписывая его в основной прямоугольник
так, чтобы эллипс касался его сторон
только в вершинах эллипса (рис.6) . Аналогично строится и окружность, основной прямоугольник которой имеет стороны
 (рис. 5).
(рис. 5).
Рис.5 Рис 6
2)
 - уравнения гипербол (называемых
сопряжёнными)
с центром в точке
- уравнения гипербол (называемых
сопряжёнными)
с центром в точке
 и осями симметрии, параллельными
координатным осям. Числа
и осями симметрии, параллельными
координатным осям. Числа и
и - называютсяполуосями
гипербол;
прямоугольник со сторонами
- называютсяполуосями
гипербол;
прямоугольник со сторонами
 ,
, параллельными осям симметрии и центром
в точке
параллельными осям симметрии и центром
в точке -основным
прямоугольником гипербол; точки
пересечения основного прямоугольника
с осями симметрии - вершинами
гипербол; прямые
-основным
прямоугольником гипербол; точки
пересечения основного прямоугольника
с осями симметрии - вершинами
гипербол; прямые
 ,
проходящие через противоположные
вершины основного прямоугольника –асимптотами
гипербол.
,
проходящие через противоположные
вершины основного прямоугольника –асимптотами
гипербол.
Для построения гиперболы в системе координат
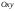 :1)
отмечаем центр гиперболы
:1)
отмечаем центр гиперболы
 ;2)
проводим через центр
;2)
проводим через центр
 пунктирной линией оси симметрии
гиперболы;3)
строим пунктиром основной прямоугольник
гиперболы с центром
пунктирной линией оси симметрии
гиперболы;3)
строим пунктиром основной прямоугольник
гиперболы с центром
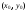 и сторонами
и сторонами и
и параллельными осям симметрии;4)
проводим
через противоположные вершины основного
прямоугольника пунктирной линией
прямые, являющиеся асимптотами гиперболы,
к которым неограниченно близко, при
бесконечном удалении от начала координат,
приближаются ветви гиперболы, не
пересекая их; 5)
изображаем сплошной линией ветви
гиперболы
параллельными осям симметрии;4)
проводим
через противоположные вершины основного
прямоугольника пунктирной линией
прямые, являющиеся асимптотами гиперболы,
к которым неограниченно близко, при
бесконечном удалении от начала координат,
приближаются ветви гиперболы, не
пересекая их; 5)
изображаем сплошной линией ветви
гиперболы
 (рис. 7) или гиперболы
(рис. 7) или гиперболы (рис. 8).
(рис. 8).
Рис.7 Рис.8
3а)
 - уравнение параболы с вершиной в точке
- уравнение параболы с вершиной в точке и осью симметрии, параллельной
координатной оси
и осью симметрии, параллельной
координатной оси (рис. 9).
(рис. 9).3б)
 - уравнение параболы с вершиной в точке
- уравнение параболы с вершиной в точке
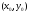 и осью симметрии, параллельной
координатной оси
и осью симметрии, параллельной
координатной оси (рис. 10).
(рис. 10).Для построения параболы в системе координат
 :1)
отмечаем вершину параболы
:1)
отмечаем вершину параболы
 ;2)
проводим через вершину
;2)
проводим через вершину
 пунктирной линией ось симметрии
параболы;3)
изображаем сплошной линией параболу,
направляя её ветвь, с учётом знака
параметра параболы
пунктирной линией ось симметрии
параболы;3)
изображаем сплошной линией параболу,
направляя её ветвь, с учётом знака
параметра параболы
 :
при
:
при -
в положительную сторону координатной
оси, параллельной оси симметрии параболы
(рис. 9а и 10а); при
-
в положительную сторону координатной
оси, параллельной оси симметрии параболы
(рис. 9а и 10а); при - в отрицательную сторону координатной
оси (рис.9б и 10б) .
- в отрицательную сторону координатной
оси (рис.9б и 10б) .
Рис. 9а Рис. 9б

Рис. 10а Рис. 10б
Тема 7. Множества. Числовые множества. Функция.
Под множеством понимают некоторую совокупность объектов любой природы, различимых между собой и мыслимую как единое целое. Объекты, составляющие множество называют его элементами. Множество может быть бесконечным (состоит из бесконечного числа элементов), конечным (состоит из конечного числа элементов), пустым (не содержит ни одного элемента). Множества обозначают:
 ,
а их элементы:
,
а их элементы: .
Пустое множество обозначают
.
Пустое множество обозначают .
.Множество
 называютподмножеством
множества
называютподмножеством
множества
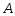 ,
если все элементы множества
,
если все элементы множества принадлежат множеству
принадлежат множеству и пишут
и пишут .
Множества
.
Множества и
и называютравными,
если они состоят из одних и тех же
элементов и пишут
называютравными,
если они состоят из одних и тех же
элементов и пишут
 .
Два множества
.
Два множества и
и будут равны тогда и только тогда, когда
будут равны тогда и только тогда, когда и
и .
.Множество
 называютуниверсальным
(в рамках
данной математической теории),
если его
элементами являются все объекты,
рассматриваемые в данной теории.
называютуниверсальным
(в рамках
данной математической теории),
если его
элементами являются все объекты,
рассматриваемые в данной теории. Множество можно задать: 1) перечислением всех его элементов, например:
 (только для конечных множеств);2)
заданием правила
(только для конечных множеств);2)
заданием правила
 определения принадлежности элемента
определения принадлежности элемента универсального множества
универсального множества ,
данному множеству
,
данному множеству :
: .
.Объединением множеств
 и
и называется множество
называется множество .
.Пересечением множеств
 и
и называется множество
называется множество .
.Разностью множеств
 и
и называется множество
называется множество .
.Дополнением множества
 (до универсального множества
(до универсального множества )
называется множество
)
называется множество .
.Два множества
 и
и называютсяэквивалентными
и пишут
называютсяэквивалентными
и пишут
 ~
~ ,
если между элементами этих множеств
может быть установлено взаимно
однозначное соответствие. Множество
,
если между элементами этих множеств
может быть установлено взаимно
однозначное соответствие. Множество называетсясчётным,
если оно эквивалентно множеству
натуральных чисел
называетсясчётным,
если оно эквивалентно множеству
натуральных чисел
 :
: ~
~ .
Пустое множество по определению
относится к счётным.
.
Пустое множество по определению
относится к счётным.Понятие мощности множества возникает при сравнении множеств по числу содержащихся в них элементов. Мощность множества
 обозначают
обозначают .
Мощностью конечного множества является
число его элементов.
.
Мощностью конечного множества является
число его элементов.Эквивалентные множества обладают равной мощностью. Множество
 называетсянесчётным,
если его мощность больше мощности
множества
называетсянесчётным,
если его мощность больше мощности
множества
 .
.Действительным (вещественным) числом называется бесконечная десятичная дробь, взятая со знаком «+» или «
 ».
Действительные числа отождествляют с
точками числовой прямой.Модулем
(абсолютной величиной) действительного
числа
».
Действительные числа отождествляют с
точками числовой прямой.Модулем
(абсолютной величиной) действительного
числа
 называется неотрицательное число:
называется неотрицательное число:
Множество
 называетсячисловым,
если его элементами
называетсячисловым,
если его элементами
 являются действительные числа.Числовымипромежутками
называются множества чисел:
являются действительные числа.Числовымипромежутками
называются множества чисел: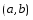 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
.Множество всех точек
 на числовой прямой, удовлетворяющих
условию
на числовой прямой, удовлетворяющих
условию ,
где
,
где - сколь угодно малое число, называется
- сколь угодно малое число, называется -окрестностью
(или просто
окрестностью) точки
-окрестностью
(или просто
окрестностью) точки
 и обозначается
и обозначается .
Множество всех точек
.
Множество всех точек условием
условием ,
где
,
где - сколь угодно большое число, называется
- сколь угодно большое число, называется -окрестностью
(или просто окрестностью) бесконечности
и обозначается
-окрестностью
(или просто окрестностью) бесконечности
и обозначается
 .
.Величина, сохраняющая одно и тоже числовое значение, называется постоянной. Величина, принимающая различные числовые значения, называется переменной. Функцией
 называется правило, по которому каждому
числу
называется правило, по которому каждому
числу
 ставится в соответствие одно вполне
определённое число
ставится в соответствие одно вполне
определённое число ,
и пишут
,
и пишут .
Множество
.
Множество называетсяобластью
определения
функции,
называетсяобластью
определения
функции,
 -множеством
(или областью)
значений
функции,
-множеством
(или областью)
значений
функции,
 -аргументом,
-аргументом,
 -значением
функции.
Наиболее
распространённым способом задания
функции является аналитический способ,
при котором функция задаётся формулой.
Естественной
областью определения
функции
-значением
функции.
Наиболее
распространённым способом задания
функции является аналитический способ,
при котором функция задаётся формулой.
Естественной
областью определения
функции
 называется множество
называется множество значений аргумента
значений аргумента ,
для которого данная формула имеет
смысл.Графиком
функции
,
для которого данная формула имеет
смысл.Графиком
функции
 ,
, в прямоугольной системе координат
в прямоугольной системе координат ,
называется множество всех точек
плоскости с координатами
,
называется множество всех точек
плоскости с координатами ,
, .
.Функция
 называетсячётной
на множестве
называетсячётной
на множестве
 ,
симметричном относительно точки
,
симметричном относительно точки ,
если для всех
,
если для всех выполняется условие:
выполняется условие: инечётной,
если выполняется условие
инечётной,
если выполняется условие
 .
В противном случае
.
В противном случае -
функция общего вида илини
чётная, ни нечётная.
-
функция общего вида илини
чётная, ни нечётная.
Функция
 называетсяпериодической
на множестве
называетсяпериодической
на множестве
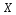 ,
если существует число
,
если существует число (период
функции),
такое, что для всех
(период
функции),
такое, что для всех
 выполняется условие:
выполняется условие: .
Наименьшее число
.
Наименьшее число называется основным периодом.
называется основным периодом.Функция
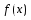 называетсямонотонно
возрастающей
(убывающей)
на множестве
называетсямонотонно
возрастающей
(убывающей)
на множестве
 ,
если большему значению аргумента
,
если большему значению аргумента соответствует большее (меньшее) значение
функции
соответствует большее (меньшее) значение
функции .
.Функция
 называетсяограниченной
на множестве
называетсяограниченной
на множестве
 ,
если существует число
,
если существует число ,
такое, что для всех
,
такое, что для всех выполняется условие:
выполняется условие: .
В противном случае функция -неограниченная.
.
В противном случае функция -неограниченная.Обратной к функции
 ,
, ,
,
 называется
такая функция
называется
такая функция
 ,
которая определена на множестве
,
которая определена на множестве и каждому
и каждому ставит
в соответствие такое
ставит
в соответствие такое
 ,
что
,
что .
Для нахождения функции
.
Для нахождения функции ,
обратной к функции
,
обратной к функции ,
нужно решить
уравнение
,
нужно решить
уравнение
 относительно
относительно
 .
Если функция
.
Если функция
 ,
, является строго монотонной на
является строго монотонной на
 ,
то она всегда имеет обратную, при этом,
если функция
возрастает
(убывает), то обратная функция также
возрастает (убывает).
,
то она всегда имеет обратную, при этом,
если функция
возрастает
(убывает), то обратная функция также
возрастает (убывает). Функция
 ,
представляемая в виде
,
представляемая в виде ,
где
,
где ,
, -
некоторые функции такие, что область
определения функции
-
некоторые функции такие, что область
определения функции содержит всё множество значений функции
содержит всё множество значений функции ,
называетсясложной
функцией
независимого аргумента
,
называетсясложной
функцией
независимого аргумента
 .
Переменную
.
Переменную называют при этом промежуточным
аргументом. Сложную функцию
называют при этом промежуточным
аргументом. Сложную функцию называют также композицией функций
называют также композицией функций и
и ,
и пишут:
,
и пишут: .
.Основными элементарными функциями считаются: степенная функция
 ,показательная
функция
,показательная
функция
 (
( ,
, ),логарифмическая
функция
),логарифмическая
функция
 (
( ,
, ),тригонометрические
функции
),тригонометрические
функции
 ,
, ,
,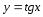 ,
, ,обратные
тригонометрические
функции
,обратные
тригонометрические
функции
 ,
, ,
, ,
, .Элементарной
называется
функция, полученная из основных
элементарных функций конечным числом
их арифметических операций и композиций.
.Элементарной
называется
функция, полученная из основных
элементарных функций конечным числом
их арифметических операций и композиций.Если задан график
 функции
функции
 ,
, ,
то построение графика функции
,
то построение графика функции сводится к ряду преобразований (сдвиг,
сжатие или растяжение, отображение)
графика
сводится к ряду преобразований (сдвиг,
сжатие или растяжение, отображение)
графика :
:1) преобразование
 симметрично отображает график
симметрично отображает график ,
относительно оси
,
относительно оси ;2)
преобразование
;2)
преобразование
 симметрично отображает график
симметрично отображает график ,
относительно оси
,
относительно оси ;3)
преобразование
;3)
преобразование
 сдвигает график
сдвигает график по оси
по оси на
на единиц (
единиц (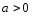 -
вправо,
-
вправо, - влево);4)
преобразование
- влево);4)
преобразование
 сдвигает график
сдвигает график по оси
по оси на
на единиц (
единиц ( -
вверх,
-
вверх, - вниз);5)
преобразование
- вниз);5)
преобразование
 график
график вдоль оси
вдоль оси растягивает в
растягивает в раз, если
раз, если или сжимает в
или сжимает в раз, если
раз, если ;6)
преобразование
;6)
преобразование
 график
график вдоль оси
вдоль оси сжимает в
сжимает в раз, если
раз, если или растягивает в
или растягивает в раз, если
раз, если .
.Последовательность преобразований при построении графика функции
 можно представить символически в виде:
можно представить символически в виде:


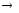




 .
.Примечание. При выполнении преобразования
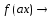
 следует иметь в виду, что величина
сдвига вдоль оси
следует иметь в виду, что величина
сдвига вдоль оси определяется той константой, которая
прибавляется непосредственно к аргументу
определяется той константой, которая
прибавляется непосредственно к аргументу ,
а не к аргументу
,
а не к аргументу .
.Графиком функции
 является парабола с вершиной в точке
является парабола с вершиной в точке ,
ветви которой направлены вверх, если
,
ветви которой направлены вверх, если или вниз, если
или вниз, если .
Графиком дробно-линейной функции
.
Графиком дробно-линейной функции является гипербола с центром в точке
является гипербола с центром в точке ,
асимптоты которой проходят через центр,
параллельно осям координат.
,
асимптоты которой проходят через центр,
параллельно осям координат.В некоторых случаях при построении графика функции целесообразно разбить её область определения на несколько непересекающихся промежутков и последовательно строить график на каждом из них. Например, при построении графика функции, в аналитическое выражение которой входит функция
 ,
следует выделить и рассмотреть отдельно
промежутки, на которых выражение под
знаком модуля не меняет знак.
,
следует выделить и рассмотреть отдельно
промежутки, на которых выражение под
знаком модуля не меняет знак.График функции
 можно построить, предварительно построив
графики функций
можно построить, предварительно построив
графики функций и
и ,
а затем сложив их ординаты при одинаковых
значениях
,
а затем сложив их ординаты при одинаковых
значениях .
.Тема 8. Предел функции. Эквивалентные функции.
Число
![]() называетсяпределом
функции
называетсяпределом
функции
![]() при
при
![]() (или в точке
(или в точке
![]() ),
и пишут
),
и пишут![]() ,
если для любого числа
,
если для любого числа![]() найдётся число
найдётся число![]() такое, что при всех
такое, что при всех![]() ,
удовлетворяющих условию
,
удовлетворяющих условию![]() ,
выполняется неравенство
,
выполняется неравенство![]() .
.
Число
![]() называетсяпределом
функции
называетсяпределом
функции
![]() при
при
![]() ,
и пишут
,
и пишут
![]() ,
если для любого числа
,
если для любого числа![]() найдётся число
найдётся число![]() такое, что при всех
такое, что при всех![]() ,
удовлетворяющих условию
,
удовлетворяющих условию![]() ,
выполняется неравенство
,
выполняется неравенство![]() .
.
Рассматривают
также односторонние пределы функций:
![]() ,
,![]() ,
,![]() ,
,![]() ,
где
,
где![]() стремится к
стремится к![]() ,
,![]() ,
,![]() или только с левой стороны или только
с правой стороны.
или только с левой стороны или только
с правой стороны.
Основные
утверждения, используемые для вычисления
пределов функций при
![]() (в дальнейшем
(в дальнейшем![]() -
или число
-
или число![]() или символ
или символ![]() ):
):
1)
Если
![]() - постоянная величина, то
- постоянная величина, то![]() .
.
2) Если существуют конечные пределы
 ,
, ,
то:
,
то:а)
 ;б)
;б)
 ;
;в)

 ;г)
;г)
 ,
если
,
если .
.
При
вычислении пределов постоянно пользуются
и тем, что для любой основной элементарной
функции
![]() и точки
и точки![]() из её области определения справедливо
соотношение
из её области определения справедливо
соотношение![]() .
.
Функция
![]() называетсябесконечно
большой
при
называетсябесконечно
большой
при
![]() ,
если
,
если![]() .
Функция
.
Функция![]() называетсябесконечно
малой при
называетсябесконечно
малой при
![]() ,
если
,
если![]() .
.
Основные
утверждения для бесконечно больших
функций, используемые для вычисления
пределов при
![]() :
:
1) Если
 ,
то
,
то ,если
,если ,
то
,
то
2) Если
 и
и ,
то
,
то .
.
3)
Если
![]() и
и![]() ,
то
,
то![]() .
.
4)
Если
![]() и
и![]() ,
то
,
то![]() .
.
5)
Если
![]() и
и![]() ,
то
,
то![]() .
.
6)
Если
![]() и
и![]() ,
то
,
то![]() .
.
Если
непосредственное применение свойств
конечных пределов и бесконечно больших
функций приводит к неопределённым
выражениям, символически обозначаемым:
![]() ,
то для вычисления предела – «раскрытия
неопределённости» - преобразовывают
выражение так, чтобы получить возможность
его вычислить.
,
то для вычисления предела – «раскрытия
неопределённости» - преобразовывают
выражение так, чтобы получить возможность
его вычислить.
Первым
замечательным пределом
называется предел:
![]() .
Следствиями из него являются пределы:
.
Следствиями из него являются пределы:
![]() ,
,
![]() ,
,![]()
Вторым замечательным пределом называются пределы:
![]()
![]() ,
,
где
![]() -основание
натуральных логарифмов (число Непера).
Он используется для вычисления предела
степенно-показательной функции
-основание
натуральных логарифмов (число Непера).
Он используется для вычисления предела
степенно-показательной функции![]() ,
где
,
где![]() и
и![]() .
.
При
нахождении пределов
![]() следует иметь в виду:
следует иметь в виду:
1)
Если
![]() ,
,![]() ,
то
,
то![]() .
.
2)
Если
![]() ,
,![]() ,
то
,
то![]() вычисляют, учитывая, что:
вычисляют, учитывая, что: ,
, .
.
