
- •Федеральное агентство по образованию
- •1.Цель и задачи дисциплины, её место в учебном процессе.
- •Задачи изучения дисциплины. Требования к знаниям и умениям студента.
- •2. Содержание и структура дисциплины.
- •Раздел III. Аналитическая геометрия
- •Тема 5. Прямые линии и плоскости.
- •Тема 6. Кривые и поверхности второго порядка
- •Дополнительная литература:
- •4. Методические указания по изучению дисциплины.
- •5. Материалы для контроля знаний студентов.
- •3.1. 3.2.
- •Раздел II. Векторная алгебра.
- •Раздел III. Аналитическая геометрия.
- •Раздел IV. Введение в анализ.
- •Раздел V. Комплексные числа. Алгебра многочленов.
- •6. Приложения.
- •6.1. Образец решения контрольных задач типового варианта.
- •, .
- •6.2. Краткие теоретические сведения.
- •Тема 1. Определители.
- •Тема 2. Матрицы.
- •Тема 3. Системы линейных уравнений.
- •Тема 4. Векторная алгебра.
- •3) ; 4)
- •3) ; 4)5);
- •1) ; 2);
- •Тема 5. Прямые линии и плоскости.
- •Тема 6. Кривые второго порядка.
- •Тема 7. Множества. Числовые множества. Функция.
- •Тема 8. Предел функции. Эквивалентные функции.
- •Тема 9. Непрерывность функции.
- •Тема 10. Комплексные числа и многочлены.
- •6.3 Образец оформления обложки с контрольной работой.
После проверки контрольная работа предъявляется к защите. На защите студент должен показать свое умение решать задачи, подобные тем, что имеются в его контрольной работе.
Образец решения типового варианта контрольной работы приведён в Приложении 1.
5. Материалы для контроля знаний студентов.
Итоговой формой контроля знаний является экзамен в конце семестра обучения. На экзамене студент должен показать знание теоретических основ курса в объёме вопросов, приведённых в разделе 5.2 и умение решать задачи, подобные тем, что имеются в его контрольной работе.
5.1. Задания для контрольной работы.
1.1 – 30. Вычислить определитель:
а) непосредственным разложением по
 строке;
строке;б) непосредственным разложением по
 столбцу.
столбцу.1.1
 1.2.
1.2. 1.3.
1.3.


 .
.
 .
.1.4.
 1.5.
1.5.
 1.6.
1.6.

 .
.


1.7.
 1.8.
1.8. 1.9.
1.9.

 .
.
 .
.
1.10.
 1.11.
1.11. 1.12.
1.12.
 .
.


1.13.
 1.14.
1.14. 1.15.
1.15.
 .
.


1.16.
 1.17.
1.17. 1.18.
1.18.




1.19.
 1.20.
1.20. 1.21.
1.21.
 .
.
 .
.
1.22.
 1.23.
1.23. 1.24
.
1.24
.
.
 .
.

1.25.
 1.26.
1.26.
 1.27.
1.27.



1.28.
 1.29.
1.29. 1.30.
1.30.



2.1 – 30. Найти: а) матрицу
 ,
если
,
если
 ;
;2.1.

 ,
,
 2.2.
2.2.



2.3.

 ,
,
 2.4.
2.4.
 ,
,

2.5.

 ,
,
 2.6.
2.6.
 ,
,

2.7.

 ,
,
 2.8.
2.8.
 ,
,

2.9.

 ,
,
 2.10.
2.10.
 ,
,

2.11.

 ,
,
 2.12.
2.12.
 ,
,

2.13.

 ,
,
 2.14.
2.14.
 ,
,


2.15.

 ,
,
 2.16.
2.16.
 ,
,

2.17.

 ,
,
 2.18.
2.18.
 ,
,

2.19.

 ,
,
 2.20.
2.20.
 ,
,

2.21.

 ,
,
 2.22.
2.22.
 ,
,

2.23.

 ,
,
 2.24.
2.24.

 ,
,

2.25.

 ,
,
 2.26.
2.26.

 ,
,

2.27.

 ,
,
 2.28.
2.28.

 ,
,

2.29.

 ,
,
 2.30.
2.30.

 ,
,

3.1 – 30.Дана система трех линейных уравнений с тремя неизвестными. Требуется: а) найти решение системы методом Крамера;
б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса.
3.1. 3.2.
3.3.
 3.4.
3.4.
3.5.
 3.6.
3.6.
3.7.
 3.8.
3.8.
3.9.
 3.10.
3.10.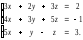
3.11.
 3.12.
3.12.

3.13.
 3.14.
3.14.

3.15.
 3.
16.
3.
16.

3.17.
 3.18.
3.18.
3.19.
 3.20.
3.20.
3.21.
 3.22.
3.22.
3.23.
 3.24.
3.24.
3.25.
 3.26.
3.26.
3.27.
 3.28.
3.28.
3.29
 3.30
3.30
4.1–30. Найти общее решение для каждой из данных систем методом Гаусса:
4.1 а)
 б)
б)
4.2 а)
 б)
б)
4.3 а)
 б)
б)
4.4 а)
 б)
б)
4.5 а)
 б)
б)
4.6 а)
 б)
б)
4.7 а)
 б)
б)
4.8 а)
 б)
б)
4.9 а)
 б)
б)
4.10 а)
 б)
б) 4.11 а)
4.11 а) б)
б) 4.12 а)
4.12 а) б)
б)
4.13 а)
 б)
б)
4.14 а)
 б)
б)
4.15 а)
 б)
б)
4.16 а)
 б)
б)
4.17 а)
 б)
б)
4.18 а)
 б)
б)
4.19 а)
 б)
б) 4.20 а)
4.20 а) б)
б)
4.21 а)
 б)
б)
4.22 а)
 б)
б)
4.23 а)
 б)
б)
4.24 а)
 б)
б) 4.25 а)
4.25 а) б)
б)
4.26 а)
 б)
б)
4.27 а)
 б)
б)
4.28 а)
 б)
б)
4.29 а)
 б)
б)
4.30 а)
 б)
б)
5.1 – 30. Даны векторы
 .
Требуется:
.
Требуется:а) вычислить скалярное произведение векторов
 ,
если
,
если
 ,
, ;
б)вычислить
векторное произведение векторов
;
б)вычислить
векторное произведение векторов
 ;в)
показать,
что векторы
;в)
показать,
что векторы
 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора в этом базисе.
в этом базисе.5.1
 ,
,
 ,
,
 ,
, .
.5.2.
 ,
,
 ,
,
 ,
, .
.5.3.




5.4.




5.5.




5.6.




5.7.




5.8.




5.9.

5.10.

5.11.




5.12.




5.13.




5.14.
 ,
, ,
,

5.15.




5.16.




5.17.




5.18.
 ,
,
 ;
;
5.19.




5.20.




5.21.




5.22.




5.23.




5.24.




5.25.




5.26.




5.27.




5.28.




5.29.




5.30.




6.1-30. Даны вершины треугольника
 .Требуется
найти:
.Требуется
найти:а) длину стороны
 ;
б) уравнение
стороны
;
б) уравнение
стороны
 ;
;в) уравнение медианы
 ,проведённой
из вершины
,проведённой
из вершины
 ;
;г) уравнение высоты
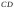 ,
проведённой из вершины
,
проведённой из вершины
 ;
;д) длину
 высоты
высоты
 ;
е)площадь
;
е)площадь
 треугольника
треугольника
 .Сделать
чертёж.
.Сделать
чертёж.6.1.
 .
6.2.
.
6.2.
6.3.
 6.4.
6.4.
6.5.
 6.6.
6.6.
6.7.
 6.8.
6.8.
6.9.
 6.10.
6.10.
6.11.
 6.12.
6.12.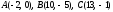
6.13.
 6.14.
6.14.
6.15.
 6.16.
6.16.
6.17.
 6.18.
6.18.
6.19.
 6.20.
6.20.
6.21.
 6.22.
6.22.
6.23.
 6.24.
6.24.
6.25.
 6.26.
6.26.
6.27.
 6.28.
6.28.
6.29.
 6.30.
6.30.
7.1 – 30. Даны вершины пирамиды
 .Требуется
найти:
.Требуется
найти: а) длины ребер
 и
и ;
б) угол
между ребрами
;
б) угол
между ребрами
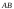 и
и ;
;
в) площадь грани
 ;
г)объем
пирамиды
;
г)объем
пирамиды
 ;
;д) уравнение плоскости грани
 ;
;е) длину
 высоты
высоты пирамиды
пирамиды
 .
.7.1.

7.2.

7.3.

7.4.

7.5.

7.6.

7.7.

7.8.

7.9.

7.10.

7.11.

7.12.

7.13.

7.14.

7.15.

7.16.

7.17.

7.18.

7.19.

7.20.

7.21.

7.22.

7.23.

7.24.

7.25.

7.26.

7.27.

7.28.

7.29.

7.30.

8.1–30. Установить, какую кривую определяет алгебраическое уравнение второго порядка, построить её.
8.1.
 8.2.
8.2.

8.3
 8.4
8.4
8.5.
 8.6.
8.6.
8.7.
 8.8.
8.8.

8.9.
 8.10.
8.10.

8.11
 8.12.
8.12.
8.13.
 8.14.
8.14.
8.15.
 8.16.
8.16.

8.17.
 8.18.
8.18.
 8.19.
8.19.
 8.20.
8.20. 8.21.
8.21. 8.22.
8.22. 8.23.
8.23. 8.24.
8.24. 8.25.
8.25. 8.26.
8.26.

8.27.
 8.28.
8.28.
8.29.
 8.30.
8.30.
9.1 – 30. Для указанной функции
 требуется
требуетсянайти область определения функции;
9.1. а)
 б)
б)

9.2. а)
 б)
б)
9.3. а)
 б)
б)
9.4. а)
 б)
б)
9.5. а)
 б)
б)
9.6. а)
 б)
б)
9.7. а)
 б)
б)
9.8. а)
 б)
б)
9.9. а)
 б)
б)
9.10. а)
 б)
б)
9.11 а)
 б)
б)
9.12 а)
 б)
б)
9.13 а)
 б)
б)
9.14 а)
 б)
б)
9.15 а)
 б)
б)
9.16 а)
 б)
б)
9.17 а)
 б)
б)
9.18 а)
 б)
б)
9.19 а)
 б)
б)
9.20 а)
 б)
б)
9.21 а)
 б)
б)
9.22 а)
 б)
б)
9.23 а)
 б)
б)
9.24 а)
 б)
б)
9.25 а)
 б)
б)
9.26 а)
 б)
б)
9.27 а)
 б)
б)
9.28 а)
 б)
б)
9.29 а)
 б)
б)
9.30 а)
 б)
б)
10.1-30. Вычислить пределы (не пользуясь правилом Лопиталя):
10.1. а)
 б)
б) в)
в)

г)

10.2. а)
 б)
б)
 в)
в)
г)

10.3. а)
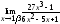 б)
б)
 в)
в)

г)

10.4. а)
 б)
б)
 в)
в)
г)

10.5. а)
 б)
б) в)
в)

г)

10.6. а)
 б)
б) в)
в)
г)

10.7. а)
 б)
б) в)
в)

г)

10.8 а)
 б)
б) в)
в)
г)

10.9. а)
 б)
б) в)
в)
г)

10.10. а)
 б)
б) в)
в)

г)

10.11. а)
 б)
б) в)
в)
г)

10.12. а)
 б)
б)
 в)
в)
г)

10.13. а)
 б)
б) в)
в)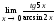
г)

10.14. а)
 б)
б) в)
в)
г)

10.15. а)
 б)
б) в)
в)
г)

10.16. а)
 б)
б) в)
в)
г)

10.17. а)
 б)
б) в)
в)
г)

10.18. а)
 б)
б) в)
в)
г)

10.19. а)
 б)
б) в)
в)
г)

10.20. а)
 б)
б) в)
в)
г)

10.21. а)
 б)
б) в)
в)
г)

10.22. а)
 б)
б) в)
в)
г)

10.23. а)
 б)
б) в)
в)
г)

10.24. а)
 б)
б) в)
в)
г)

10.25. а)
 б)
б) в)
в)

г)

10.26. а)
 б)
б) в)
в)

г)

10.27. а)
 б)
б) в)
в)

г)

10.28. а)
 б)
б) в)
в)

г)

10.29. а)
 б)
б) в)
в)
г)

10.30. а)
 б)
б)
 в)
в)
г)

11.1-30. Для указанной функции
 требуется:
а) выяснить
при каких значениях параметра
требуется:
а) выяснить
при каких значениях параметра
 функция
будет
непрерывной;
б) найти
точки разрыва
функции и исследовать их характер.
Построить
график функции.
функция
будет
непрерывной;
б) найти
точки разрыва
функции и исследовать их характер.
Построить
график функции.
1.1. а)
 б)
б)
11.2. а)
 б)
б)
113. а)
 б)
б)
11.4. а)
 б)
б)

11.5. а)
 б)
б)
11.6. а)
 б)
б)
11.7. а)
 б)
б)
11.8. а)
 б)
б)
11.9. а)
 б)
б)
11.10. а)
 б)
б)
11.11 а)
 б)
б)
11.12 а)
 б)
б)
11.13 а)
 б)
б)
11.14 а)
 б)
б)
11.15 а)
 б)
б)
11.16 а)
 б)
б)
11.17 а)
 б)
б)
11.18 а)
 б)
б)
11.19 а)
 б)
б)
11.20 а)
 б)
б)
11.21 а)
 б)
б)
11.22 а)
 б)
б)
11.23 а)
 б)
б)
11.24 а)
 б)
б)
11.25 а)
 б)
б)
11.26 а)
 б)
б)
11.27 а)
 б)
б)
11.28 а)
 б)
б)
11.29 а)
 б)
б)
11.30 а)
 б)
б)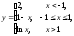
12.1-30. Даны комплексные числа
 ,
, ,
, и алгебраическое уравнение
и алгебраическое уравнение .
Требуется:а)
вычислить
.
Требуется:а)
вычислить
 ,
, ,
, ;
б)представить
комплексное число
;
б)представить
комплексное число
 в тригонометрической форме, вычислить
в тригонометрической форме, вычислить и результат представить в алгебраической
форме;в)
найти все
корни алгебраического уравнения на
множестве комплексных чисел.
и результат представить в алгебраической
форме;в)
найти все
корни алгебраического уравнения на
множестве комплексных чисел. 12.1.


 ;
;
12.2.


 ;
;
12.3.


 ;
;
12.4.


 ;
;
12.5.


 ;
; 12.6.
12.6.

 ;
;
12.7.


 ;
; 12.8.
12.8.

 ;
;
12.9.


 ;
;
12.10.


 ;
;
12.11.


 ;
; 12.12.
12.12.

 ;
;
12.13.


 ;
; 12.14.
12.14.

 ;
;
12.15.


 ;
; 12.16.
12.16.

 ;
;
12.17.


 ;
; 12.18.
12.18.

 ;
;
12.19.


 ;
; 12.20.
12.20.

 ;
;
12.21.


 ;
;
12.22.


 ;
;
12.23.


 ;
;
12.24.


 ;
;
12.25.


 ;
; 12.26.
12.26.

 ;
;
12.27.


 ;
;
12.28.


 ;
;
12.29.


 ;
;
12.30.


 ;
;
5.2. Вопросы к экзамену.
Раздел I. Линейная алгебра.
Понятие матрицы. Частные виды матриц (квадратная, треугольная, диагональная, нулевая, единичная). Элементарные преобразования матриц. Понятие эквивалентности и равенства матриц.
Действия над матрицами (сложение, вычитание, умножение матрицы на число, умножение матрицы на матрицу) и их свойства. Линейная комбинация матриц.
Определители 2-ого и 3-его порядка, их вычисление. Основные свойства определителей.
Понятие определителя n-ого порядка. Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя по элементам строки или столбца.
Понятие системы линейных уравнений (СЛУ). Частные виды СЛУ (квадратная, однородная, неоднородная). Матрица, расширенная матрица, определитель СЛУ.
Решение, множество решений СЛУ. Совместность, несовместность, определённость, неопределённость, эквивалентность СЛУ. Элементарные преобразования СЛУ, их основное свойство.
Формулы Крамера для решения СЛУ, условия их применимости.
Минор
 -ого
порядка, базисный минор, ранг матрицы.
Вычисление ранга матрицы. Критерий
совместности СЛУ (теорема Кронеккера-Капелли).
-ого
порядка, базисный минор, ранг матрицы.
Вычисление ранга матрицы. Критерий
совместности СЛУ (теорема Кронеккера-Капелли).Метод Гаусса решения СЛУ, условия его применимости. Условия несовместности, определённости и неопределённости СЛУ по методу Гаусса.
Преобразования СЛУ, выполняемые при выполнении прямого и обратного ходов метода Гаусса. Базисные и свободные переменные. Нахождение общего решения СЛУ.
Понятие обратной матрицы. Вырожденные и невырожденные матрицы. Теорема о существовании обратной матрицы. Основные способы нахождения обратной матрицы.
Матричные уравнения и их решение. Матричная форма записи СЛУ. Матричный способ (метод обратной матрицы) решения СЛУ и условия его применимости.
Однородные СЛУ, условия существования их ненулевых решений.
