§5.2. Конечные разности. Обобщенная степень.

Пусть задана функция . Обозначим черезфиксированную величину приращения аргумента (шаг). Тогда выражение

(5.3)

называется первой конечной разностью функции . Аналогично определяются конечные разности высших порядков

Например:

(5.4)

Символ (дельта) можно рассматривать как оператор, ставящий в соответствие функциифункцию.

Легко проверить основные свойства оператора :

1) ;

2) ;

3) , где(целые неотрицательные числа), причем.

Из формулы (5.3) имеем:

.

Отсюда, рассматривая как символический множитель, получим:

. (5.5)

Из формулы (5.4):

; (5.6)

и т.д. Окончательно получим:

. (5.7)

В дальнейшем нам понадобится понятие обобщенной степени.

Определение.

Обобщенной -степенью числаназывается произведениесомножителей, первый из которых равен, а каждый следующий наменьше предыдущего:

, (5.8)

где . Полагают, что. Приобобщенная степень совпадает с обычной:.

Вычислим конечные разности для обобщенной степени, полагая . Для первой конечной разности имеем:

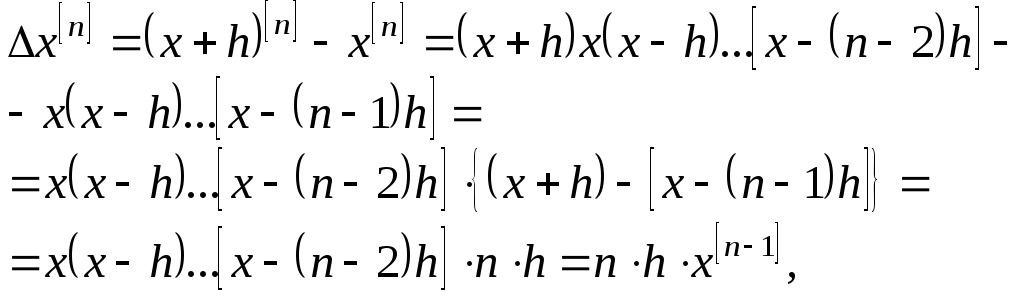
то есть

. (5.9)

Для второй конечной разности:

,

то есть

. (5.10)

Аналогично,

,

и так далее.

Окончательно будем иметь:

, (5.11)

, если . (5.12)

§5.3. Первая интерполяционная формула Ньютона.

Пусть для функции заданы значениядля равноотстоящих значений независимой переменной, где- шаг интерполяции. Требуется подобрать полиномстепени не выше, принимающий в точкахзначения

. (5.13)

Условия (5.13) эквивалентны тому, что

. (5.14)

Будем искать полином в виде

. (5.15)

Используя понятие обобщенной степени, запишем выражение (5.15) в виде:

. (5.16)

Чтобы полином был определен, нужно найти коэффициенты . Полагаяв выражении (5.16), получим

. (5.17)

Чтобы найти коэффициент , составим первую конечную разность:

.

Полагая , получим:

,

откуда

. (5.18)

Для определения коэффициента составим вторую конечную разность:

.

Положив , получим:

,

откуда

. (5.19)

Продолжая процесс, получим:

, (5.20)

причем .

Подставляя найденные значения коэффициентов в выражение (5.16), получим интерполяционный полином Ньютона:

. (5.21)

Этот полином полностью удовлетворяет требованиям поставленной задачи. Действительно, степень полинома не выше;;

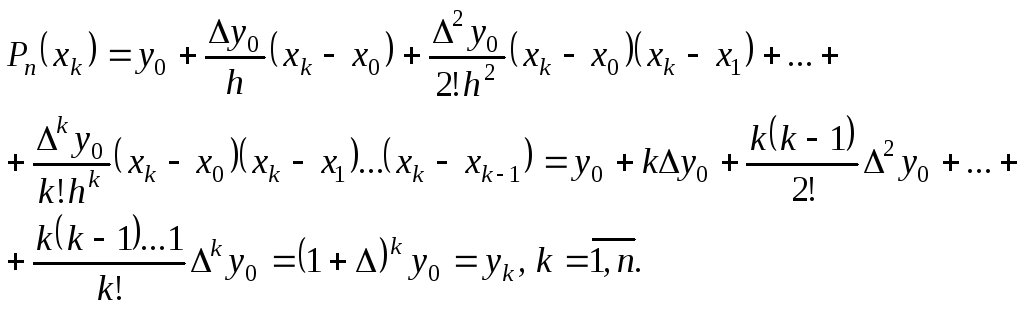
Для практического использования первую интерполяционную формулу Ньютона записывают в несколько преобразованном виде. Для этого введем новую переменную

. (5.22)

Тогда

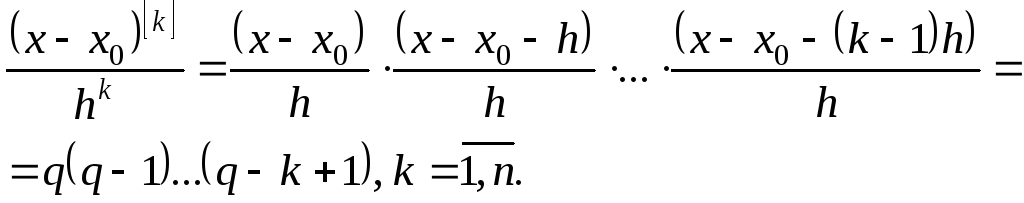(5.23)

Подставляя (5.23) в (5.21), получим окончательный вид первой интерполяционной формулы Ньютона:

. (5.24)

Если в формуле (5.24) положить , то получим формулу линейного интерполирования:

. (5.25)

При получим формулу параболического или квадратичного интерполирования:

. (5.26)

Первую интерполяционную формулу Ньютона используют для интерполирования функции в окрестности начальной точки , гдемало по абсолютной величине и представляет собой число шагов, необходимых для достижения точки, исходя из точки.

Остаточный член первой интерполяционной формулы Ньютона:

, (5.27)

где - некоторое промежуточное значение между узлами интерполированияи рассматриваемой точкой.

Учитывая, что 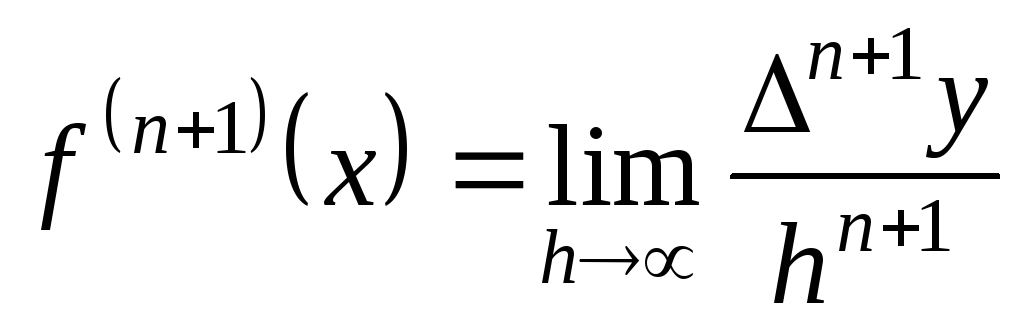, приближенно можно положить:

.

В этом случае соотношение (5.27) примет вид:

. (5.28)