§7.3. Квадратурная формула Гаусса.

Для вывода квадратурной формулы Гаусса потребуются некоторые сведения о полиномах Лежандра.

Определение 7.2.

Полиномы вида

называются полиномами Лежандра.

Полиномы Лежандра обладают следующими свойствами:

1) ;

2) , где- любой полином степени, меньшей;

3) полином Лежандра имеетразличных и действительных корней, которые расположены на интервале.

Свойство 2 называется свойством ортогональности полиномов Лежандра.

Перейдем к выводу квадратурной формулы Гаусса.

Рассмотрим сначала функцию , заданную на отрезке.

Поставим задачу: как нужно подобрать точки и коэффициенты, чтобы квадратурная формула

(7.15)

была точной для всех полиномов наивысшей возможной степени.

Так как в распоряжении имеется постоянныхи, а полином степениопределяетсякоэффициентами, то эта наивысшая степень в общем случае равна.

Для обеспечения равенства (7.15) необходимо и достаточно, чтобы оно было верным при .

Действительно, полагая

(7.16)

и

,

будем иметь:

.

Таким образом, учитывая соотношения:

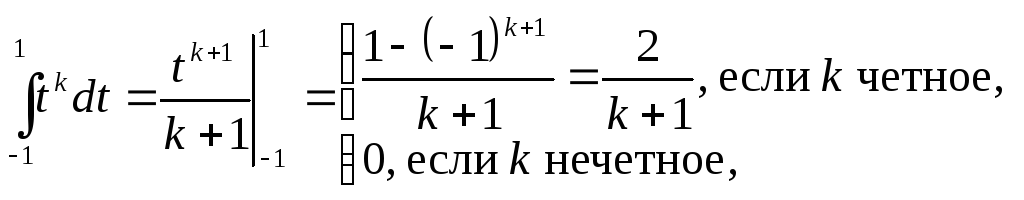
заключаем, что для решения поставленной задачи достаточно определить ииз системыуравнений

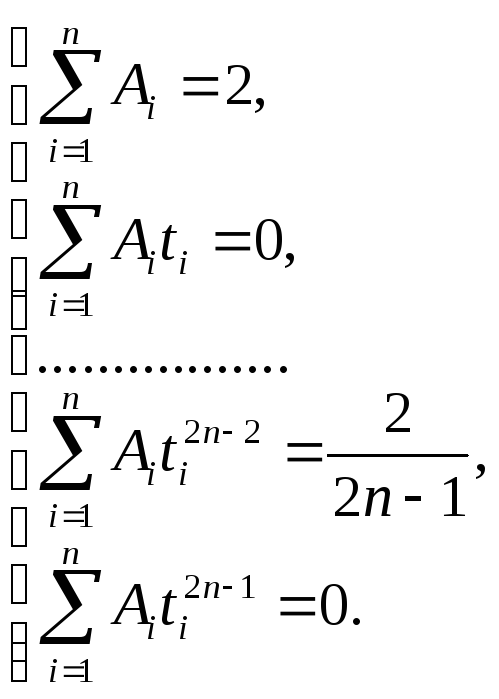(7.17)

Система (7.17) – нелинейная система, состоящая из уравнений снеизвестнымии. Решение ее обычным путем представляет большие математические трудности. Поэтому применяют искусственный прием.

Рассмотрим полином

,

где - полином Лежандра.

Так как степени этих полиномов не превышают , то на основании системы (7.17) для них должна быть справедлива формула (7.15):

. (7.18)

С другой стороны, в силу свойства ортогональности полиномов Лежандра выполнены равенства:

, при ,

поэтому в силу (7.18)

(7.19)

Если положить , то соотношения (7.19) будут выполняться при любых значениях.

Таким образом, для достижения наивысшей точности квадратурной формулы (7.15) в качестве точек достаточно взять нули соответствующего полинома Лежандра. В силу свойства 3 эти нули действительны, различны и расположены на интервале. Подставив найденные значенияв систему (7.17), которая при этом становится линейной, из первыхуравнений можно найти коэффициенты.

Определитель этой подсистемы является определителем Вандермонда

,

и, следовательно, коэффициенты определяются однозначно.

Формула (7.15), где - нули полинома Лежандраиопределяются из системы (3), называется квадратурной формулой Гаусса.

Неудобство применения квадратурной формулы Гаусса состоит в том, что абсциссы точек и коэффициенты- вообще говоря, иррациональные числа. Этот недостаток отчасти искупается ее высокой точностью при сравнительно малом числе ординат.

Для вычисления общего интеграла по квадратурной формуле Гаусса делают замену

.

Тогда

, (7.20)

где - нули полинома Лежандра,.

Соотношение (7.20) – квадратурная формула Гаусса для вычисления произвольного интеграла.

Остаточный член квадратурной формулы Гаусса (7.20) с узлами выражается следующим образом:

. (7.21)

§7.4. Приближенное вычисление несобственных интегралов.

Определение 7.3.

Интеграл

(7.22)

называется собственным, если

1. промежуток интегрирования 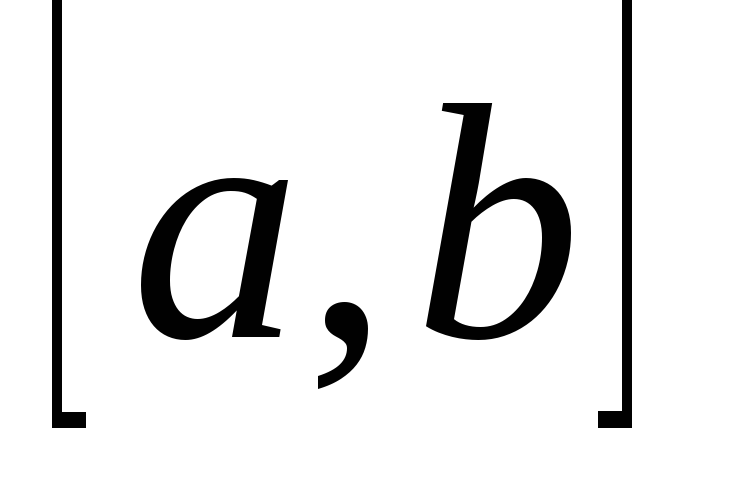конечен;

2. подынтегральная функция 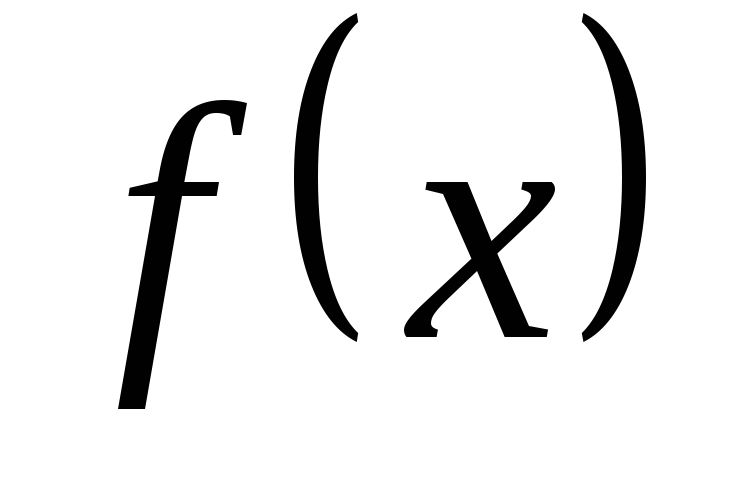непрерывна на.

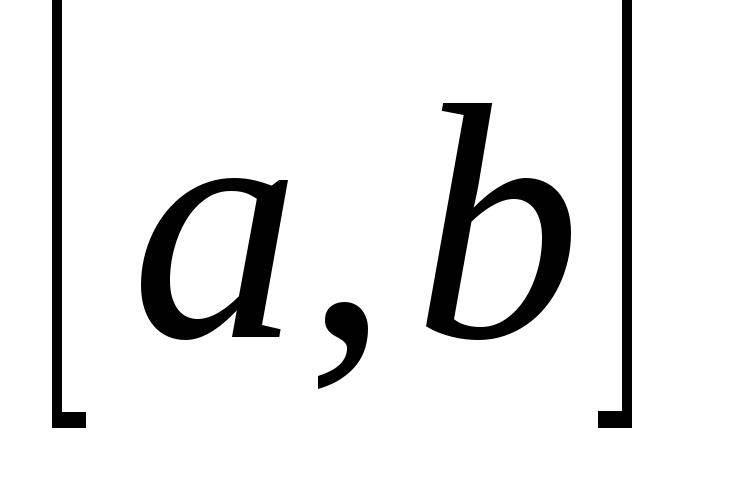В противном случае, интеграл (7.22) называется несобственным.

а). Рассмотрим приближенное вычисление несобственного интеграла

(7.23)

с бесконечным промежутком интегрирования, где функция непрерывна при.

Определение 7.4.

Интеграл (7.23) называется сходящимся (Рис.7.3), если существует конечный предел

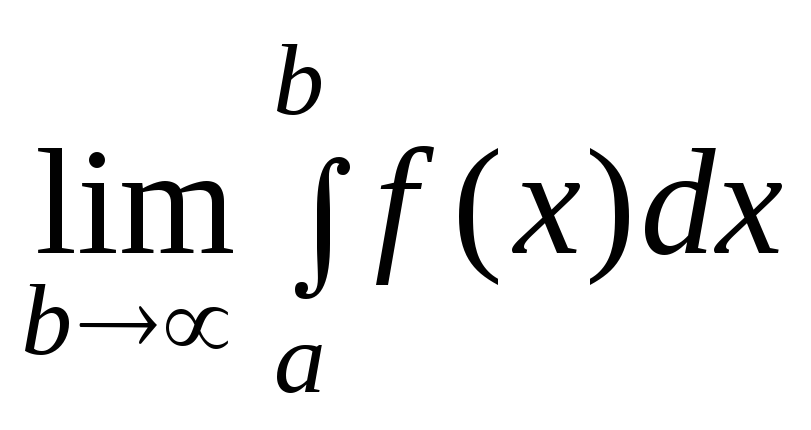(7.24)

и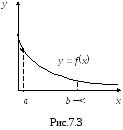по определению полагают

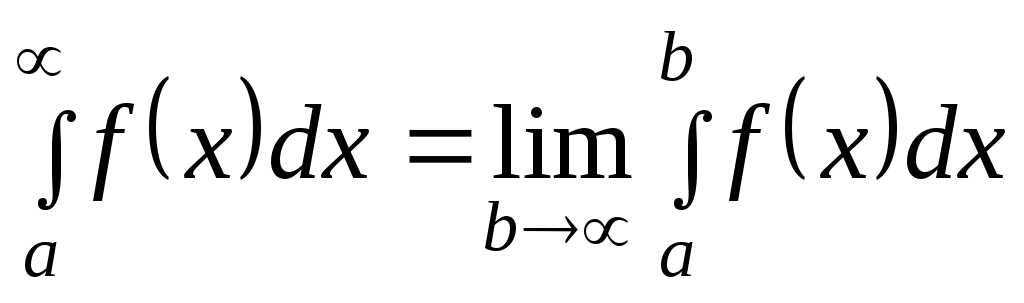(7.25)

Если предел (7.24) не существует, то интеграл (7.23) называется расходящимся, и такой интеграл считается лишенным смысла. Поэтому, прежде чем приступить к вычислению несобственного интеграла, нужно предварительно убедиться, что этот интеграл сходится.

Чтобы вычислить сходящийся несобственный интеграл (7.23) с заданной точностью , представим его в виде

(7.26)

В силу сходимости интеграла число можно выбрать столь большим, чтобы имело место неравенство

(7.27)

Собственный интеграл можно вычислить по одной из квадратурных формул. Пусть- приближенное значение этого интеграла с точностью до, т.е.

. (7.28)

Из формул (7.26)-(7.28) имеем

,

т.е. поставленная задача решена.

б). Допустим теперь, что отрезок конечен, а функцияимеет конечное число точек разрыва на. Эти точки назовем «особыми» и обозначим. Такими особыми точками могут быть или один из концов отрезка, или оба конца отрезка, либо одна или несколько точек внутри отрезка.

Так как промежуток интегрирования можно разбить на частичные промежутки с единственной точкой разрыва подынтегральной функции, то достаточно разобрать лишь случай, когда на имеется единственная точка разрывафункции, причем второго рода.

Если есть внутренняя точка отрезка, то по определению полагают:

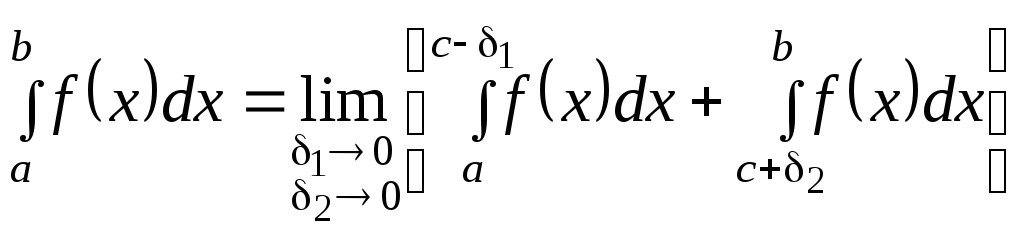, (7.29)

и в случае существования этого предела интеграл называют сходящимся, в противном случае – расходящимся.

Аналогично определяется сходимость несобственного интеграла, если точка разрыва подынтегральной функциисовпадает с одним из концов промежутка интегрирования.

Для приближенного вычисления с заданной точностью сходящегося несобственного интеграла (7.29), где точка разрыва, выбирают положительные числаистоль малыми, чтобы имело место неравенство:

.

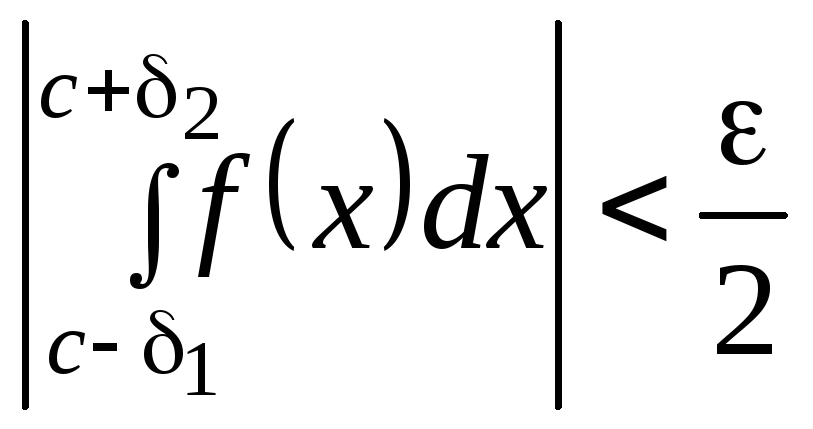Затем по известным квадратурным формулам вычисляют определенные интегралы 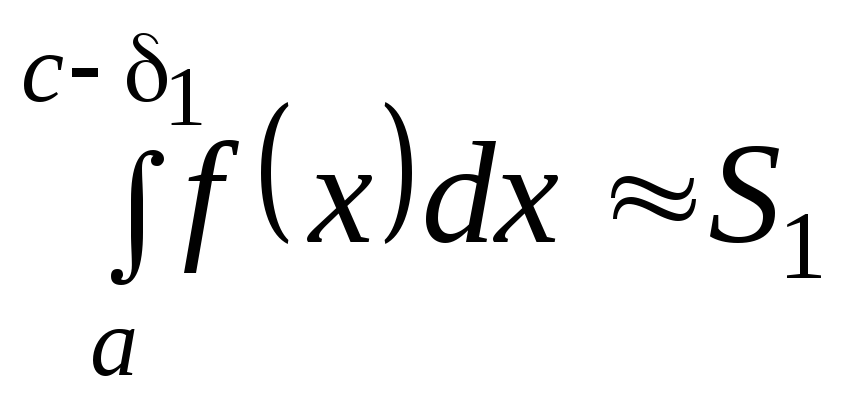,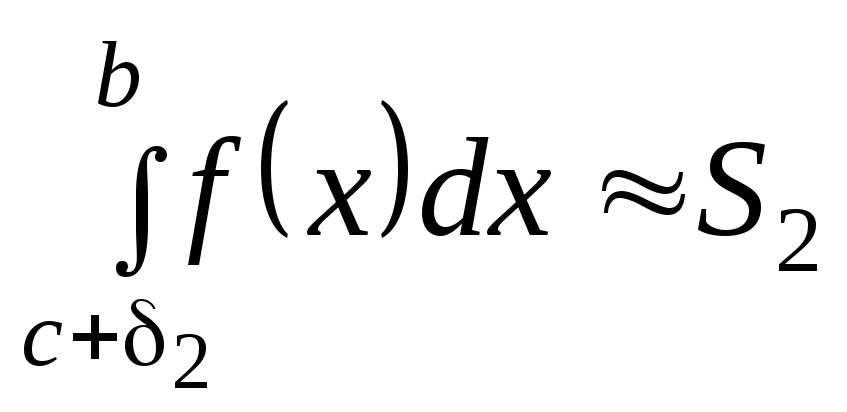с точностью до. Тогдас точностью, т.е.

.

Если точка разрыва подынтегральной функцииявляется концевой для промежутка интегрирования, то методика вычисления очевидным образом видоизменяется.