6.5. Индуктивная катушка в цепи синусоидального тока

     Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции

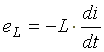(6.9)

     Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = e_L = 0.

(6.10)

     Таким образом, ток в индуктивности отстает по фазе от напряжения на 90^o из-за явления самоиндукции.      Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:

(6.11)

     Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0^o< φ < 90^o), величина которого зависит от соотношения R и L.      Выражение (6.11) в комплексной форме записи имеет вид:

(6.12)

      где Z_L - полное комплексное сопротивление индуктивной катушки ;             Z_L - модуль комплексного сопротивления;            - начальная фаза комплексного сопротивления;- индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).       Полное сопротивление индуктивной катушки или модуль комплексного сопротивления

.

       Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.6.5).

Рис. 6.5

       Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90^o.     В цепи  переменного тока напряжения на  участках цепи складываются не арифметически, а геометрически.        Если мы поделим стороны треугольника напряжений на величину тока I_m, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).

 

Рис. 6.6

 Из треугольника сопротивлений получим несколько формул:                      ;;

;

;           .

6.6. Емкость в цепи синусоидального тока

     Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток

;

.    (6.13)

      Из анализа выражений 6.13 следует, что ток опережает напряжение по фазе на 90^o.

      Выражение (6.13) в комплексной форме записи имеет вид:

,    (6.14)

       где - емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления.

        Если комплексное сопротивление индуктивности положительно        , то комплексное сопротивление емкости отрицательно.

       На рис. 6.7 изображена векторная диаграмма цепи с емкостью.        Вектор тока опережает вектор напряжения на 90^o.

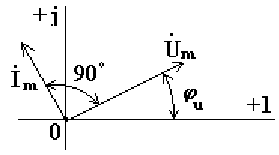Рис. 6.7

6.10. Мощность в цепи синусоидального тока

     Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток.      Пусть мгновенные напряжение и ток определяются по формулам:

     Тогда

     (6.23)

     Среднее значение мгновенной мощности за период

     Из треугольника сопротивлений ,      а.

     Получим еще одну формулу:

.

     Среднее арифметическое значение мощности за период называют активной мощностью и обозначают буквой P.    Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии, например, в тепловую, световую и механическую энергию.      Возьмем реактивный элемент (индуктивность или емкость). Активная мощность в этом элементе , так как напряжение и ток в индуктивности или емкости различаются по фазе на 90^o. В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов.    Происходит обратимый  процесс в  виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.      Преобразуем выражение (6.23):

     где - мгновенная мощность в активном сопротивлении;

      - мгновенная мощность в реактивном элементе (в индуктивности или в емкости).    Максимальное или амплитудное значение мощности p₂ называется реактивной мощностью

,

     где x - реактивное сопротивление (индуктивное или емкостное).      Реактивная мощность, измеряемая в вольтамперах реактивных, расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.      Амплитудное значение суммарной мощности p = p₁ + p₂ называется полной мощностью.    Полная  мощность,  измеряемая в вольтамперах, равна произведению действующих значений напряжения и тока:

,

     где z - полное сопротивление цепи.    Полная мощность характеризует предельные возможности источника энергии. В электрической цепи можно использовать часть полной мощности

,

       где   - коэффициент мощности или "косинус "фи".

  Коэффициент  мощности  является одной из важнейших характеристик электротехнических устройств. Принимают специальные меры к увеличению коэффициента мощности.       Возьмем треугольник сопротивлений и умножим его стороны на квадрат тока в цепи. Получим подобный треугольник мощностей (рис. 6.18).

     Из треугольника мощностей получим ряд формул:

,      ,

             Рис.6.18                                                                 ,.      При анализе электрических цепей символическим методом используют выражение комплексной мощности, равное произведению комплексного напряжения на сопряженный комплекс тока.      Для цепи, имеющей индуктивный характер (R-L цепи)

,

       где         - комплекс напряжения;- комплекс тока;- сопряженный комплекс тока;- сдвиг по фазе между напряжением и током., ток как в R-L цепи, напряжение опережает по фазе ток.

     Вещественной частью полной комплексной мощности является активная мощность.      Мнимой частью комплексной мощности - реактивная мощность.      Для цепи, имеющей емкостной характер (R-С цепи), . Ток опережает по фазе напряжение.

.

     Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, - положительна, а в цепи с емкостным характером - отрицательна.