Пьезорезонансные преобразователи

В пьезоэлектрическом резонаторе происходит преобразование электрического напряжения между электродами в деформацию и механические напряжения в пьезоэлементе, которые вызывают ответ­ную реакцию по выходу в виде зарядов на электродах, возникающих под действием механических напряжений. Обратимость пьезоэлектри­ческого эффекта позволяет выполнять пьезорезонатор в виде двухполюсника, объединяющего системы электрического возбуждения механических колебаний и съема электрического сигнала. Резонанс­ные колебания в пьезоэлементе возникают в результате установления в нем стоячих ультразвуковых волн. Длина волны

 = lf,

где  – скорость распространения ультразвука; f – частота излучения.

Ско­рость распространения ультразвука в материале определяется формулой:

=,

где Е_ij – константа упругости;  – плотность материала. Следовательно, длина волны

.

Если длина волны  такова, что на отрезке h между гранями, от которых отражаются волны, укладывается целое число полуволн, то в пьезоэлементе устанавливаются стоячие волны. Таким образом, сто­ячим волнам соответствует частота возбуждающего напряжения

,

где n – число уложившихся полуволн.

Частота колебаний, при которых на длине h укладывается одна полуволна, является основной частотой и равна

.

При частотах, которые значи­тельно меньше f_К, ток в цепи возбуждающих электродов (рис. 2-19, а) мал и определяется в основном межэлектродной емкостью С₀ и сопротивлением изоляции между электродами R₀.

По мере приближения частоты возбуждающего напряжения к ча­стоте f_R амплитуда механических колебаний растет. Пропорционально амплитуде колебаний увеличивается заряд на электродах, и в цепи воз­растает составляющая переменного тока, вызываемая деформациями пьезоэлемента.

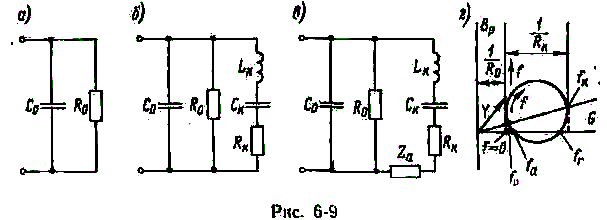
Рис. 2-19

На рис. 2-19, б представлена эквивалентная схема пьезорезонатора. В этой схеме введены эквивалентные параметры: индук­тивность L_K = mIk²_эм, емкость С_К = nk²_эм и сопротивление R_К, образу­ющие динамический контур эквивалентной схемы. Схема рис. 2-19, б соответствует свободно колеблющемуся, т.е. механически не нагру­женному, пьезорезонатору (режим короткого замыкания, при котором усилия на поверхностях пьезоэлемента от внешних сил равны нулю). Схема рис. 2-19, в учитывает влияние внешних нагрузок в виде вклю­ченного сопротивления Z_a, которое может иметь как чисто активный (например, если существуют потери на акустическое излучение во внешнюю среду), так и реактивный (например, при присоединении к пьезоэлементу дополнительной массы) характер. В заторможен­ном состоянии, когда скорости смещений поверхностей пьезоэлемента равны нулю, сопротивление Z_a равно бесконечности (режим холостого хода). В режиме, близком к холостому ходу, работают пьезоэлектрические датчики давлений и ускорений, в которых используется прямой пьезоэффект. Поэтому в эквивалентной схеме этих датчиков динамиче­ская ветвь обычно не учитывается.

Проводимость эквивалентной схемы (рис. 2-19, б) определяется как

.

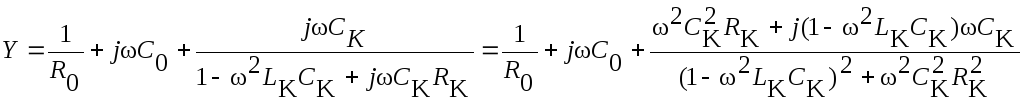Для идеального пьезорезонатора (R₀ = , R_К = 0) проводимость бесконечно возрастает при условии 1 – ²L_KC_K = 0, т.е. при частоте _R = , называемой частотой последовательного резонанса. Эта частота определяется исключительно параметрами введенного ди­намического контура и поэтому совпадает с определенной ранее как – частотой механического резонанса.

Проводимость идеального пьезорезонатора бесконечно падает при условии jC₀+, при частоте , называемой частотой параллельного резонанса (а иногда частотой антирезонанса).

Относительная разность между частотами последовательного и параллельного резонансов составляет (_Р – _К)/_К = С_К/(2С₀). Для пьезорезонаторов из кварца емкостное отношение не превышает С_К/С₀ = 10^-2 – 10^-3 и частота _Р может быть выше частоты _К не более чем на 0,5%. Соответственно и изменение частоты параллельного резо­нанса путем подключения параллельно резонатору добавочной емко­сти С'₀ и увеличения таким образом емкости С₀ возможно не более чем на 0,1 – 0,01%.

В реальном пьезорезонаторе при частотах _К и _Р проводимости контура не равны бесконечности и нулю, они имеют некоторое конечное значение, включающее в себя, кроме активной, и небольшую реактивную составляющую. Поэтому для характеристики пьезорезонатора вводятся еще две частоты, при которых проводимость чисто активная. Одна из этих частот _r называется частотой резо­нанса и оказывается чуть больше частоты _K, вторая (_a) называется ча­стотой антирезонанса и оказывается чуть ниже частоты _P. Вектор­ная диаграмма проводимости контура с указанием характерных точек показана на рис. 2-19, г.

Важной характеристикой контура является его добротность

Q = _KL_K/R_K,

определяемая потерями энергии при колебаниях. В со­став потерь входят: потери собственно в кварце, потери в материалах электродов, потери на акустическое излучение в окружающую среду, потери на границе колеблющегося элемента и неподвижных элемен­тов крепления, потери во входном элементе присоединяемой электри­ческой схемы. Теоретическая добротность кварцевых резонаторов, если учитывать только потери в кварце, может достигать значения, определяемого из соотношения Qf_r = 1,2·10¹³, реальные добротности зависят от конструкции резонаторов[1].

Основой пьезорезонансного частотного датчика является пьезорезонатор, частота которого изменяется под действием измеряемой величины. Изменение частоты может происходить:

а) при воздей­ствии температуры, которая влияет на геометрические размеры, плотность и, главным образом, на упругие свойства кварца;

б) под дей­ствием механических напряжений в резонаторе или его деформации, также вызывающих изменение h,  и n;

в) при присоединении допол­нительной массы к резонатору, изменяющей его толщину h и сред­нюю плотность .

Соответственно различают термочувствительные, тензочувствительные и массочувствительные пьезорезонаторы. Кроме этого, используются пьезорезонансные датчики с амплитудным выхо­дом. В этих датчиках, работающих на частоте, близкой к резонансной, при изменении акустических потерь меняется амплитуда колеба­ний.

При построении пьезорезонансного датчика очевидны требования, предъявляемые к пьезорезонатору: высокая добротность, высокая чувствительность к измеряемой величине, малая чувствительность к дестабилизирующим факторам и возможность возбуждения колеба­ний только на одной частоте, т.е. моночастотность. Эти требования обеспечиваются, в первую очередь, выбором типа среза пьезоэлемента и типа возбуждаемых в пьезоэлементе колебаний. Действительно, если рассмотрим пластину Y-среза, то при приложении поля в направ­лении оси Y в ней возникают деформа­ции ₅ и ₆, деформирующие пьезоэлемент в плоскости хz (деформация сдвига вдоль грани) и в плоскости ху (деформация сдвига по толщине). Однако геометрические размеры, определяющие резонансную частоту, в этих случаях различны. Собственная частота колебаний сдвига вдоль грани значительно ниже частоты колебаний сдвига по толщине, и бла­годаря этому условие моночастотности соблюдается удовлетворительно. В управляемых пьезорезонаторах чаще всего используются именно колебания сдвига по толщине (хотя возможны и другие типы колебаний), так как при этом типе колебаний колебательная энергия концентриру­ется в подэлектродной области пьезоэлемента. Безэлектродные перифе­рийные области оказываются практически свободными от упругих коле­баний, что позволяет осуществлять крепление пьезоэлемента без замет­ного ухудшения добротностей. Ослабление амплитуды колебаний при ′h′/(h)=0,02 (' и h' – плотность и толщина электрода,  и h – плот­ность и толщина пьезоэлемента) в точке, удаленной от края электрода на 15 h, составляет не менее 40 дБ. При применении линзового резонатора эффект локализации энергии может быть ещё больше.