6. Способы преобразования комплексного чертежа

Рассматривая способы решения позиционных задач в предыдущих разделах, следует отметить, что задачи решаются значительно проще, если геометрические объекты (прямые или плоскости) занимают частные положения относительно плоскостей проекций. Особенно это важно при решении метрических задач (определение натуральных значений расстояний, длин, площадей, углов и т. п.).

Перевод геометрического объекта из общего положения в частное можно осуществить двумя путями:

1. изменением положения плоскостей проекций относительно геометрических объектов, которые остаются неподвижными;

2. перемещением геометрических объектов относительно плоскостей проекций, которые остаются неподвижными.

6.1. Способ введения новых плоскостей проекций

1. Новая плоскость проекций должны быть перпендикулярной к одной из имеющихся плоскостей проекций. Любую, перпендикулярную к ₁ или ₂ плоскость, можно принять за новую плоскость проекций ₃ или ₄ (рис.5.1,5.2).

Рис.6.1 Рис.6.2

Этим способом можно решить четыре основные задачи на преобразование комплексного чертежа:

1. преобразование прямой общего положения в прямую уровня;

2. преобразование прямой общего положения в проецирующую прямую;

3. преобразование плоскости общего положения в проецирующую плоскость;

4. преобразование плоскости общего положения в плоскость уровня.

Рассмотрим эти задачи на примерах.

Пример 1. Преобразовать прямую а общего положения в прямую уровня и затем в проецирующую прямую (рис.6.3).

Решение: Выберем на прямой а две точки А и В и введем новую плоскость проекций ₃, параллельную горизонтальной проекции этой прямой и перпендикулярно плоскости ₁, и спроецируем прямую а (А, В) ортогонально на эту плоскость. Получим новую проекцию а^”’(A^”’,B^’”) . Первая основная задача решена. Чтобы решить вторую основную задачу, продолжим построения дальше: Введем новую плоскость проекций ₄, перпендикулярную проекции а^”’(A^”’,B^’”). Эта плоскость пересечет ₃ по оси х₂. Спроецируем на новую плоскость нашу прямую а (А, В) в точку а^IV (A^IV, B^IV). Вторая основная задача решена. Она, как промежуточное построение, содержит первую основную задачу.

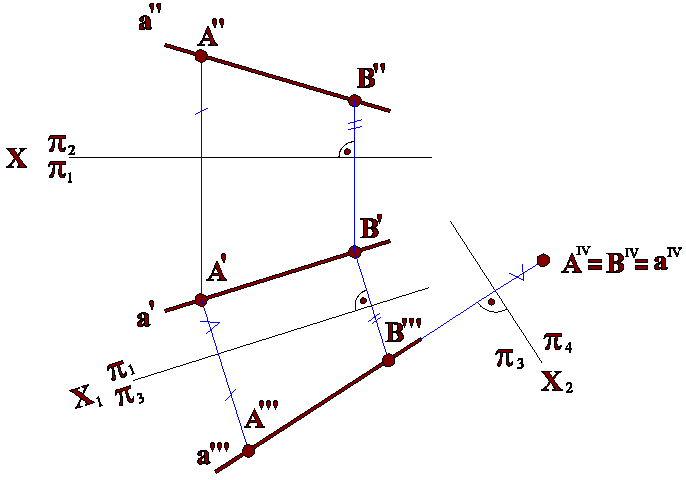
Рис. 6.3

Пример 2. Преобразовать плоскость общего положения (АВС) в проецирующую плоскость с последующим переводом ее в плоскость уровня рис. 6.4 (третья и четвертая основные задачи).

Рис.6.4

Решение: Проведем в плоскости треугольника АВС линию уровня, например, горизонталь h, и введем новую плоскость проекций ₃, перпендикулярную этой линии уровня, и спроецируем на нее треугольник АВС. Получим прямую (B^”’C^”’A^”’), в которую он выродится. Третья основная задача решена. Решаем четвертую основную задачу “преобразование проецирующей плоскости в плоскость уровня”. Параллельно прямой (B^”’C^”’A^”’) вводим новую плоскость проекций ₄ на которую заданный треугольник АВС будет проецироваться в натуральную величину. Четвертая основная задача решена.

6.2. Построение изображений фигур по заданному направлению

В машиностроительном черчении часто необходимо строить изображения заданных предметов или их частей по заданному направлению, указанному обычно стрелкой.

Пример 1. Построить изображение окружности по стрелке S.(рис.6.5).

Решение: Поскольку направление S параллельно фронтальной плоскости проекций, то новую плоскость проекций выбираем перпендикулярно направлению S`` и строим изображение этой фигуры на этой плоскости.

Рис.6.5

Пример 2. (рис.6.6). Построить изображение призмы по заданному направлению s общего положения в пространстве.

Решение: Перпендикулярно направлению s^” проводим ось проекций х₁, а перпендикулярно направлению s^’ - ось х₂. Построение нового изображения призмы показано на чертеже и дальнейших пояснений не требует.

Рис.6.6