
- •Курс лекций по
- •1. Понятие об операции проецирования
- •1.1. Основные свойства ортогонального поецирования
- •1.2. Эпюр гаспара монжа или комплексный чертеж
- •1.3 Безосный комплексный чертеж
- •2. Прямая. Проекции прямой линии
- •2.1. Прямые общего и частного положения
- •2.2. Определение натуральной величины и углов наклона отрезка прямой к плоскостям проекций.
- •2.4. Следы прямой линии
- •2.5. Взаимное положение двух прямых в пространстве
- •3. Плоскость. Задание плоскости на комплексном чертеже.
- •3.1 Плоскости общего и частного положений в пространстве.
- •3.2. Прямые и точки на плоскости. Главные линии на плоскости.
- •3.3. Линии наибольшего наклона плоскости к плоскостям проекций
- •4. Взаимное положение прямых и плоскостей.
- •4.1 Взаимная параллельность прямой и плоскости.
- •4.2 Взаимная параллельность двух плоскостей
- •4.3 Взаимное пересечение прямой и плоскости.
- •4.4 Взаимное пересечение двух плоскостей
- •4.5 Взаимное пересечение плоскостей, заданных следами.
- •5. Изображение многогранников
- •5.1 Виды многогранников
- •5.2 Пересечение прямой линии с поверхностью многогранника
- •5.3 Пересечение многогранника плоскостью общего положения
- •6. Способы преобразования комплексного чертежа
- •6.1. Способ введения новых плоскостей проекций
- •6.2. Построение изображений фигур по заданному направлению
- •6.3. Способы вращения вокруг прямых частного положения
- •6.3.1. Способ вращения вокруг проецирующих прямых
- •6.3.2. Способ вращения вокруг линии уровня
- •6.4. Cпособ плоскопараллельного перемещения
- •7. Взаимная перпендикулярность прямых и плоскостей
- •7.1. Взаимная перпендикулярность прямой и плоскости
- •Признак перпендикулярности прямой и плоскости на чертеже.
- •7.2. Взаимная перпендикулярность двух прямых общего положения в пространстве
- •7.3. Взаимная перпендикулярность двух плоскостей общего положения в пространстве
- •8. Метрические задачи и способы их решения
- •8.1. Решение метрических задач в общем виде
- •8.2. Решение метрических задач способами преобразования комплексного чертежа
- •8.3. Измерение расстояний
- •8.4. Измерение углов
- •9. Кривые линии и кривые поверхности
- •9.1. Кривые линии
- •9.2. Плоские кривые линии
- •9.3. Пространственные кривые
- •9.4. Проецирование кривых линий
- •9.5. Особые точки кривой линии
- •10. Поверхности
- •10.1. Способы образования и задания кривых поверхностей
- •10.2 Классификация поверхностей
- •10.3. Линейчатые поверхности
- •10.4. Поверхности вращения
- •10.5. Поверхности, задаваемые каркасом
- •10.6. Поверхности второго порядка
- •10.7. Некоторые свойства поверхностей второго порядка
- •10.8. Сечение поверхности проецирующей плоскостью и прямой линией
- •10.9 Конические сечения
- •10.10 Пересечение прямой с кривой поверхностью
- •10.11. Взаимное пересечение кривых поверхностей
- •1. Возможности применения способа вспомогательных секущих плоскостей в качестве “посредников”.
- •2. Возможности применения вспомогательных секущих сфер в качестве “посредников”.
- •10.12. Взаимное пересечение поверхностей второго порядка
- •10.13. Развертки кривых поверхностей
- •11. Аксонометрические проекции
- •11.1. Теоремы ортогональной аксонометрии
- •11.2. Стандартные аксонометрические проекции
- •Прямоугольная диметрическая проекция
- •11.3. Изображение окружности в координатной плоскости изометрической проекции
- •11.4. Изображение окружностей в координатных плоскостях диметрической проекции
- •11.5. Построение аксонометрических изображений простейших геометрических тел и задание точек на их поверхностях
- •12. Плоскости и прямые, касательные к кривым поверхностям
- •12.1. Проведение касательных к плоским кривым линиям.
- •12.2. Плоскости и прямые, касательные к кривой поверхности в данной точке
- •12.3. Примеры построения плоскостей, касательных к некоторым кривым поверхностям
- •12.4. Примеры построения прямых, касательных к кривым поверхностям в данной точке
- •12.5. Взаимное касание кривых поверхностей
- •12.6. Построение геометрических мест и их применение к решению задач
2.4. Следы прямой линии
“Следами” прямой линии называют точки пересечения прямой с плоскостями проекций.У прямой линии могут быть максимум три следа на основных плоскостях проекций.
Таким образом, прямая линия на чертеже, может быть задана ее следами.
Нахождение следов прямой линии показано на рис.(2.11;12).


Рис.2.11 Рис.2.12
2.5. Взаимное положение двух прямых в пространстве
Из стереометрии известно, что две прямые в пространстве могут быть параллельными, пересекающимися и скрещивающимися. (рис.2.13, 2.14, 2.15).



Рис. 2.13 Рис. 2.14 Рис. 2.15
Видимость двух скрещивающихся прямых (одна прямая на той или иной плоскости проекций может перекрывать другую прямую или быть перекрыта этой прямой). Для определения “видимости” линий в этом случае можно воспользоваться так называемыми “конкурирующими” точками, то есть точками, лежащими на одной проецирующей прямой. На рис.2.15 такими конкурирующими точками являются точки 1 и 2 и 3 и 4.
Литература: Гордон В.О. и др. Курс начертательной геометрии. §§10,11-14.; Фролов С.А. Начертательная геометрия. с. 34,-38.; Локтев В.О. Краткий курс начертательной геометрии. Гл.II.
3. Плоскость. Задание плоскости на комплексном чертеже.
Плоскость на комплексном чертеже можно задать:
тремя точками, не лежащими на одной прямой;
точкой и прямой, не проходящей через эту точку;
двумя параллельными прямыми;
двумя пересекающимися прямыми;
плоской фигурой;
следами.
Следами плоскости называются линии пересечения плоскости с плоскостями проекций.
Некоторые примеры задания плоскости.
Плоскость ( А, В, С) - заданная плоской фигурой (рис. 3.1). Плоскость (h0 f0) - заданная следами этой плоскости на плоскостях проекций - линиями h0 и f0 (рис.3.2а и 3.2б).



Рис. 3.1 Рис. 3.2а Рис. 3.2б
3.1 Плоскости общего и частного положений в пространстве.
В зависимости от положения плоскости относительно плоскостей проекций плоскость может занимать общее или частное положение.
Плоскости, не параллельные и не перпендикулярные ни к одной из плоскостей проекций, называются плоскостями общего положения в пространстве (рис.3.1 и рис.3.2а и 3.2б).
Плоскости, перпендикулярные к одной из плоскостей проекций, называются проецирующими плоскостями. Соответственно они называются: горизонтально проецирующими, фронтально проецирующими и профильно проецирующими плоскостями (рис.3.3а, 3.3б, 3.3с).
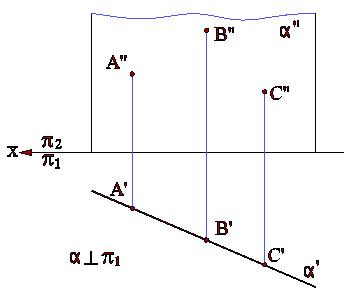


Рис. 3.3а Рис. 3.3б Рис. 3.3с
Плоскости, параллельные одной из плоскостей проекций, называются плоскостями уровня. Соответственно различают: горизонтальные, фронтальные и профильные плоскости уровня, (показаны на рис. 3.4а, 3.4б и 3.4с).



Рис. 3.4а Рис. 3.4б Рис. 3.4с
