3. Электропроводность полупроводников

Внешнее электрическое поле напряженностью E, приложенное к полупроводнику n-типа, вызывает направленное движение, дрейф электронов в направлении, противоположном полю. Поскольку плотность тока j есть заряд, проходящий в единицу времени через единичное сечение площадки, перпендикулярной направлению дрейфа электронов, то

j=qn_ov_др=qn_oµ_nE, (1.16)

где q – заряд электрона: v_др– скорость дрейфа электронов; µ_n– подвижность электронов, т.е. их дрейфовая скорость в поле единичной напряженности

µ_n=v_др/E.

Из сравнения (1.16) с законом Ома в дифференциальной форме j = σE следует, что проводимость σ полупроводника n-типа определяется соотношением

σ = qn_oµ_n(1.17).

Основными механизмами, определяющими подвижность электронов, является рассеяние на ионизированных атомах примеси и на тепловых колебаниях кристаллической решетки, которые нарушают их направленное движение и ограничивают значение µ_n. Сказанное справедливо и для дырок в случае полупроводника р-типа.

В области низких температур, когда колебания кристаллической решетки малы, основную роль играет рассеяние на ионизированных атомах примеси и µ~Т ^3/2. В области высоких температур преобладает рассеяние на тепловых колебаниях решетки, которое возрастает с повышением температуры, и µ~Т^-3/2.

Общий вид зависимости µ(Т), обусловленный комбинацией обоих типов рассеяния, показан на рис.1.3. Например, для Ge с концентрацией ионизированных атомов примеси ≈ 10¹⁷см^-3решетчатое рассеяние преобладает при T > 60 К.

В случае собственного полупроводника выражение для проводи-мости примет вид

σ_i = q(n₀µ_n + p₀µ_p) = q(µ_n + µ_p)n_i.

З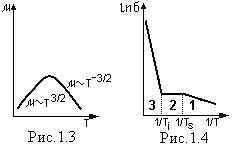ная температурные зависимости концентрации носителей заряда и их подвижности, можно определить зависимость проводимости полу-проводника от температуры.

В случае примесного полупроводника n-типа зависимость lnσ от 1/Т приведена на рис.1.4, где можно выделить три области: низких температур 1, истощения примеси 2 и собственной проводимости 3. В области низких температур согласно (1.12) и (1.17) имеем

, где.

Влияние температурной зависимости подвижности носителей сказывается мало в силу преобладающего фактора экспоненциального изменения концентрации носителей от температуры. Поэтому график представляет собой прямую, тангенс угла наклона которой равен ΔE_d/2k.

В области истощения примеси концентрация носителей заряда не изменяется, и характер зависимости lnσ от Т определяется температурной зависимостью подвижности носителей. Если в этой области преобладает рассеяние на тепловых колебаниях решетки, то проводимость на этом участке падает.

В области собственной проводимости график lnσ представляет собой прямую с угловым коэффициентом, равным ΔEg/2k.

Экспериментально снятые данные зависимости lnσ от Т позволяют определить ширину запрещенной зоны полупроводника, энергию ионизации примеси и характер рассеяния носителей заряда.

4. Эффект Холла

Эффектом Холла называется явление, состоящее в том, что при пропускании тока вдоль проводящей пластинки, помещенной перпендикулярно линиям внешнего магнитного поля, возникает поперечная разность потенциалов вследствие взаимодействия носителей заряда с магнитным полем.

Пусть имеется полупроводник n-типа, имеющий форму прямоугольной пластинки с размерами: длина а, ширинаb, толщинаd(рис..1.5). по пластинке в направлении оси Y протекает электрический ток плотности j = qn_ov_др, и электроны совершают дрейф в противоположном направлении. Если поместить пластинку в магнитное поле с индукцией B, направленной по оси Z, то на электроны, движущиеся со скоростью v_др, в магнитном поле будет действовать сила Лоренца

.

Так как угол между иравен 90⁰, то численное значение силы Лоренца составляет

F_л=qv_дрВ.

Она направлена, согласно правила буравчика и с учетом знака минус для электрона, по оси Х. Под действием силы Лоренца электроны будут отклоняться в направлении оси Х, заряжая боковую поверхность пластинки А отрицательно. На противоположной боковой поверхности С возникает дефицит электронов, что приведет к возникновению нескомпенсированного положительного заряда. Разделение зарядов приводит к возник-новению электрического поля, направленного от С к А и равного

E_к =V_H/b (1.18)

Где V_H– э.д.с. Холла – разность потенциалов между точками С и А. Напряженность поля E_к будет расти до тех пор, пока сила, обусловленная этим полем,не скомпенсирует силу Лоренца

qE _H=qv_дрB

Учитывая (1.18) и то, что плотность тока j=qn_ov_др, получим

V_H= -(1/qn_o)Bjb. (1.19)

Величина R_H= -

н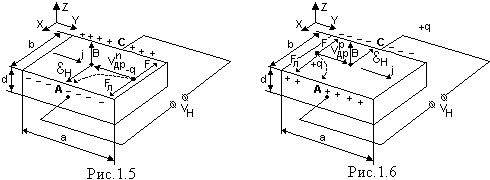азывается постоянной Холла, тогда V_H = R_HBjb и

, (1.20)

где J – ток, протекающий через пластинку.

Для полупроводников р-типа направление дрейфа дырок совпадает с направлением тока. Сила Лоренца в этом случае будет направлена по оси Х, так как изменяются одновременно и знак, и направление дрейфа (рис.1.6). Но теперь эта сила действует на положительно заряженные частицы, и поэтому точка А окажется под положительным потенциалом относительно точки С. Следовательно, по знаку холловской э.д.с. можно определить знак носителей заряда в полупроводнике. Условились считать знак R_Hположительным, когда ток переносится дырками, и отрицательным, когда он переносится электронами. Поэтому в формуле (1.19) стоит знак минус. Для полупроводников р-типа

. (1.21)

В случае собственных полупроводников с n_o= р_o= n_iпостоянная Холла определяется более сложным соотношением

(1.22)

Для большинства полупроводников µ_n> µ_pи знакRⁱ_H, как правило, является отрицательным.

18

постоянной Холла от температуры полностью определяется температурной зависимостью концентрации носителей заряда. На рис.1.7.а показана зависимость от Т концентрации носителей и на рис.1.7.б – постоянной Холла в соответствующих координатах. Кривая 1 на рис.1.7.б отвечает полупроводнику n-типа, а кривая 2 – полупроводнику р-типа. В области примесной проводимости для полу-проводника р-типа R_H> 0, в области собственной проводимости R_H< 0, так как µ_n> µ_р. Поэтому при переходе к собствен-ной проводимости R_Hменяет знак, переходя через нуль, а логарифм R_Hустремляется при этом к - ∞.

Эффект Холла является мощным экспериментальным средством изучения свойств носителей заряда в полупроводниках.

Измерив постоянную Холла, можно определить концентрацию носителей заряда в примесных полупроводниках, используя формулы (1.19) и (1.21), а по направлению э.д.с. Холла определить их знак. Знание R_Hпозволяет определить подвижность носителей заряда. Умножив R_Hна проводимость σ = qµ_n, получим

Rⁿ_Hσ = µ_n. (1.23)

Значение σ определяется соотношением

, (1.24)

где V – напряжение, прикладываемое к пластинке. Измерения R_Hот Т позволяют определить зависимость концентрации носителей заряда и их подвижности от температуры.

П р а к т и ч е с к а я ч а с т ь

Описание лабораторной установки

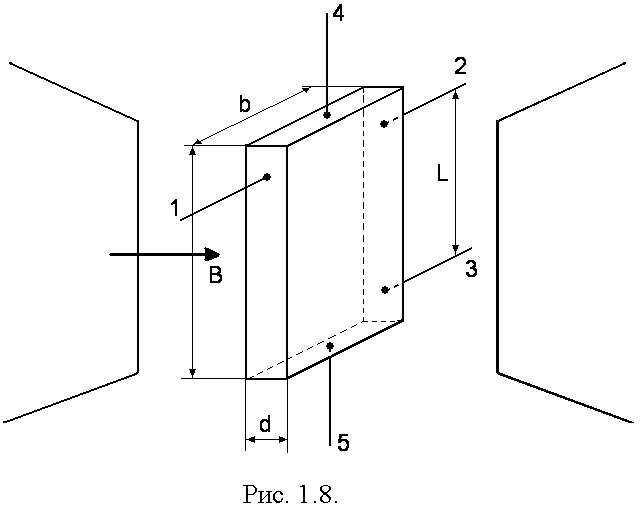
В лабораторной работе используются два образца полупроводниковых кристаллов из германия: собственный и с проводимостью р-типа с размерами: длина а, ширина bи толщинаd. Образцы помещены в термостат и находятся в зазоре магнитопровода постоянного магнита. Размещение одного из кристаллов относительно магнитного поля показано на рис. 1.8. Через контакты 4 и 5 пропускается постоянный ток величинойj. Контакты 2 и 3, расстояние между которыми равноL, служат для измерения продольной разности потенциаловU_C, по которой определяется проводимость образцов.

(1.25)

При измерении напряжения Холла V_Нна контактах 1 и 2 при В=0 имеется разность потенциалов, обусловленная неэквипотенциальностью расположения контактов 1 и 2, которая обозначается какU_Н. Поэтому для измерения необходимо определить на контактах 1 и 2 сначалаU_Нпри В=0, а затем напряжениепри включенном магнитном поле, и разность

V_H=-U_Н(1.26)

Значения напряжений U_C,U_Н,считываются со стрелочного индикатора “ИзмерениеU”. Под индикатором находятся кнопки переключения измеряемых напряжений на образцах 1 и 2 с указанием пределов шкалы индикатора.

Измерение напряжений производится при включении тумблера “Измерение”. После проведения очередного измерения тумблер надо обязательно выключить. Включение магнитного поля производится кнопкой.

Включение термостата для нагрева образцов полупроводников производится тумблером “Термостат”. Изменение температуры нагрева осуществляется потенциометром и контролируется стрелочным индикатором “Измерение T”, шкала которого отградуирована в градусах Цельсия. При включении термостата загорается сигнальная лампочка. Нагрев образцов до установленной температуры определяется по миганию сигнальной лампочки. Прежде чем приступить к измерениям после начала мигания лампочки необходима минутная выдержка.

Включение прибора в сеть осуществляется тумблером “Сеть – Вкл”.

Исходное положение переключателей: тумблер “Измерение” – “Выкл”, тумблер “Термостат” - “Выкл”, потенциометр установки температуры в крайнем левом положении.

Исходные данные для расчетов:L=7мм,b=2 мм,d=2 мм,J=5mA, В=1 Тл,q=1,6е-19 Кл,n_i=2,4е19 м^-3,k=1,38е-23 Джград.

Порядок выполнения работы

1. Измерение проводимости и постоянной Холла в зависимости от температуры. (Измерения проводятся при двух значениях температуры, указанных преподавателем.)

а) Включить прибор в сеть. Установить потенциометром по шкале индикатора температуру 30⁰С. Включить термостат. После начала мигания сигнальной лампочки термостата прогреть прибор в течении пяти минут. При выполнении работы периодически проверять установку температуры и при необходимости производить ее корректировку.

б) Нажать кнопку Ucдля образца 1. Включить тумблер “Измерение”. Записать показания прибора в таблицу 1. Выключить тумблер “Измерение”.

Таблица 1

T 0С	T К	образец 1					образец 2
		UC mV	 1 Ом м	UH mV	mV	VH mV	UC mV	 1 Ом м	UH mV	mV	VH mV
Т1
Т2

в) Нажать кнопку U_Ндля образца 1. Включить тумблер “Измерение”. Записать показания прибора в таблицу.

г) При нажатой кнопке включения магнитного поля, зарегистрировать показания прибораи занести в таблицу. Отпустить кнопкуивыключить тумблер “Измерение”.

д) Нажать кнопку U_Cдля образца 2. Выждать одну минуту. Включить тумблер “Измерение”. Считать показания прибора,обращая внимание на пределы шкалы. Занести показания в таблицу.Выключить тумблер “Измерение”.

е) Нажать кнопку U_Hдля образца 2. Включить тумблер “Измерение”. Записать показания прибора в таблицу,обращая внимание на пределы шкалы.

ж) При нажатой кнопке включения магнитного поля, зарегистрировать показания прибораи занести в таблицу. Отпустить кнопкуивыключить тумблер “Измерение”.

з) Установить потенциометром второе значение температуры, заданное преподавателем. Дождаться начала мигания лампочки термостата. Выждать одну минуту. Приступить к измерениям согласно пунктам б) – ж).

Выключить установку.

2. Рассчитать по формулам (1.25) и (1.20) значения ,ln,R_H и занести их в таблицу 2.

Таблица 2

T К	образец 1			образец 2
	 1 Ом м	ln	RH м3Кл	 1 Ом м	ln	RH м3Кл
Т1
Т2

3. По полученным значениям построить графики ln=f(1T) и определить какой образец полупроводникового кристалла является собственным, а какой примесным.

4. Для собственного полупроводника по графику ln=f(1T) и данным таблицы 2 определить ширину запрещенной зоны германия ΔЕg(эВ) по формуле

(эВ)

5. Последующие пункты выполняются по заданию преподавателя.

а) По формуле (1.23) для примесного полупроводника рассчитать подвижность дырок при T=30⁰С.

б) По формуле (1.22) при температуре 30⁰С определить подвижность электронов в собственном полупроводнике, используя значение подвижности для дырок для примесного полупроводника при 30⁰С.

в) Из формулы для R_Н для примесного полупроводника определить концентрацию основных носителей заряда; используя закон действующих масс определить концентрацию неосновных носителей заряда.

6. Оформить отчет.

Содержание отчета

1. Цель и задачи исследования.

2. Основные рабочие формулы.

3. Результаты эксперимента в виде таблиц и графиков.

4. Результаты расчетов.

5. Анализ полученных данных и выводы по работе.

Контрольные вопросы

1. Зависимость концентрации носителей заряда в собственном полупроводнике от температуры.

2. Зависимость концентрации носителей заряда в примесном полупроводнике от температуры.

3. Чем определяется значение температуры истощения примеси и температуры перехода к собственной проводимости.

4. Зависимость проводимости полупроводника от температуры.

5. Эффект Холла.

6. Зависимость постоянной Холла от температуры.

7. Что позволяют определить и почему температурные зависимости проводимости полупроводника и постоянной Холла.

Лабораторная работа № 2

ИССЛЕДОВАНИЕ ФОТОПРОВОДИМОСТИ ПОЛУПРОВОДНИОВ

Цель работы: теоретическое изучение явлений генерации и рекомбинации неравновесных носителей заряда, фотопроводимости и экспериментальное определение спектральных характеристик полупроводников и времени жизни неравновесных носителей заряда.

Т е о р е т и ч е с к а я ч а с т ь