
Рейтинг и вопросы математика2. Стрежнева
.doc
|
Рейтинговая оценка курса «Математика» 1 семестр 1 курс (осень) (из 100 возможных баллов) 1 аттестация - 20 баллов 1) Самостоятельная работа на тему «Комплексные числа» - 5 баллов (Зачтена, если набрано не менее 3 баллов) 2) Коллоквиум на тему «Числовые последовательности и комплексные числа» - 15 баллов (5 баллов диктант и 10 баллов билет) [коллоквиум зачтен, если набрано не менее 7 баллов (2+5))]
2 аттестация – 30 баллов 1) Контрольная работа «Пределы» - 10 баллов (зачтена, если набрано не менее 5 баллов) 3) Контрольная работа «Производная» - 10 баллов (зачтена, если набрано не менее 5 баллов) 4) Контрольная работа «Неопределенный интеграл» - 10 баллов (зачтена, если набрано не менее 5 баллов) 3 аттестация – 50 баллов 1) Коллоквиум «Функции одной действительной переменной: предел функции в точке, непрерывность, точки разрыва. Дифференциальное исчисление функций одной действительной переменной и его приложения. Неопределенный интеграл» - 50 баллов (10 баллов диктант и 40 баллов билет). Коллоквиум зачтен, если набрано не менее 26 баллов (6+20). Аттестации считаются успешно пройденными, если
Экзаменационная оценка курса:
Если
P.S. Диктант по определениям состоит из 20 вопросов. Если набрано 14 и больше верных ответов (70%), то диктант зачитывается.
|
Программа.
ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ ПО ВЫСШЕЙ МАТЕМАТИКЕ
(1 курс, осенний семестр). МАТЕМАТИЧЕСКИЙ АНАЛИЗ.
-
Коллоквиум №1 на тему «Числовые последовательности и комплексные числа» - 15 баллов
-
Логическая символика.
-
Множества и простейшие операции над множествами.
-
Числовые множества (N, Q, J, R). Геометрическая интерпретация множества действительных чисел (числовая ось, числовая прямая, расширенная числовая ось (прямая)). Важнейшие числовые множества действительных чисел: промежутки (отрезок, интервал, полуинтервал), неограниченные промежутки, окрестности.
-
Понятие эквивалентности множеств, мощности множеств.
-
Счетные и несчетные множества. Свойства счетных множеств. Континуум.
-
Множество комплексных чисел. Понятие аргумента комплексного числа и его главного значения. Понятие мнимой единицы. Формы записи комплексного числа. Алгебраические операции над комплексными числами.
-
Абсолютная величина (модуль) действительного числа. Свойства абсолютной величины.
-
Понятие числовой последовательности, способы задания, примеры.
-
Геометрическое изображение членов последовательности.
-
Последовательности, ограниченные сверху (снизу). Ограниченные и неограниченные числовые последовательности, геометрическая иллюстрация.
-
Предел числовой последовательности (определение на языке кванторов). Геометрический смысл предела числовой последовательности. Предельная точка. Определение номера
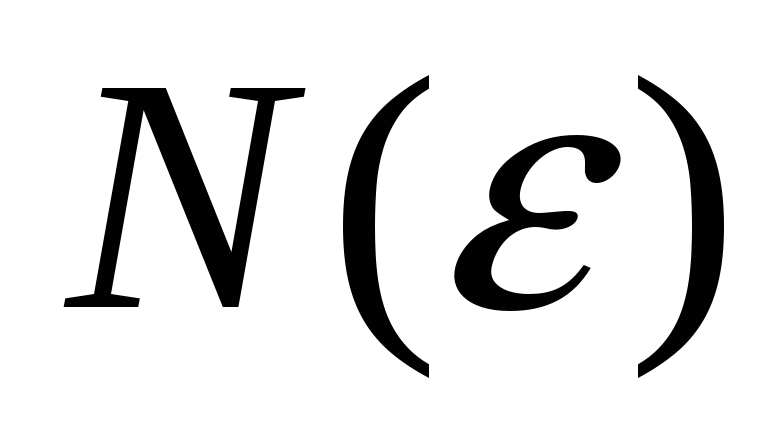 по
по
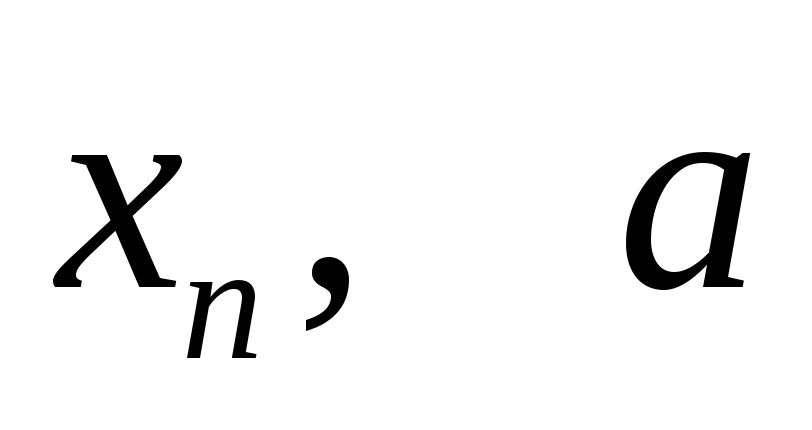 .
Пример
.
Пример
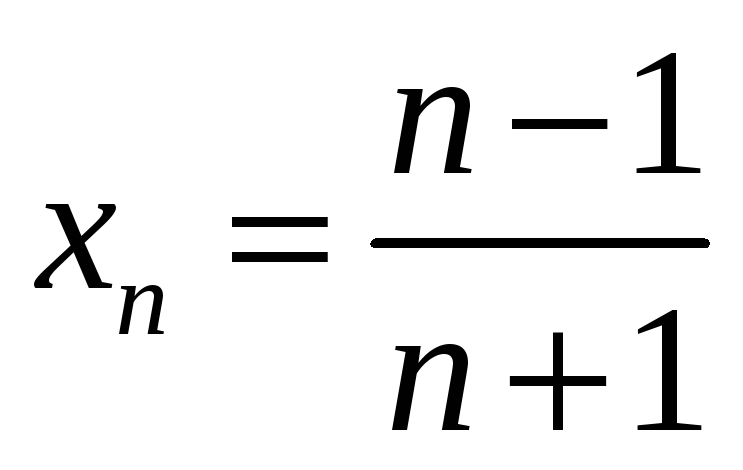 .
.
-
Сходящиеся и расходящиеся последовательности. Необходимое условие сходимости и достаточное условие расходимости числовой последовательности.
-
Сходящиеся последовательности и их свойства.
-
Основные операции над последовательностями.
-
Бесконечно малые последовательности. Основные свойства бесконечно малых последовательностей.
-
Бесконечно большие последовательности, их свойства.
-
Теорема о связи бесконечно больших и бесконечно малых последовательностей.
-
Необходимое и достаточное условие сходимости числовой последовательности к пределу "а".
-
Теоремы о конечных пределах и о предельных переходах в неравенствах.
-
Теорема о сжатой последовательности.
-
Точная верхняя и точная нижняя грань числовой последовательности.
-
Монотонные последовательности.
-
Критерий Вейерштрасса о сходимости монотонной последовательности.
-
Неравенство Бернулли. Понятие числа
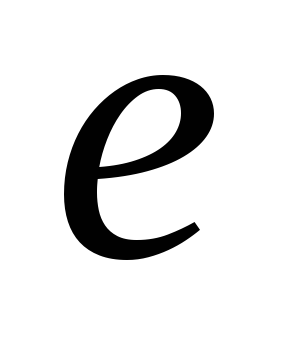 .
Фундаментальные последовательности.
Критерий Коши.
.
Фундаментальные последовательности.
Критерий Коши.
-
Коллоквиум №2 «Функции одной действительной переменной:
предел функции в точке, непрерывность, точки разрыва.
Дифференциальное исчисление функций одной действительной переменной и его приложения. Неопределенный интеграл» - 50 баллов
-
Числовая функция: определение, способы задания, основные характеристики поведения (четность, периодичность, монотонность и т.д.), сложная функция, ограниченная функция.
-
Основные элементарные функции. Класс элементарных функций.
-
Предел функции в точке: определение по Коши, определение по Гейне, геометрическая иллюстрация.
-
Эквивалентность определений предела функции в точке по Коши и по Гейне.
-
Левый и правый предел функции в точке, геометрическая иллюстрация. Теоремы о левом и правом пределе, о единственности предела, о конечных пределах.
-
Предел функции в бесконечности, геометрическая иллюстрация. Бесконечно большие функции и их свойства.
-
Бесконечно малые функции, их свойства. Сравнение бесконечно малых функций.
-
Первый и второй замечательные пределы.
-
Непрерывность функции в точке, геометрическая иллюстрация. Основные элементарные функции. Теорема о непрерывности элементарных функций.
-
Точки разрыва функции и их классификация.
-
Понятие производной функции в точке. Геометрическая иллюстрация точек, в которых производная не существует.
-
Связь дифференцируемости и непрерывности функции.
-
Таблица производных, основные правила дифференцирования, производная сложной и неявно заданной функции. Логарифмическое дифференцирование.
-
Производная обратной и параметрически заданной функции.
-
Уравнение касательной и нормали к кривой.
-
Приложение дифференциала к приближенным вычислениям.
-
Производные высших порядков.
-
Дифференциалы высших порядков. Теорема об инвариантности дифференциала 1-го порядка.
-
Свойства функций непрерывных на отрезке.
-
Дифференцируемые в интервале функции: теоремы Ролля, Лагранжа, Коши.
-
Правило Лопиталя и его применение.
-
Формулы Тейлора и Маклорена, разложение элементарных функций по формуле Тейлора и Маклорена.
-
Монотонные функции. Теорема о взаимосвязи характера монотонности дифференцируемой на интервале функции со знаком производной.
-
Внутренние локальные экстремумы функции: понятие и геометрический смысл.
-
Необходимый признак существования экстремума функции.
-
Первый достаточный признак существования локального экстремума для непрерывной функции.
-
Второй достаточный признак существования экстремума функции в терминах высших производных.
-
Отыскание наибольшего и наименьшего значений функции на отрезке.
-
Выпуклые и вогнутые функции. Критерий строгой выпуклости (вогнутости) функции.
-
Критерий строгой выпуклости (вогнутости) для дважды дифференцируемой в интервале функции.
-
Понятие точки перегиба. Необходимый признак существования у функции точки перегиба.
-
Первый и второй достаточные признаки существования у функции точек перегиба.
-
Асимптоты к графику функции и способы их отыскания.
-
Алгоритм исследования функции и построения ее графика.
-
Понятие первообразной, терема о структуре первообразных, геометрическая иллюстрация.
-
Понятие неопределенного интеграла и его свойства.
-
Непосредственное интегрирование (таблица неопределенных интегралов). Интегрирование гиперболических функций.
-
Подведение функции под знак дифференциала, метод подстановки.
-
Интегрирование по частям. Таблица некоторых интегралов к которым применим метод интегрирования по частям.
-
Понятие рациональной дроби (правильной и неправильной), теорема о связи неправильной и правильной рациональных дробей. Виды простейших рациональных дробей. Разложение правильной дроби на простейшие. Методы нахождения неопределенных коэффициентов: метод частных значений, метод сравнения неопределенных коэффициентов при одинаковых степенях, комбинированный метод.
-
Интегрирование простейших дробей I-IV типов. Правило нахождения интегралов от дробно-рациональных функций.
-
Метод Остроградского при интегрировании правильной рациональной дроби со знаменателем, имеющим кратные корни.
-
Интегрирование простейших иррациональных функций и биномиальных дифференциалов (таблица).
-
Интегрирование простейших тригонометрических функций (таблица).
-
Подстановки Эйлера.
-
Основные интегралы, которые не берутся в элементарных функциях.
Задачи
При выполнении практических заданий студенты должны уметь:
-
Переводить одну форму записи комплексного числа в другую, выполнять арифметические действия с комплексными числами, решать уравнения с комплексными корнями.
-
Находить пределы числовых последовательностей и функций .
-
Сравнивать бесконечно малые функции;
-
Исследовать функцию на непрерывность,
-
Определять характер точек разрыва;
-
Находить производные функций.
-
Применять правило Лопиталя для вычисления пределов.
-
Составлять уравнения касательной и нормали к кривой.
-
Раскладывать функцию по формуле Тейлора и Маклорена.
-
Находить наибольшее и наименьшее значение функции на отрезке.
-
Проводить полное исследование функции и строить ее график.
-
Вычислять неопределенные интегралы.
Примерные вопросы для диктанта на коллоквиуме №1 (вопросы могут быть другими! Это лишь примерный образец)
-
Дайте определение множества комплексных чисел.
-
Дайте определение аргумента комплексного числа и его главного значения.
-
Запишите формулу для нахождения главного значения аргумента комплексного числа в пределах
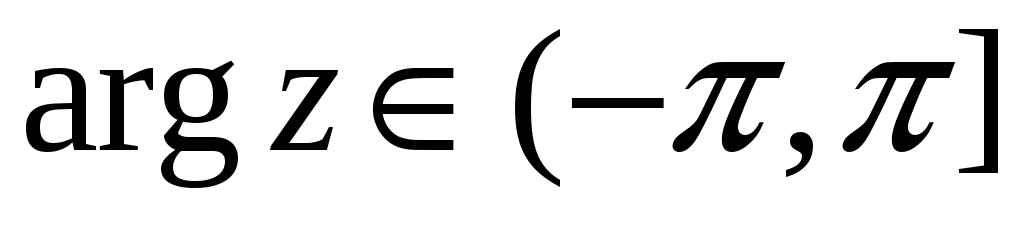 .
. -
Запишите три формы записи комплексного числа.
-
Формула Муавра.
-
Формула для нахождения корня из комплексного числа.
-
Дайте определение предела числовой последовательности на языке кванторов:
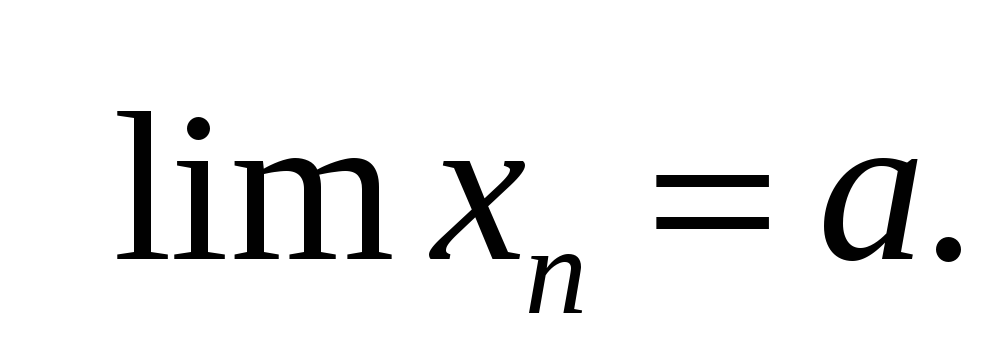
-
Дайте определение сходящейся числовой последовательности.
-
Дайте определение бесконечно малой числовой последовательности (словами и на языке кванторов).
-
Дайте определение бесконечно большой числовой последовательности….
-
Дайте определение ограниченной числовой последовательности на языке кванторов.
-
Сформулируйте необходимый признак сходимости числовой последовательности.
-
Сформулируйте достаточный признак расходимости числовой последовательности.
-
Дайте определения 4-х видов монотонных последовательностей: название — неравенство.
-
Дайте определение точной верхней грани числовой последовательности (
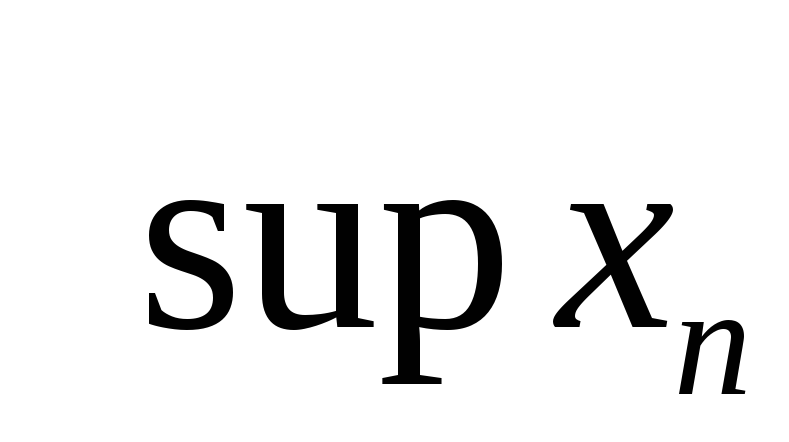 )
и точной нижней грани (
)
и точной нижней грани (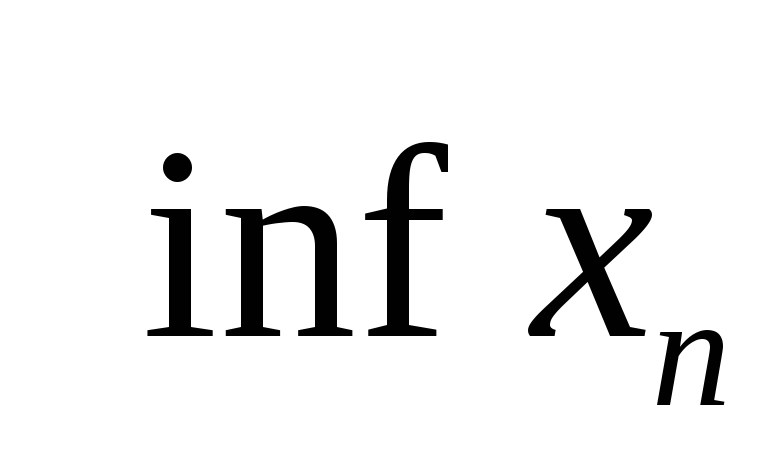 ).
). -
Сформулируйте критерий Вейерштрасса о сходимости монотонной последовательности.
-
Сформулируйте теорему о связи сходящейся последовательности с бесконечно малой.
-
Сформулируйте теорему о связи бесконечно малой и бесконечно большой последовательностей.
-
Дайте определение числа e (экспоненты).
-
Дайте определение фундаментальной числовой последовательности на языке кванторов.
-
Сформулируйте критерий Коши о сходимости фундаментальной последовательности.
-
Сформулируйте теорему о предельных переходах в неравенствах.
-
Сформулируйте теорему Коши о конечных пределах.
Примерные вопросы для диктанта на коллоквиуме №2 (вопросы могут быть другими!)
-
Запишите первый замечательный предел и следствия из него.
-
Запишите второй замечательный предел и следствия из него.
-
Дайте определение непрерывной функции на языке пределов.
-
Дайте определение непрерывной функции на языке кванторов.
-
Дайте определение непрерывной функции на языке приращений.
-
Дайте определение точки разрыва.
-
Дайте определение точки разрыва первого рода.
-
Дайте определение точки разрыва второго рода.
-
Дайте определение устранимого разрыва.
-
Дайте определение скачка.
-
Сформулируйте теорему Ролля.
-
Сформулируйте теорему Лагранжа.
-
Сформулируйте теорему Коши.
-
Сформулируйте правило Лопиталя.
-
Дайте определение точки максимума и минимума функции.
-
Сформулируйте необходимый признак экстремума функции.
-
Сформулируйте первый достаточный признак экстремума функции.
-
Сформулируйте второй достаточный признак экстремума функции.
-
Дайте определение выпуклой и вогнутой функции.
-
Сформулируйте критерий строгой выпуклости (вогнутости) графика функции.
-
Сформулируйте необходимый признак точки перегиба графика функции.
-
Сформулируйте первый достаточный признак существования у функции точки перегиба.
-
Сформулируйте второй достаточный признак существования у функции точки перегиба.
-
Дайте определение асимптоты графика функции.
-
Выпишите три вида асимптот и правила их нахождения.
-
Дайте определение первообразной.
-
Сформулируйте теорему о структуре всех первообразных.
-
Дайте определение неопределенного интеграла.
-
Запишите формулу интегрирования по частям.
-
Запишите виды интегралов, для которых применим метод интегрирования по частям и укажите, что в этих интегралах обозначается за
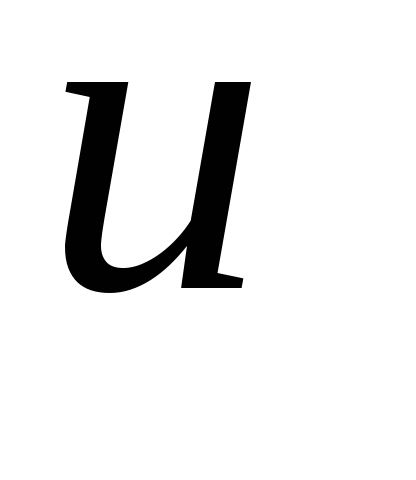 и за
и за
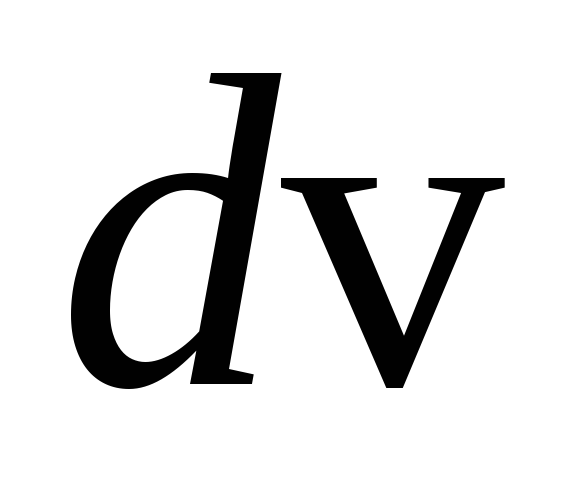 .
. -
Запишите четыре вида простейших дробей со всеми ограничениями.
-
Дайте определение рациональной дроби.
-
Какая рациональная дробь называется правильной, а какая нет?
-
Сформулируйте правило разложения правильной рациональной дроби на простейшие.
-
В чем состоит метод частных значений для нахождения неопределенных коэффициентов при разложении правильной рациональной дроби на простейшие?
-
В чем состоит метод сравнения коэффициентов при одинаковых степенях
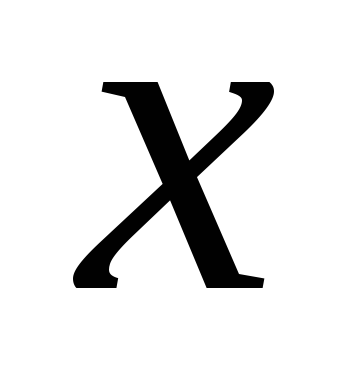 для нахождении неопределенных
коэффициентов при разложении правильной
рациональной дроби на простейшие?
для нахождении неопределенных
коэффициентов при разложении правильной
рациональной дроби на простейшие? -
В чем состоит комбинированный метод для нахождения неопределенных коэффициентов при разложении правильной рациональной дроби на простейшие?
-
Какая замена применяется при интегрировании простейшей дроби третьего типа (метод выделения полного квадрата).
-
Какой метод интегрирования используется при интегрировании простейшей дроби четвертого типа (для получения рекуррентного соотношения).
-
Запишите универсальную тригонометрическую подстановку. Как через нее выражаются тригонометрические функции
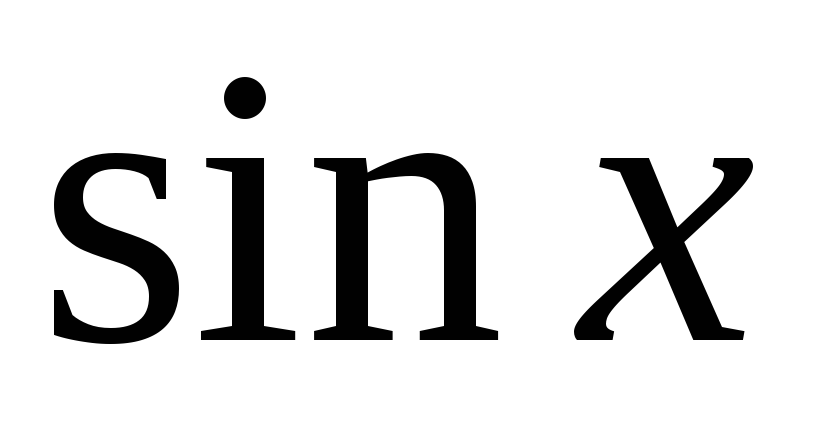 и
и
 .
. -
Какая замена применяется при вычислении интеграла вида
 ,
,
 — рациональная функция, если
подынтегральной тригонометрическое
выражение нечетно относительно функции
— рациональная функция, если
подынтегральной тригонометрическое
выражение нечетно относительно функции
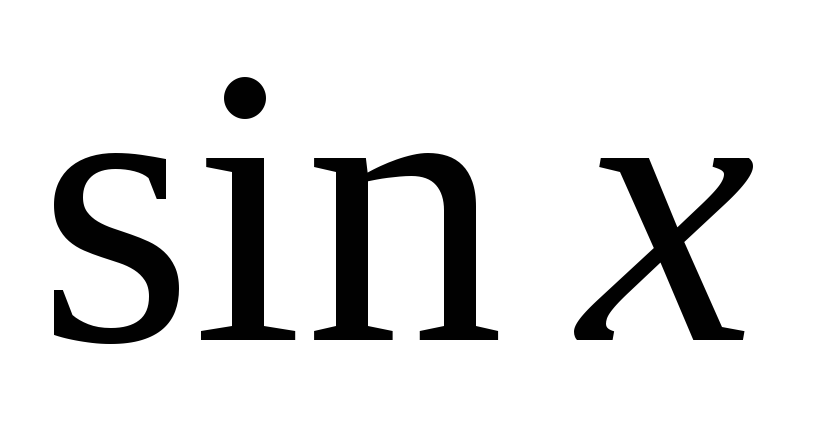 :
:
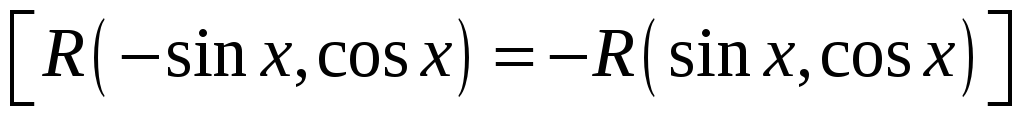 ?
? -
Какая замена применяется при вычислении интеграла вида
 ,
,
 — рациональная функция, если
подынтегральной тригонометрическое
выражение нечетно относительно функции
— рациональная функция, если
подынтегральной тригонометрическое
выражение нечетно относительно функции
 :
:
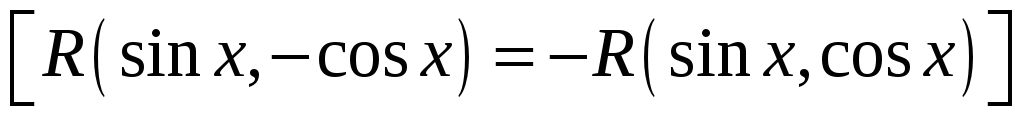 ?
? -
Какая замена применяется при вычислении интеграла вида
 ,
,
 — рациональная функция, если
подынтегральной тригонометрическое
выражение четно относительно функций
— рациональная функция, если
подынтегральной тригонометрическое
выражение четно относительно функций
 и
и
 :
:
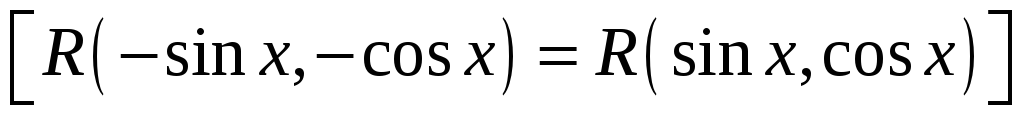 ?
? -
С помощью каких трех формул (понижения степени) вычисляется интеграл вида
 ,
где m и n
– четные неотрицательные целые числа.
,
где m и n
– четные неотрицательные целые числа. -
С помощью последовательного применения какой формулы вычисляется интеграл
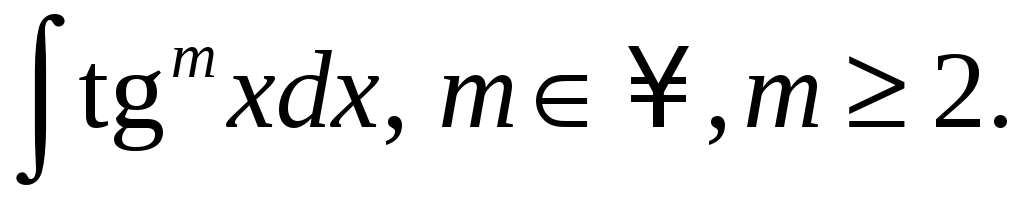
-
С помощью последовательного применения какой формулы вычисляется интеграл
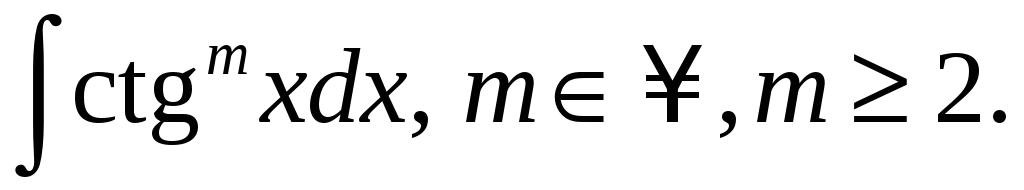
-
Укажите при помощи какой замены вычисляется интеграл
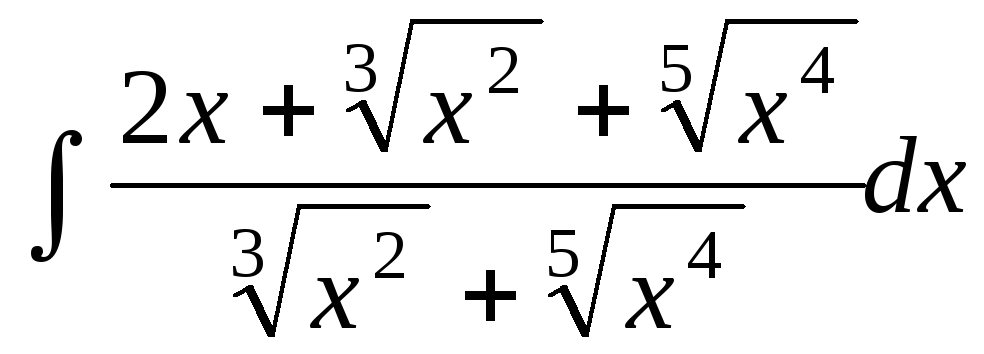 .
. -
Укажите при помощи какой замены вычисляется интеграл
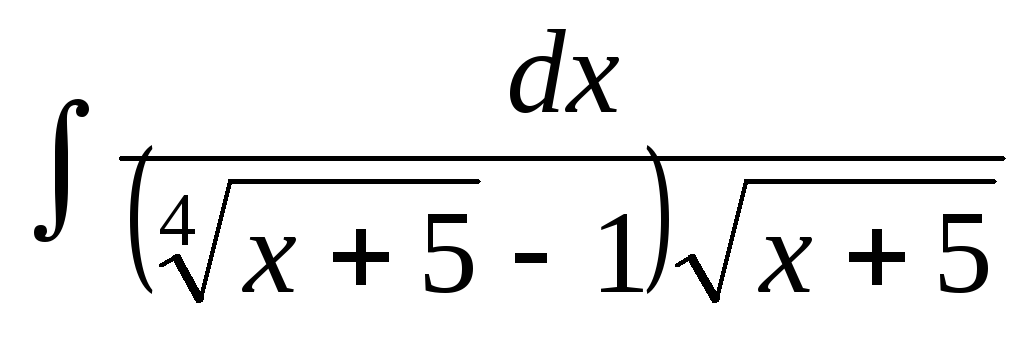 .
. -
Укажите при помощи какой замены вычисляется интеграл
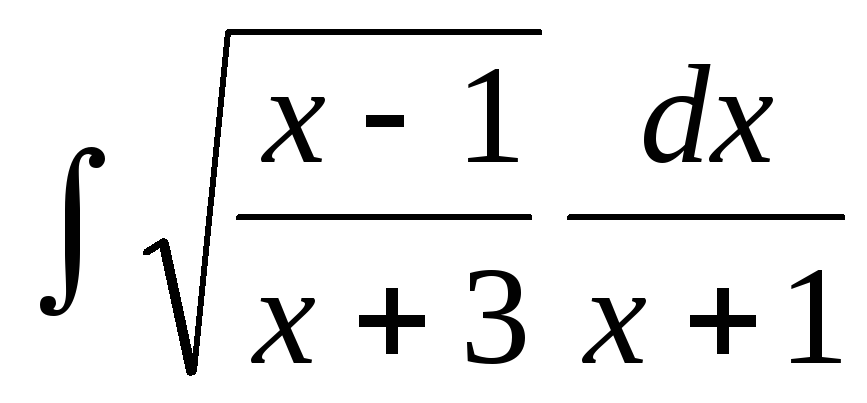
-
Какие тригонометрические замены используются при интегрировании иррациональных выражений вида
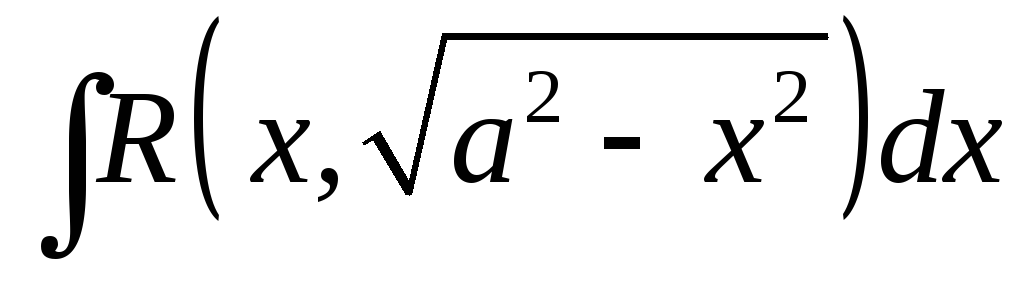 ,
,
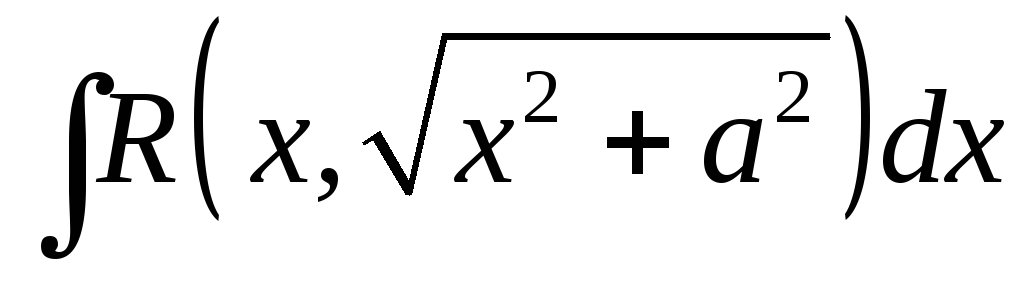 ,
,
 .
. -
Как выделить полный квадрат для интеграла
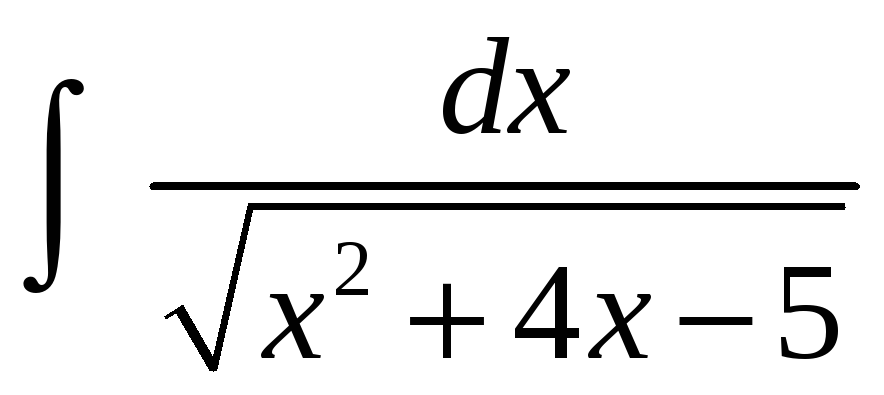 .
Укажите соответствующую замену.
.
Укажите соответствующую замену. -
Запишите формулу приведения Остроградского для интеграла
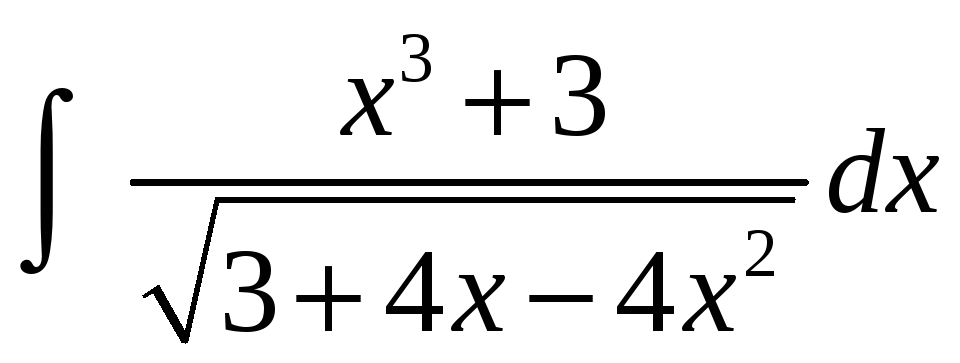 .
Неопределенные коэффициенты не
находите.
.
Неопределенные коэффициенты не
находите. -
Укажите обратную замену для интеграла
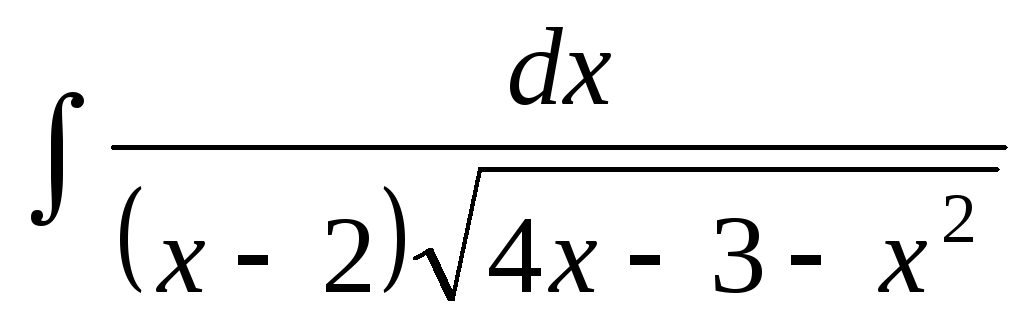 .
. -
Дайте определение дифференциального бинома и укажите все подстановки Чебышева, которые применяются для его интегрирования.
-
Запишите с названиями все интегралы, не берущиеся в элементарных функциях.
Учебно-методическое обеспечение дисциплины.
Рекомендуемая литература
а) основная литература:
-
Ильин В.А., Позняк Э.Г. Основы математического анализа. Т 1, 2. М.: Физматлит. 2002.
-
Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т 1,2. М.: Наука. 2000.
-
Дорофеева С.И., Дараган М.А. Пределы и дифференциальное исчисление функций одной переменной. Казань. КГТУ. 2003.
-
Письменный Д.Т. Конспект лекций по высшей математике. Ч. 1,2. М. Айрис Пресс. 2006.
-
Шипачев В.С. Высшая математика. М. Высшая школа. 2004.
-
Данко П.Е., А.Г. Попов, Т.Я. Кожевникова. Высшая математика в упражнениях и задачах. М.: «ОНИКС 21 век», 2003.
-
Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. М.: Наука. 2003.
-
Гусак А.А. Высшая математика в двух томах. Минск: ТатраСистемс. 2004.
-
Миносцев В.Б. Курс высшей математики. М.: МГИУ. 2005.
-
Берман Н.Г. Сборник задач по курсу математического анализа. М.: Наука. 2006.
-
Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). Краснодар: Лань. 2005.
-
Сборник задач по математике для втузов в 4 частях / под общей ред. Ефимова А.В. М.: Физ. мат. лит, 2003.
-
Стрежнев В.А., Исхаков Э.М., Шабалина С.Б., Дараган М.А., Насырова Е.В., Соловьев В.В., Дорофеева С.И., Бильченко Н.Г. Высшая математика, программа, методические указания и контрольные задания. Ч.1.Казань.: изд-во КГТУ им. А.Н. Туполева, 2000.
б) дополнительная литература:
-
Дараган М.А., Миронова СР., Исхаков Э.М. Пределы. Дифференциальное исчисление функции одной переменной. Казань.: КАИ. 1994. 50 экз.
-
Дараган М.А., Дорофеева С.И., Соловьев В.В., Стрежнев В.А. Пределы. Дифференциальное исчисление функций одной переменной. Практикум по высшей математике. Казань: КАИ. 1992.
-
Фихтенгольц Г.М. Основы математического анализа. С-Пб.: изд-во «Лань», 2001.
-
Демидович Б.П. Краткий курс высшей математики. М.: ООО изд-во «Астрель», 2001.
-
Кудрявцев Л.Д. Курс математического анализа. М.: Дрофа. 2003. Т. 1,2,3.
-
Рождественский Б.Л. Лекции по математическому анализу. М.: Наука. 1972.
-
Смирнов В.И. Курс высшей математики. М.: Наука. 1974.
-
Бугров Я.С. Сборник задач по высшей математике. Учебное пособие для ВУЗов. Ростов: изд-во «Феникс», 1997.

