лаба4
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Информатика»
Лабораторная работа №4
«Численное интегрирование»
Выполнил: ---------------------------------------------
Проверил:
Москва, 2023 г.
Пример индивидуального задания
№ |
Подынтегральная функция |
a |
b |
t |
m |
|
8 |
f(x) = x sin(x+1) – cos(x-5) |
1 |
2 |
1 |
2 |
0.25 |
Задания для численного интегрирования:
x*sin(x+1) – cos(x-5) - подынтегральная функция;
a=1, b=2 – пределы интегрирования;
методы интегрирования – средних прямоугольников, трапеций;
начальный шаг интегрирования
Вычисление интегралов с шагом и /2 (
и
/2)
и оценка его погрешности по правилу
Рунге
Правило
Рунге применяют для вычисления погрешности
путём двойного просчёта интеграла с
шагом h/2
и h,
при этом погрешность вычисляется по
формуле
.
Полагаю,
что интеграл вычислен с точностью E,
если
;
тогда I=
,
где I
– уточнённое значение интеграла, p
– порядок метода.
Вычислим интеграл по формуле
трапеций и оценим погрешность интегрирования методом двойного просчёта:
Шаг =0.25:
n
=
=
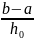= 4
=
Шаг
=
0.125:
n
=
=
= 8
=
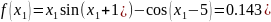
Теперь мы можем посчитать оценку погрешности метода трапеций:
=
= 0.319 – оценка погрешности метода
трапеций.
I
=
;
I
= 1.924 + 0.319 = 2.243
Метод средних прямоугольников методом на языке C++ #include <iostream>
#include <math.h>
#include <cmath>
#include <iomanip>
using namespace std;
double f(double x) {
return x * sin(x + 1) - cos(x - 5);
}
double RectangleIntegral(double a, double b, double h) {
double x, fx;
double sum = 0;
double n = (b - a) / h;
for (int i = 0; i < n; i++) {
x = a + i * h;
fx = f(x + h / 2);
sum += fx;
}
return sum * h;
}
int main() {
setlocale(LC_ALL, "Russian");
cout.setf(ios::left | ios::fixed);
double a = 1, b = 2, eps = 0.319, h = 0.25;
double IPrev, I, R, IRefined;
IPrev = RectangleIntegral(a, b, h);
do {
h = h / 2;
I = RectangleIntegral(a, b, h);
R = (I - IPrev) / 3;
IRefined = I + R;
cout << "I(h=" << h * 2 << ")" << " I(h = " << h << ")" << " R" << " I" << endl;
cout << setw(15) << IPrev << setw(15) << I << setw(15) << R << IRefined << endl;
IPrev = I;
} while (abs(R) >= eps);
system("PAUSE");
}
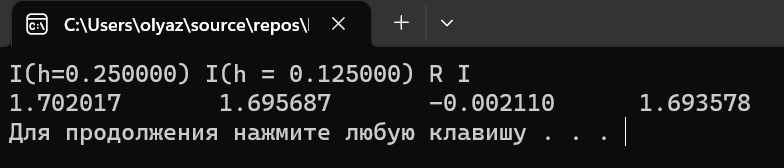
Результат работы программы
Расчёт
в среде Scilab
