
лаба1
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»

Кафедра «Информатика»
Лабораторная работа №1
«Методы решения нелинейного уравнения»
Выполнил: ---------------------------------------------
Проверил:
Москва, 2023 г.
Пример индивидуального задания
![]()
![]()
Методы: 2 – итерации; 3 – Ньютона;
Результат выполнения задания:
--> //Строим график нашей функции y=cos(x)–sqrt(x + 2) + 1 = 0 на отрезке [0.1:1]
--> scf(1);
--> deff('y=fdraw(x)','y=cos(x)-sqrt(x+2)+1');
--> x=[0.1:0.1:1];
--> plot(x,fdraw(x),'LineStyle','-','Color','red','Thickness',...
> 3,'Marker','0','MarkerEdgeColor','black','MarkerFaceColor',...
> 'yellow','MarkerSize',3)
--> plot(x,0,'LineStyle','--','Color','blue','Thickness',3)
--> xtitle('Графики функции f1(x)','X')
--> legend('Функция f(x)')
ans =
Handle of type "Legend" with properties:
========================================
parent: Axes
children: []
visible = "on"
text = "Функция f(x)"
font_style = 6
font_size = 1
font_color = -1
fractional_font = "off"
links = "Polyline"
legend_location = "in_upper_right"
position = [0.6592213,0.1325]
line_width = 0.1
line_mode = "on"
thickness = 1
foreground = -1
fill_mode = "on"
background = -2
marks_count = 3
clip_state = "off"
clip_box = []
user_data = []
tag = ""
--> xgrid
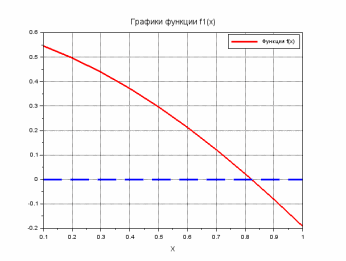
Вывод: Из графика видно, что на отрезке [0,1:1] уравнение имеет один корень.
--> //Отделяем корни
--> function s=fi(x)
> deff('y=f(x)','y=cos(x)-sqrt(x+2)+1');
> deff('y=f1(x)','y=-sin(x)-(1/(2.*sqrt(x+2)))'); //1-ая производная
> deff('y=f2(x)','y=(1/((4*x+8)*(sqrt(x+2))))-cos(x)'); //2-ая производная
> s=[x,f(x),f1(x),f2(x)];
> end
--> //Создаем массив и задаем значение X
--> p=zeros(5,4);x=0.1:0.1:1;
--> //Заполняем массив корнями уравнений
--> for i=1:10
> p(i,:)=fi(x(i));
> end
--> //Выводим наш массив
--> disp(p)
0.1 0.5458665 -0.4448662 -0.9128535
0.2 0.4968269 -0.5357693 -0.903453
0.3 0.4387614 -0.6252104 -0.8836647
0.4 0.3718677 -0.712167 -0.8538217
0.5 0.2964437 -0.7956533 -0.814337
0.6 0.2128841 -0.8747293 -0.7657035
0.7 0.1216745 -0.948508 -0.7084921
0.8 0.0233867 -1.0161632 -0.6433483
0.9 -0.0813287 -1.076937 -0.5709875
1. -0.1917485 -1.1301461 -0.4921898
Вывод: На концовках отрезка [0.1;1] функция имеет противоположные знаки, а1-я производная знакопостоянна, что является проверкой выполнения условия сходимости, следовательно, на этом отрезке уравнения имеет единственный корень.
Решение методом итерации (метод последовательных приближений)
Метод итераций (или метод простых итераций) - это численный метод для решения нелинейных уравнений. Он заключается в том, чтобы последовательно вычислять значения функции на каждой итерации и использовать предыдущее значение в качестве начального приближения на следующей итерации, пока значение функции не станет достаточно близко к искомому решению.
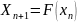
Здесь мы определяем начальное значение ‘x’, точность ‘eps’ и максимальное число итераций ‘max_iter’. Затем мы используем цикл ‘for’ для выполнения итераций. На каждой итерации мы вычисляем функцию и ее производную в точке ‘x’, находим новое значение ‘x’ и сравниваем разницу между старым и новым значением с точностью ‘eps’. Если разница меньше точности, то мы нашли корень и выходим из цикла. В конце мы проверяем, был ли найден корень в заданном количестве итераций, и выводим сообщение об ошибке, если не был найден.
Код сценария iteration.sce
--> x = 0.0;
--> eps = 1e-6;
--> max_iter = 1000;
--> printf("Iteration\t x\t\t diff\n");
--> for i = 1:max_iter
> f_x = cos(x) - sqrt(x + 2) + 1;
> f_derivative_x = -sin(x) - (1 / (2 * sqrt(x + 2)));
> x_new = x - f_x / f_derivative_x;
> diff = abs(x_new - x);
> printf("%d\t\t %.8f\t %.8f\n", i-1, x_new, diff);
> if diff < eps
> break;
> end
> x = x_new;
> end
Iteration x diff
0 1.65685425 1.65685425
1 0.86319140 0.79366285
2 0.82331961 0.03987179
3 0.82285080 0.00046882
4 0.82285073 0.00000007
Iteration |
x |
diff |
0 |
1.65685425 |
1.65685425 |
1 |
0.86319140 |
0.79366285 |
2 |
0.82331961 |
0.03987179 |
3 |
0.82285080 |
0.00046882 |
4 |
0.82285073 |
0.00000007 |
Решение методом Ньютона на языке программирования C++
Для
заданного уравнения
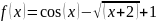
Производная
будет иметь вид
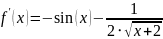
#include <iostream>
#include <cmath>
using namespace std;
double f(double x) {
return cos(x) - sqrt(x + 2) + 1;
}
double f_derivative(double x) {
return -sin(x) - (1 / (2. * sqrt(x + 2)));
}
int main() {
double x0 = 0.0;
double eps = 1e-6;
int max_iter = 1000;
double x = x0;
int i = 0;
int iter = 0;
int innovations = 0;
while (i < max_iter) {
double f_x = f(x);
double f_derivative_x = f_derivative(x);
double x_new = x - f_x / f_derivative_x;
double diff = fabs(x_new - x);
cout << "Iteration: " << iter << ", x = " << x_new << ", diff = " << diff << endl;
if (diff < eps) {
cout << "Root found: " << x_new << endl;
cout << "Number of innovations: " << innovations << endl;
return 0;
}
innovations++;
x = x_new;
i++;
iter++;
}
cout << "Root not found within " << max_iter << " iterations" << endl;
return 0;
}
В этой реализации мы определили функцию f(x) и ее производную f_derivative(x) в соответствии с нашим уравнением. Затем мы добавили переменные iter и innovations для отслеживания номера текущей итерации и количества инноваций (количество раз, которое мы находим новое значение x) соответственно.
Внутри цикла мы вычисляем значения функции f(x) и ее производной f_derivative(x) в текущей точке x, а затем используем их для вычисления нового значения x_new в соответствии с методом Ньютона. Мы также выводим на экран текущее значение x_new, разницу между предыдущим и текущим значением (diff) и номер текущей итерации (iter).
Затем мы проверяем, достигли ли мы достаточной точности (то есть
