афанасьев

Лабораторная работа №1

Метод простой итерации. Метод Гаусса-Зейделя.

Выполнил: студент 2 курса, группы 32

Афанасьев Яков

Проверила: Кокурина Г.Н.

Иваново 2012

Метод простой итерации

Данная функция:

8x₁+2x₂-5x₃-3x₄=-91

-x₁-7x₂-3x₃-2x₄=-12

-8x₁+x₂-9x₃=-60

-5x₁+3x₂+5x₃-9x₄=-43

Теоретическая часть

В основе метода заложено понятие сжимающего отображения. Определим терминологию:

Говорят, что функция  осуществляет сжимающее отображение на , если

1. 

2. 

Тогда основная теорема будет выглядеть так:

Теорема Банаха (принцип сжимающих отображений). Если  — сжимающее отображение на , то:

1.  — корень;

2. итерационная последовательность 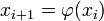 сходится к этому корню;

3. для очередного члена  справедливо 

Поясним смысл параметра . Согласно теореме Лагранжа имеем:

Отсюда следует, что . Таким образом, для сходимости метода достаточно, чтобы 

1. 

.........

и так далее, пока 

Применительно к СЛАУ

Рассмотрим систему:

Для неё итерационное вычисление будет выглядеть так:

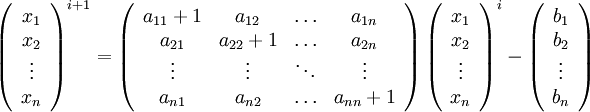
Сходимость метода будет осуществлять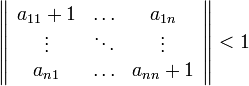 

Следует отметить, что для оценки сходимости вычисляется не определитель матрицы, а норма матрицы. Поэтому в данном случае поставлены двойные вертикальные черты, а не одинарные.

Решение уравнения cos(x)=x по методу простой итерации, очередная итерация: x_n+1=cos x_n, начальное приближение: x₁ = -1

Алгоритм

1. Условие  преобразуется к виду , где  — сжимающая

2. Задаётся начальное приближение и точность 

3. Вычисляется очередная итерация 

• Если , то  и возврат к шагу 3.

• Иначе  и остановка.

Практическая часть(выполнение в таблице Excel)

Для начала вручную выделим из уравнения х1,х2,х3,х4:

X1= (-91-2x₂+5x₃+3*x4)/8

X2= (-12+x₁+3*x3+2x₄)/(-7)

X3=(-60+8*x1-x₂)/(-9)

X4=(-43+5x1-3*x₂-5*x3)/(-9)

Воспользуемся таблицей Excel:

x1	x2	x3	x4	dx1	dx2	dx3	dx4	Dx
-91	-12	-60	-43	29	60,57143	127,1746	135,7319	135,7319
-62	48,57143	67,1746	92,73192	38,27646	87,81589	24,26619	5,473955	87,81589
-100,276	-39,2445	91,4408	98,20588	4,734867	12,64019	5,613236	9,962344	12,64019
-95,5416	-51,8847	85,82756	88,24353	10,4042	3,765742	8,829762	9,430287	10,4042
-85,1374	-48,1189	76,9978	78,81325	8,113524	5,319477	6,620968	6,41267	8,113524
-77,0239	-42,7994	70,37683	72,40058	5,212987	3,925037	4,197651	3,919787	5,212987
-71,8109	-38,8744	66,17918	68,48079	3,112193	2,474333	2,491468	2,288367	3,112193
-68,6987	-36,4001	63,68771	66,19242	1,796721	1,464916	1,434317	1,306716	1,796721
-66,902	-34,9351	62,2534	64,88571	1,020238	0,842307	0,813288	0,737857	1,020238
-65,8817	-34,0928	61,44011	64,14785	0,574425	0,477308	0,457566	0,414225	0,574425
-65,3073	-33,6155	60,98254	63,73362	0,321986	0,268452	0,256382	0,231832	0,321986
-64,9853	-33,3471	60,72616	63,50179	0,180063	0,150392	0,143345	0,12954	0,180063
-64,8053	-33,1967	60,58281	63,37225	0,10057	0,084078	0,080054	0,072321	0,10057
-64,7047	-33,1126	60,50276	63,29993	0,056135	0,046953	0,04468	0,040357	0,056135
-64,6485	-33,0657	60,45808	63,25957	0,031321	0,026205	0,024929	0,022515	0,031321
-64,6172	-33,0395	60,43315	63,23706	0,017473	0,014621	0,013907	0,01256	0,017473
-64,5998	-33,0248	60,41924	63,2245	0,009746	0,008156	0,007757	0,007005	0,009746
-64,59	-33,0167	60,41149	63,21749	0,005436	0,004549	0,004327	0,003907	0,005436
-64,5846	-33,0121	60,40716	63,21359	0,003032	0,002538	0,002413	0,002179	0,003032
-64,5815	-33,0096	60,40475	63,21141	0,001691	0,001415	0,001346	0,001216	0,001691
-64,5798	-33,0082	60,4034	63,21019	0,000943	0,000789	0,000751	0,000678	0,000943
-64,5789	-33,0074	60,40265	63,20951	0,000526	0,00044	0,000419	0,000378	0,000526
-64,5784	-33,0069	60,40223	63,20914	0,000293	0,000246	0,000234	0,000211	0,000293
-64,5781	-33,0067	60,402	63,20892	0,000164	0,000137	0,00013	0,000118	0,000164

Mетод Гаусса-Зейделя

Данная функция:

8x₁+2x₂-5x₃-3x₄=-91

-x₁-7x₂-3x₃-2x₄=-12

-8x₁+x₂-9x₃=-60

-5x₁+3x₂+5x₃-9x₄=-43

Теоретическая часть

Метод Гаусса—Зейделя является классическим итерационным методом решения системы линейных уравнений.

Постановка задачи

Возьмём систему: , где 

Или 

И покажем, как её можно решить с использованием метода Гаусса-Зейделя.

Метод

Чтобы пояснить суть метода, перепишем задачу в виде:

Здесь в -м уравнении мы перенесли в правую часть все члены, содержащие  , для . Эта запись может быть представлена:

где в принятых обозначениях  означает матрицу, у которой на главной диагонали стоят соответствующие элементы матрицы , а все остальные нули; тогда как матрицы  и содержат верхнюю и нижнюю треугольные части , на главной диагонали которых нули.

Итерационный процесс в методе Гаусса-Зейделя строится по формуле  после выбора соответствующего начального приближения .

Метод Гаусса-Зейделя можно рассматривать как модификацию метода Якоби. Основная идея модификации состоит в том, что новые значения  используются здесь сразу же по мере получения, в то время как в методе Якоби они не используются до следующей итерации:

где 

Таким образом, i-тая компонента -го приближения вычисляется по формуле:

Условие сходимости

Приведём достаточное условие сходимости метода.

Теорема. Пусть , где  – матрица, обратная к . Тогда при любом выборе начального приближения :

1. метод Гаусса-Зейделя сходится;

2. скорость сходимости метода равна скорости сходимости геометрической прогрессии со знаменателем ;

3. верна оценка погрешности: .

Условие окончания

Условие окончания итерационного процесса Зейделя при достижении точности  в упрощённой форме имеет вид:

Более точное условие окончания итерационного процесса имеет вид

и требует больше вычислений. Хорошо подходит для разреженных матриц.

Практическая часть (выполняется в таблице Excel)

Расчёт методом Гаусса-Зейдаля

Расчёт данного метода выполнялся в таблице Exel:

x1	x2	x3	x4	dx1	dx2	dx3	dx4	Dx
-91	-12	-60	-43	29	64,71429	146,2222	61	146,2222
-62	52,71429	86,22222	18	115,2407	97,42681	19,04762	74,73192	115,2407
53,24074	-44,7125	67,1746	92,73192	39,17308	6,49572	24,26619	5,473955	39,17308
92,41382	-51,2082	91,4408	98,20588	4,084103	4,575647	5,613236	9,962344	9,962344
88,32971	-46,6326	85,82756	88,24353	9,996395	4,992237	8,829762	9,430287	9,996395
78,33332	-41,6404	76,9978	78,81325	7,872725	3,510674	6,620968	6,41267	7,872725
70,46059	-38,1297	70,37683	72,40058	5,074711	2,17422	4,197651	3,919787	5,074711
65,38588	-35,9555	66,17918	68,48079	3,033888	1,276992	2,491468	2,288367	3,033888
62,35199	-34,6785	63,68771	66,19242	1,752696	0,73138	1,434317	1,306716	1,752696
60,5993	-33,9471	62,2534	64,88571	0,995578	0,41362	0,813288	0,737857	0,995578
59,60372	-33,5335	61,44011	64,14785	0,56064	0,232389	0,457566	0,414225	0,56064
59,04308	-33,3011	60,98254	63,73362	0,314289	0,130118	0,256382	0,231832	0,314289
58,72879	-33,171	60,72616	63,50179	0,175767	0,072722	0,143345	0,12954	0,175767
58,55303	-33,0982	60,58281	63,37225	0,098174	0,040605	0,080054	0,072321	0,098174
58,45485	-33,0576	60,50276	63,29993	0,054797	0,02266	0,04468	0,040357	0,054797
58,40005	-33,035	60,45808	63,25957	0,030575	0,012642	0,024929	0,022515	0,030575
58,36948	-33,0223	60,43315	63,23706	0,017057	0,007052	0,013907	0,01256	0,017057
58,35242	-33,0153	60,41924	63,2245	0,009514	0,003934	0,007757	0,007005	0,009514
58,34291	-33,0113	60,41149	63,21749	0,005307	0,002194	0,004327	0,003907	0,005307
58,3376	-33,0092	60,40716	63,21359	0,00296	0,001224	0,002413	0,002179	0,00296
58,33464	-33,0079	60,40475	63,21141	0,001651	0,000683	0,001346	0,001216	0,001651
58,33299	-33,0072	60,4034	63,21019	0,000921	0,000381	0,000751	0,000678	0,000921
58,33207	-33,0069	60,40265	63,20951	0,000514	0,000212	0,000419	0,000378	0,000514
58,33156	-33,0067	60,40223	63,20914	0,000286	0,000118	0,000234	0,000211	0,000286
58,33127	-33,0065	60,402	63,20892	0,00016	6,6E-05	0,00013	0,000118	0,00016
58,33111	-33,0065	60,40187	63,20881