
Demovariant
.docДемонстрационный вариант по математике (1курс 9,35,36 группы)
Решите задание, сравните полученный ответ с предложенными. Номер правильного ответа отметьте в бланке ответов под номером выполненного задания.
|
ЗАДАНИЯ |
ВАРИАНТЫ ОТВЕТОВ |
|
1.
Если
|
а) |
|
2.
Если
|
а)
5/2; б) 5/3; в)
|
|
3.
Скалярное произведение векторов
|
а)2; б) 0; в) 3; г) -2; д) 1 |
|
4.
Какие из векторов
|
а)
|
|
5.
Если
|
а) -8 б) -9 в) -10 г) -11 д) -12 |
|
6.
Один из фокусов эллипса
|
а) (4;0) б) (0;-4) в) (0;-3) г) (0;5) д) (-3;0) |
|
7.
Центр кривой
|
а) (0;-2) б) (0;1) в) (-2;0) г) (2;0) д) (1;0) |
|
8. Центр гиперболы совпадает с началом координат. Если ее фокус лежит в точке (2;0) и вершина в точке (-1;0), то уравнение гиперболы имеет вид |
а) 3х2-2у2=3 б) х2-2у2=1 в) 2х2-3у2=2 г) х2-3у2=1 д) 3х2-у2=3 |
|
9. Функция ƒ определена на всей числовой прямой. Если существует С<0 такое, что для любого х выполняется неравенство ƒ(х)<С, то ƒ обязательно |
а) положительна б) ограничена в) убывает г) отрицательна д) неограничена |
|
10.
Предел последовательности
|
а) 3 б) 2 в) 1,5 г) 0 д) 0,5 |
|
11.
Значение
|
а)-1/2; б) 3/2; в) 1/2; г) 1; д) 0 |
|
12.
Значение
|
а)
-1 б) - |
|
13.
Значение
|
а)0,5 б)0,75 в)1 г)1,5 д)2,5 |
|
14.
Функция ƒ(х)= |
а) -3 б) 3 в) 0 г) 5 д) -5 |
|
15. Уравнение касательной к линии у=·х3+3х2-5 и перпендикулярной прямой 2х-6у+1=0 имеет вид |
а)
г)
у= |
|
16.
Результатом вычисления
|
а)
в)
|
|
17.
Значение производной функции
|
а)
0
б)
|
|
18.
Производная
|
а)
|
|
19.
Уравнение наклонной асимптоты графика
функ–ции
|
а) у=-5х+2 б) у=5х-2 в) у=5х-1 г) у=-5х+1 д) у=5х-3 |
|
20.
Функция
|
а)
(- |
|
21.
Число точек экстремума функции
|
а) 2 б) 3 в) 1 г) 0 д) 4 |
|
22.
Интеграл
|
а) |
|
23.
Одна из первообразных для функции
|
а) |
|
24. Одна из первообразных для функции x·cos(x2 +3) имеет вид |
а)
в)
|
|
25.
Если F(x)
– первообразная для функции
(2х-5) |
а)
г)
|
|
26.
Если F(x)
–
первообразная функции
|
а)
1
б) - |
|
2 |
а) |
|
28.
Если график первообразной F(x)
для функции
|
а)2+2ln15
б)2–ln45
в)4+ln48
г)4-ln |
|
29.
Значение интеграла
|
а)
2 б) 1 в)
|
|
30.
Значение
интеграла
|
а)
|
|
31.
Значение
интеграла
|
а) ln2 б) ln4-1 в) ln4 г) ln2+1 д) 2ln2+1 |
|
32. Площадь фигуры, ограниченной графиками функций у=(х-2)2 и у=х-2, равна |
а)
г)
|
|
33.
Вычисление несобственного интеграла
|
а) интеграл
расходится б) I=0 в) I=
г) I= |
|
34. Объем тетраэдра с вершинами А(4;3;0), В(-1;2;1), С(3;4;1) и D(5;6;2) равен |
а)
|

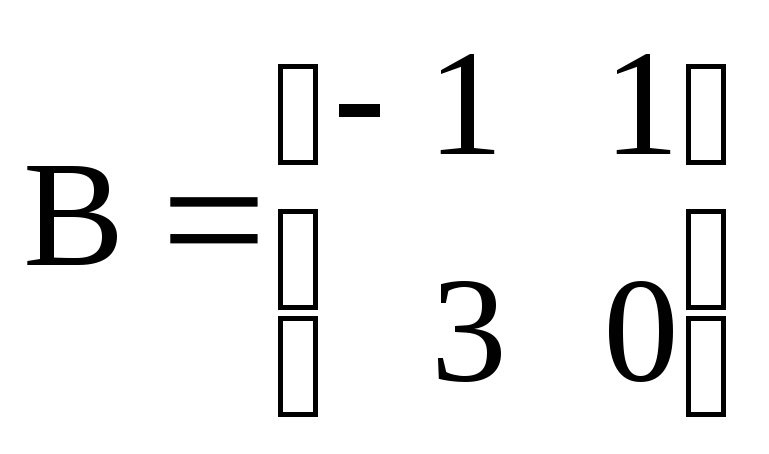 ,
то A+3B=...
,
то A+3B=...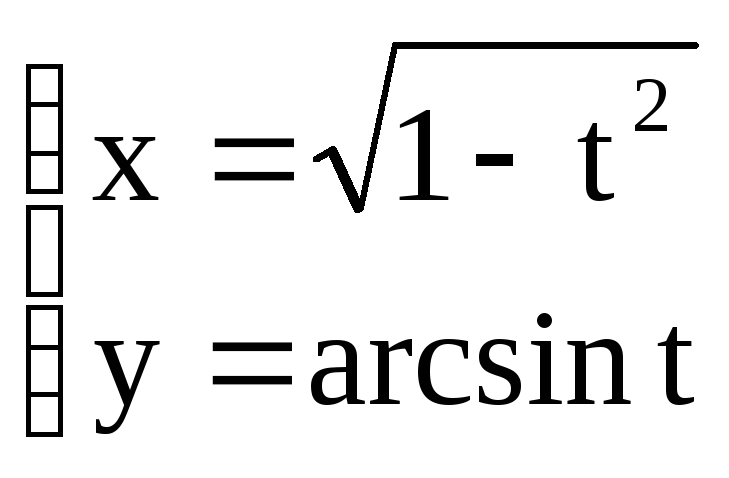 ,
заданной параметрически, равна
,
заданной параметрически, равна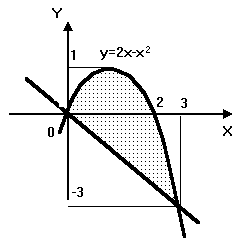 7.
Какой из следующих интегралов
представляет площадь заштрихованной
части фигуры, изображенной на чертеже?
7.
Какой из следующих интегралов
представляет площадь заштрихованной
части фигуры, изображенной на чертеже?